Эффективная (и хорошо объясненная) реализация Quadtree для 2D обнаружения столкновений
Я работал над добавлением Quadtree в программу, которую я пишу, и я не могу не заметить, что есть несколько хорошо объясненных / выполняющих обучающих программ для реализации, которую я ищу.
В частности, я ищу список методов и псевдокодов для их реализации (или просто описание их процессов), которые обычно используются в Quadtree (извлечение, вставка, удаление и т. Д.), А также может быть, несколько советов по улучшению производительности. Это для обнаружения столкновений, поэтому лучше всего объяснить их с помощью 2d прямоугольников, поскольку они являются объектами, которые будут сохранены.
7 ответов
1. Эффективное дерево
Хорошо, я сделаю снимок. Сначала тизер, чтобы показать результаты того, что я предложу, с участием 20000 агентов (просто кое-что, что я очень быстро взялся за этот конкретный вопрос):
GIF имеет чрезвычайно уменьшенную частоту кадров и значительно более низкое разрешение, чтобы соответствовать максимуму 2 МБ для этого сайта. Вот видео, если вы хотите увидеть его практически на полной скорости: https://streamable.com/3pgmn.
И GIF с 100k, хотя мне пришлось так много возиться с ним, и мне пришлось отключить линии дерева квадрантов (кажется, не хотелось слишком сильно их сжимать), а также изменить способ, которым агенты выглядели, чтобы получить его. вписывается в 2 мегабайта (хотелось бы, чтобы GIF был так же прост, как и кодирование дерева квадрантов):
Симуляция с агентами 20k занимает ~3 мегабайта оперативной памяти. Я также могу легко работать с агентами на 100000 меньших размеров, не жертвуя частотой кадров, хотя это приводит к небольшому беспорядку на экране до такой степени, что вы едва можете видеть, что происходит, как в GIF выше. Все это выполняется в одном потоке на моем i7, и я трачу почти половину времени в соответствии с VTune, просто рисуя этот материал на экране (просто используя некоторые базовые скалярные инструкции, чтобы отобразить объекты по одному пикселю за раз в CPU).
А вот видео с 100000 агентов, хотя трудно понять, что происходит. Это своего рода большое видео, и я не смог найти достойного способа сжать его без превращения всего видео в кашу (может потребоваться сначала загрузить или кэшировать его, чтобы увидеть поток с разумным FPS). С агентами по 100 тысяч симуляций требуется около 4,5 мегабайт оперативной памяти, и использование памяти остается очень стабильным после выполнения симуляции в течение примерно 5 секунд (прекращается повышение или понижение, поскольку оно перестает выделять кучу). То же самое в замедленном движении.
Эффективное Quadtree для обнаружения столкновений
Хорошо, так что на самом деле квадродерево не моя любимая структура данных для этой цели. Я предпочитаю предпочитать иерархию сеток, например, грубую сетку для мира, более мелкую сетку для региона и еще более мелкую сетку для субрегиона (3 фиксированных уровня плотных сеток и без деревьев), с рядными основанные на оптимизации, так что строка, в которой нет сущностей, будет освобождена и превращена в нулевой указатель, а также полностью пустые области или подобласти превращены в нули. Хотя эта простая реализация квадродерева, работающего в одном потоке, может обрабатывать 100 тыс. Агентов на моем i7 со скоростью более 60 FPS, я реализовал сетки, которые могут обрабатывать пару миллионов агентов, отскакивающих друг от друга каждый кадр на более старом оборудовании (i3). Также мне всегда нравилось, как сетки позволяют очень легко предсказать, сколько памяти им потребуется, поскольку они не разделяют ячейки. Но я попытаюсь осветить, как реализовать достаточно эффективное квадродерево.
Обратите внимание, что я не буду вдаваться в полную теорию структуры данных. Я предполагаю, что вы уже знаете это и заинтересованы в повышении производительности. Я также просто вхожу в свой личный способ решения этой проблемы, который, кажется, превосходит большинство решений, которые я нахожу онлайн для своих случаев, но есть много достойных способов, и эти решения адаптированы к моим случаям использования (очень большие входы все движется каждый кадр для визуального FX в фильмах и на телевидении). Другие люди, вероятно, оптимизируют для различных случаев использования. Когда речь идет, в частности, о структурах пространственной индексации, я действительно думаю, что эффективность решения говорит вам больше об исполнителе, чем о структуре данных. Также те же стратегии, которые я предлагаю ускорить, также применимы в трех измерениях с октреями.
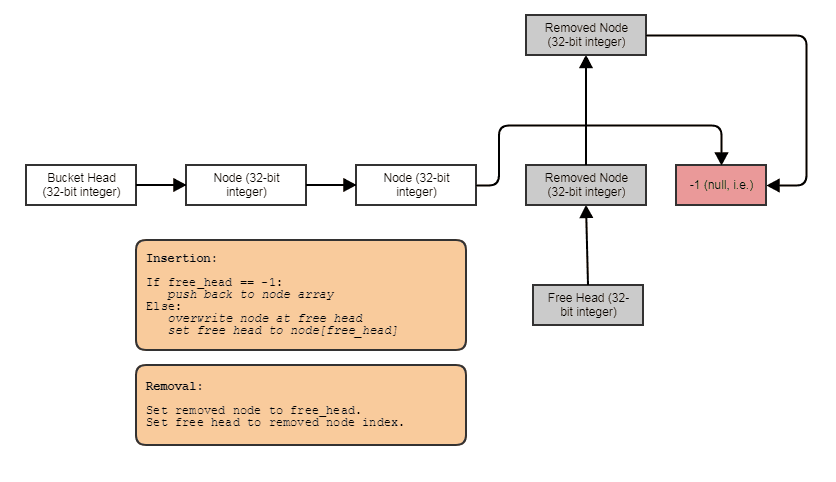
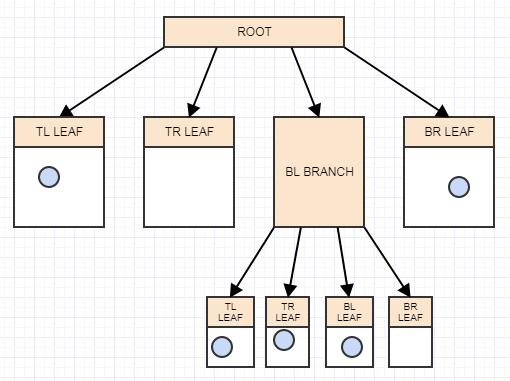
Представление узла
Итак, прежде всего, давайте рассмотрим представление узла:
// Represents a node in the quadtree.
struct QuadNode
{
// Points to the first child if this node is a branch or the first
// element if this node is a leaf.
int32_t first_child;
// Stores the number of elements in the leaf or -1 if it this node is
// not a leaf.
int32_t count;
};
Это всего 8 байтов, и это очень важно, так как это ключевая часть скорости. На самом деле я использую меньший (6 байт на узел), но я оставлю это в качестве упражнения для читателя.
Вы, вероятно, можете обойтись без count, Я включил это для патологических случаев, чтобы избежать линейного обхода элементов и подсчета их каждый раз, когда листовой узел может разделиться. В большинстве общих случаев узел не должен хранить столько элементов. Тем не менее, я работаю в визуальном FX, и патологические случаи не обязательно редки. Вы можете встретить художников, создающих контент с кучей совпадающих точек, массивных полигонов, которые охватывают всю сцену, и т. Д., Поэтому я в конечном итоге храню count,
Где AABB?
Таким образом, первое, что может заинтересовать людей, это то, где ограничительные рамки (прямоугольники) предназначены для узлов. Я не храню их. Я вычисляю их на лету. Я немного удивлен, что большинство людей не делают этого в коде, который я видел. Для меня они хранятся только с древовидной структурой (в основном только одна AABB для корня).
Может показаться, что было бы дороже вычислять их на лету, но сокращение использования памяти узлом может пропорционально уменьшить количество кеш-пропусков при обходе дерева, и эти сокращения пропусков кеш-памяти имеют тенденцию быть более значительными, чем необходимость сделать несколько битовых сдвигов и некоторые сложения / вычитания во время обхода. Обход выглядит так:
static QuadNodeList find_leaves(const Quadtree& tree, const QuadNodeData& root, const int rect[4])
{
QuadNodeList leaves, to_process;
to_process.push_back(root);
while (to_process.size() > 0)
{
const QuadNodeData nd = to_process.pop_back();
// If this node is a leaf, insert it to the list.
if (tree.nodes[nd.index].count != -1)
leaves.push_back(nd);
else
{
// Otherwise push the children that intersect the rectangle.
const int mx = nd.crect[0], my = nd.crect[1];
const int hx = nd.crect[2] >> 1, hy = nd.crect[3] >> 1;
const int fc = tree.nodes[nd.index].first_child;
const int l = mx-hx, t = my-hx, r = mx+hx, b = my+hy;
if (rect[1] <= my)
{
if (rect[0] <= mx)
to_process.push_back(child_data(l,t, hx, hy, fc+0, nd.depth+1));
if (rect[2] > mx)
to_process.push_back(child_data(r,t, hx, hy, fc+1, nd.depth+1));
}
if (rect[3] > my)
{
if (rect[0] <= mx)
to_process.push_back(child_data(l,b, hx, hy, fc+2, nd.depth+1));
if (rect[2] > mx)
to_process.push_back(child_data(r,b, hx, hy, fc+3, nd.depth+1));
}
}
}
return leaves;
}
Пропуск AABB - одна из самых необычных вещей, которые я делаю (я продолжаю искать других людей, делающих это просто для того, чтобы найти сверстника и потерпеть неудачу), но я измерил до и после, и это значительно сократило время, по крайней мере, на очень большие входы, чтобы существенно уплотнить узел дерева квадрантов и просто вычислять AABB на лету во время обхода. Пространство и время не всегда диаметрально противоположны. Иногда сокращение пространства также означает сокращение времени, учитывая, насколько производительность сегодня доминирует в иерархии памяти. Я даже ускорил некоторые реальные операции, применяемые к массивным входам, сжимая данные, чтобы в четыре раза использовать память, и распаковывать на лету.
Я не знаю, почему многие люди предпочитают кэшировать AABB: удобство программирования или действительно быстрое в их случаях. Тем не менее, для структур данных, которые равномерно распределяются по центру, как обычные квадри и октре, я бы рекомендовал измерить влияние исключения AABB и вычислить их на лету. Вы можете быть очень удивлены. Конечно, имеет смысл хранить AABB для структур, которые не разделяются равномерно, как Kd-деревья и BVH, а также для свободных четырех деревьев.
Плавающая запятая
Я не использую плавающую точку для пространственных индексов, и, возможно, именно поэтому я вижу улучшенную производительность, просто вычисляя AABB на лету с правыми сдвигами для деления на 2 и так далее. Тем не менее, по крайней мере, SPFP кажется очень быстрым в наши дни. Я не знаю, так как я не измерил разницу. Я просто использую целые числа по предпочтению, хотя я обычно работаю с входными данными с плавающей точкой (вершины сетки, частицы и т. Д.). Я просто в конечном итоге преобразую их в целочисленные координаты с целью разделения и выполнения пространственных запросов. Я не уверен, есть ли какое-то существенное преимущество в скорости от этого. Это просто привычка и предпочтение, так как мне проще рассуждать о целых числах, не думая о денормализованном FP и всем этом.
Центрированные AABB
Хотя я сохраняю ограничивающий прямоугольник только для корня, он помогает использовать представление, в котором хранятся центр и половинный размер для узлов, в то время как представление запросов влево / верх / право / низ для запросов сводит к минимуму количество задействованной арифметики.
Смежные дети
Это также ключ, и если мы вернемся к узлу rep:
struct QuadNode
{
int32_t first_child;
...
};
Нам не нужно хранить массив дочерних элементов, потому что все 4 дочерних элемента являются смежными:
first_child+0 = index to 1st child (TL)
first_child+1 = index to 2nd child (TR)
first_child+2 = index to 3nd child (BL)
first_child+3 = index to 4th child (BR)
Это не только значительно уменьшает потери в кеше при обходе, но также позволяет нам значительно сократить наши узлы, что еще больше уменьшает потери в кеше, сохраняя только один 32-битный индекс (4 байта) вместо массива 4 (16 байтов).
Это означает, что если вам нужно передать элементы только в пару квадрантов родительского элемента при его разбиении, он все равно должен выделить все 4 дочерних листа для хранения элементов только в двух квадрантах, в то время как два пустых листа будут дочерними. Тем не менее, компромисс более чем оправдан с точки зрения производительности, по крайней мере, в моих случаях использования, и помните, что узел занимает всего 8 байтов, учитывая, сколько мы его уплотнили.
Освобождая детей, мы освобождаем всех четверых за раз. Я делаю это в постоянном времени, используя индексированный свободный список, например так:
За исключением того, что мы объединяем фрагменты памяти, содержащие 4 смежных элемента вместо одного за раз. Это делает его таким, что нам обычно не нужно задействовать какие-либо выделения кучи или освобождения во время моделирования. Группа из 4 узлов помечается как освобождаемая неделимо только для того, чтобы затем восстанавливаться неделимо в последующем разделении другого конечного узла.
Отложенная очистка
Я не обновляю структуру quadtree сразу после удаления элементов. Когда я удаляю элемент, я просто спускаюсь вниз по дереву к дочернему узлу (ам), который он занимает, а затем удаляю элемент, но я не потрудился сделать что-то еще, даже если листья стали пустыми.
Вместо этого я делаю отложенную очистку следующим образом:
void Quadtree::cleanup()
{
// Only process the root if it's not a leaf.
SmallList<int> to_process;
if (nodes[0].count == -1)
to_process.push_back(0);
while (to_process.size() > 0)
{
const int node_index = to_process.pop_back();
QuadNode& node = nodes[node_index];
// Loop through the children.
int num_empty_leaves = 0;
for (int j=0; j < 4; ++j)
{
const int child_index = node.first_child + j;
const QuadNode& child = nodes[child_index];
// Increment empty leaf count if the child is an empty
// leaf. Otherwise if the child is a branch, add it to
// the stack to be processed in the next iteration.
if (child.count == 0)
++num_empty_leaves;
else if (child.count == -1)
to_process.push_back(child_index);
}
// If all the children were empty leaves, remove them and
// make this node the new empty leaf.
if (num_empty_leaves == 4)
{
// Push all 4 children to the free list.
nodes[node.first_child].first_child = free_node;
free_node = node.first_child;
// Make this node the new empty leaf.
node.first_child = -1;
node.count = 0;
}
}
}
Это вызывается в конце каждого кадра после перемещения всех агентов. Причина, по которой я делаю этот вид отложенного удаления пустых конечных узлов в нескольких итерациях, а не все сразу в процессе удаления одного элемента, заключается в том, что этот элемент A может перейти к узлу N2, делая N1 пустой. Тем не менее, элемент B может в том же кадре перейти к N1 Занять его снова.
С помощью отложенной очистки мы можем обрабатывать такие случаи, не удаляя ненужных потомков, а только добавлять их обратно, когда другой элемент перемещается в этот сектор.
Перемещение элементов в моем случае является простым: 1) удалить элемент, 2) переместить его, 3) повторно вставить его в дерево квадрантов. После того, как мы переместим все элементы и в конце кадра (не временной шаг, может быть несколько временных шагов на кадр), cleanup Вышеприведенная функция вызывается для удаления потомков от родителя, у которого 4 пустых листа в качестве потомков, что фактически превращает этого родителя в новый пустой лист, который затем может быть очищен в следующем кадре с последующим cleanup call (или нет, если что-то вставлено в него или если родные братья пустого листа не пустые).
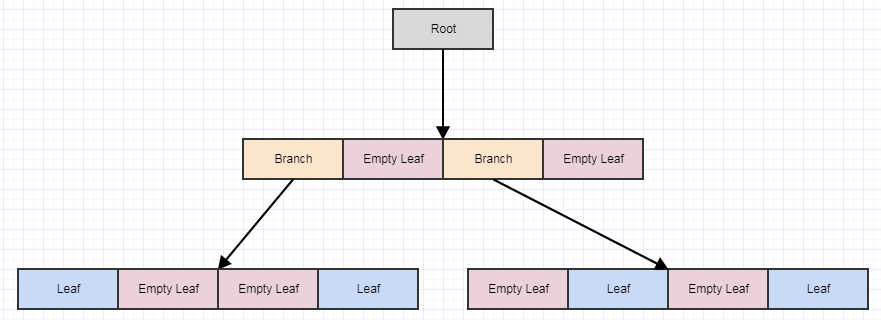
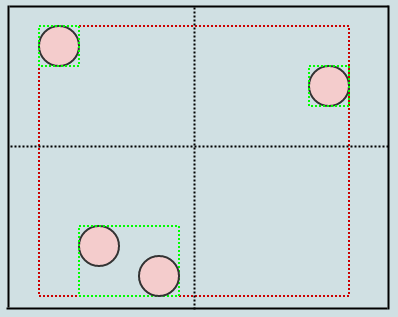
Давайте посмотрим на отложенную очистку визуально:
Начнем с этого, скажем, мы удалили некоторые элементы из дерева, оставив нам 4 пустых листа:
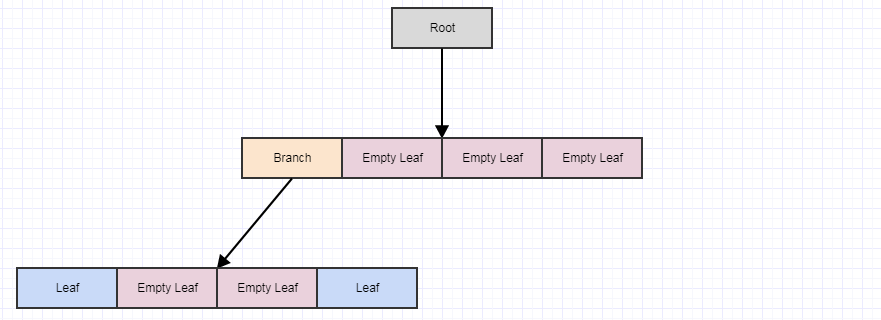
На данный момент, если мы позвоним cleanup, он удалит 4 листа, если найдет 4 пустых дочерних листа и превратит родителя в пустой лист, вот так:
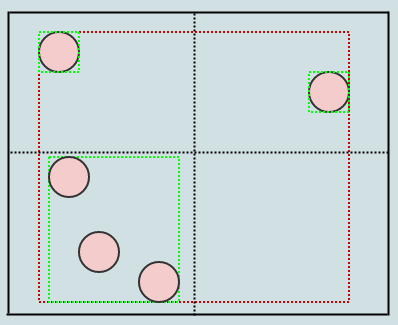
Допустим, мы удалили еще несколько элементов:
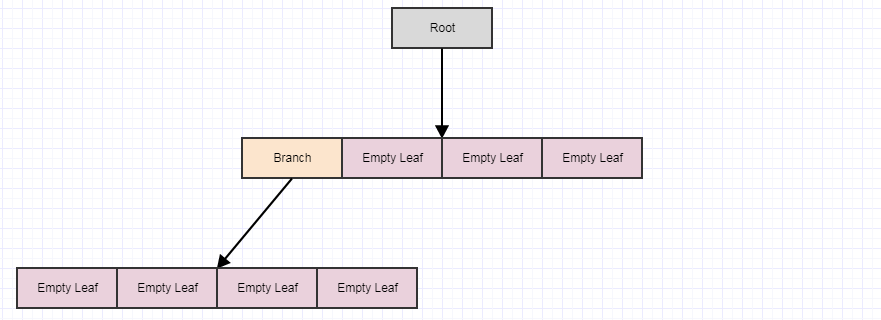
... а затем позвоните cleanup снова:
Если мы позвоним еще раз, мы получим следующее:
... в этот момент сам корень превращается в пустой лист. Однако метод очистки никогда не удаляет рут (он удаляет только дочерние элементы). Опять же, основной смысл сделать это отложенным таким образом и в несколько этапов - уменьшить количество потенциальной избыточной работы, которая может произойти за шаг по времени (что может быть много), если бы мы делали все это сразу же каждый раз, когда элемент удаляется из дерево. Это также помогает распределить это по кадрам, чтобы избежать заиканий.
TBH, я первоначально применил эту технику "отложенной очистки" в игре для DOS, которую я написал на C из-за чистой лени! Я не хотел беспокоиться о спуске вниз по дереву, удалении элементов, а затем об удалении узлов восходящим способом, потому что изначально я писал дерево для поддержки обхода сверху вниз (не сверху вниз и снова вверх) и действительно думал, что это ленивое решение было компромиссом производительности (жертвуя оптимальной производительностью, чтобы быть реализованным быстрее). Однако, много лет спустя, я фактически нашел способ реализовать удаление дерева квадратов способами, которые немедленно начали удалять узлы, и, к моему удивлению, я фактически значительно замедлил его с более непредсказуемыми и падающими частотами кадров. Отложенная очистка, несмотря на то, что изначально она была вдохновлена моей ленью программиста, была фактически (и случайно) очень эффективной оптимизацией для динамических сцен.
Односвязные индексы для элементов
Для элементов я использую это представление:
// Represents an element in the quadtree.
struct QuadElt
{
// Stores the ID for the element (can be used to
// refer to external data).
int id;
// Stores the rectangle for the element.
int x1, y1, x2, y2;
};
// Represents an element node in the quadtree.
struct QuadEltNode
{
// Points to the next element in the leaf node. A value of -1
// indicates the end of the list.
int next;
// Stores the element index.
int element;
};
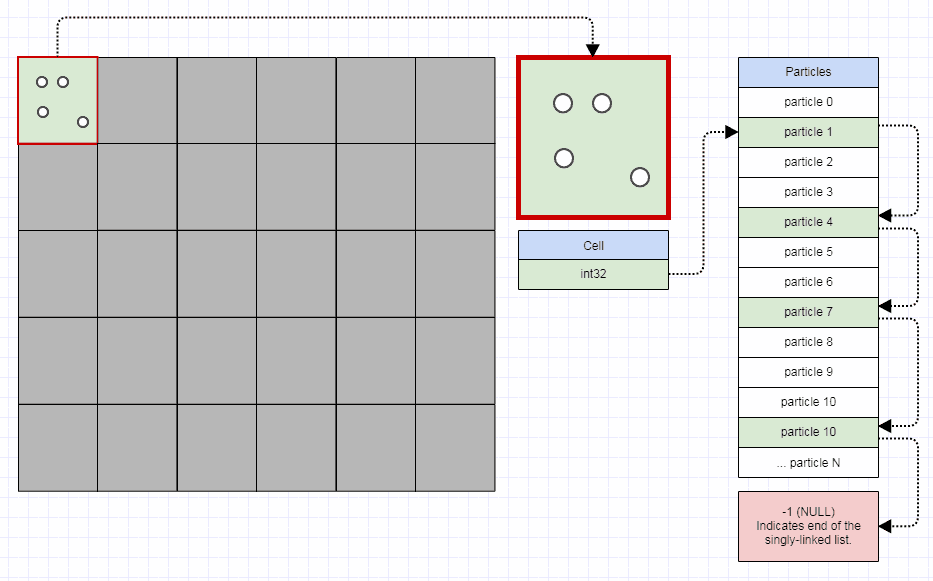
Я использую "элементный узел", который отделен от "элемента". Элемент вставляется в квадродерево только один раз, независимо от того, сколько ячеек он занимает. Однако для каждой ячейки, которую он занимает, вставляется "узел элемента", который индексирует этот элемент.
Узел элемента является узлом списка индексов с односвязной связью в массиве, а также с использованием метода свободного списка выше. Это приводит к еще большему количеству промахов кэша при хранении всех элементов, смежных для листа. Однако, учитывая, что это квадродерево предназначено для очень динамических данных, которые перемещаются и сталкиваются на каждом временном шаге, обычно требуется больше времени на обработку, чем экономится, чтобы найти идеально непрерывное представление для конечных элементов (вам бы фактически пришлось реализовать переменную распределитель памяти, который очень быстр, и это далеко не так просто). Поэтому я использую односвязный индексный список, который позволяет свободный список подходов распределения / освобождения в постоянное время. Когда вы используете это представление, вы можете перенести элементы из разделенных родителей в новые листья, просто изменив несколько целых чисел.
SmallList<T>
О, я должен упомянуть об этом. Естественно, это помогает, если вы не выделяете кучу просто для хранения временного стека узлов для нерекурсивного обхода. SmallList<T> похож на vector<T> за исключением того, что он не будет включать выделение кучи, пока вы не вставите в него более 128 элементов. Это похоже на строковую оптимизацию SBO в стандартной библиотеке C++. Это то, что я реализовал и использовал целую вечность, и это очень помогает убедиться, что вы используете стек когда бы ни было возможно.
Представление дерева
Вот представление самого quadtree:
struct Quadtree
{
// Stores all the elements in the quadtree.
FreeList<QuadElt> elts;
// Stores all the element nodes in the quadtree.
FreeList<QuadEltNode> elt_nodes;
// Stores all the nodes in the quadtree. The first node in this
// sequence is always the root.
std::vector<QuadNode> nodes;
// Stores the quadtree extents.
QuadCRect root_rect;
// Stores the first free node in the quadtree to be reclaimed as 4
// contiguous nodes at once. A value of -1 indicates that the free
// list is empty, at which point we simply insert 4 nodes to the
// back of the nodes array.
int free_node;
// Stores the maximum depth allowed for the quadtree.
int max_depth;
};
Как указано выше, мы храним один прямоугольник для корня (root_rect). Все суб-ректы вычисляются на лету. Все узлы хранятся в непрерывном массиве (std::vector<QuadNode>) вместе с элементами и узлами элементов (в FreeList<T>).
FreeList<T>
Я использую FreeList структура данных, которая в основном является массивом (и последовательностью произвольного доступа), которая позволяет вам удалять элементы из любого места в постоянном времени (оставляя дыры, которые освобождаются после последующих вставок в постоянном времени) Вот упрощенная версия, которая не заботится об обработке нетривиальных типов данных (не использует размещение новых вызовов или вызовов ручного уничтожения):
/// Provides an indexed free list with constant-time removals from anywhere
/// in the list without invalidating indices. T must be trivially constructible
/// and destructible.
template <class T>
class FreeList
{
public:
/// Creates a new free list.
FreeList();
/// Inserts an element to the free list and returns an index to it.
int insert(const T& element);
// Removes the nth element from the free list.
void erase(int n);
// Removes all elements from the free list.
void clear();
// Returns the range of valid indices.
int range() const;
// Returns the nth element.
T& operator[](int n);
// Returns the nth element.
const T& operator[](int n) const;
private:
union FreeElement
{
T element;
int next;
};
std::vector<FreeElement> data;
int first_free;
};
template <class T>
FreeList<T>::FreeList(): first_free(-1)
{
}
template <class T>
int FreeList<T>::insert(const T& element)
{
if (first_free != -1)
{
const int index = first_free;
first_free = data[first_free].next;
data[index].element = element;
return index;
}
else
{
FreeElement fe;
fe.element = element;
data.push_back(fe);
return static_cast<int>(data.size() - 1);
}
}
template <class T>
void FreeList<T>::erase(int n)
{
data[n].next = first_free;
first_free = n;
}
template <class T>
void FreeList<T>::clear()
{
data.clear();
first_free = -1;
}
template <class T>
int FreeList<T>::range() const
{
return static_cast<int>(data.size());
}
template <class T>
T& FreeList<T>::operator[](int n)
{
return data[n].element;
}
template <class T>
const T& FreeList<T>::operator[](int n) const
{
return data[n].element;
}
У меня есть один, который работает с нетривиальными типами и предоставляет итераторы и так далее, но гораздо более сложный. В наши дни я склонен больше работать с тривиально конструируемыми / разрушаемыми структурами в стиле C (так или иначе, используя только нетривиальные пользовательские типы для высокоуровневых вещей).
Максимальная глубина дерева
Я предотвращаю слишком большое деление дерева, указав максимально допустимую глубину. Для быстрого моделирования, которое я набрал, я использовал 8. Для меня это очень важно, поскольку в VFX я часто сталкиваюсь с патологическими случаями, включая контент, созданный художниками с множеством совпадающих или перекрывающихся элементов, которые без ограничения максимальной глубины дерева могли бы хочу его подразделять на неопределенное время.
Есть небольшая настройка, если вы хотите добиться оптимальной производительности с учетом максимально допустимой глубины и количества элементов, которые вы можете сохранить в листе, прежде чем он разделится на 4 дочерних элемента. Я склоняюсь к тому, что оптимальные результаты достигаются при максимальном размере около 8 элементов на узел до его разделения, а также максимальной глубине, устанавливаемой таким образом, чтобы наименьший размер ячейки был немного больше размера вашего среднего агента (в противном случае можно было бы вставить больше отдельных агентов). в несколько листьев).
Столкновение и Запросы
Существует несколько способов обнаружения коллизий и запросов. Я часто вижу, как люди делают это так:
for each element in scene:
use quad tree to check for collision against other elements
Это очень просто, но проблема с этим подходом заключается в том, что первый элемент сцены может находиться в совершенно другом месте в мире, чем второй. В результате пути, по которым мы идем вниз по дереву, могут быть совершенно случайными. Мы могли бы пройти один путь к листу, а затем захотеть пойти по тому же пути снова для первого элемента, как, скажем, 50000-й элемент. К этому времени узлы, участвующие в этом пути, возможно, уже были удалены из кэша ЦП. Поэтому я рекомендую сделать это следующим образом:
traversed = {}
gather quadtree leaves
for each leaf in leaves:
{
for each element in leaf:
{
if not traversed[element]:
{
use quad tree to check for collision against other elements
traversed[element] = true
}
}
}
Хотя это немного больше кода и требует от нас traversed Битовый или параллельный массив некоторого вида, чтобы избежать обработки элементов дважды (поскольку они могут быть вставлены в более чем один лист), это помогает убедиться, что мы спускаемся по одним и тем же путям вниз по дереву по всему циклу. Это помогает сделать вещи более кэш-дружественными. Также, если после попытки переместить элемент на временном шаге, он все еще полностью охватывается в этом листовом узле, нам даже не нужно возвращаться обратно из корня (мы можем просто проверить только этот один лист).
Распространенные недостатки: что следует избегать
Несмотря на то, что существует множество способов избавиться от кошки и достичь эффективного решения, существует общий способ достижения очень неэффективного решения. И я столкнулся с моей долей очень неэффективных квадродерев, деревьев кд и октре в моей карьере, работая в VFX. Мы говорим о гигабайте памяти, используемой только для разбиения сетки на 100000 треугольников, при этом на сборку уходит 30 секунд, когда приличная реализация должна уметь делать то же самое сотни раз в секунду и всего несколько мегабайт. Есть много людей, которые разбираются с ними, чтобы решить проблемы, которые являются теоретиками, но не уделяют много внимания эффективности памяти.
Таким образом, самое распространенное "нет-нет", которое я вижу, - это хранить один или несколько полноценных контейнеров с каждым узлом дерева. Под полноценным контейнером я подразумеваю то, что владеет, выделяет и освобождает собственную память, например:
struct Node
{
...
// Stores the elements in the node.
List<Element> elements;
};
А также List<Element> может быть список в Python, ArrayList в Java или C#, std::vector в C++ и т.д.: некоторая структура данных, которая управляет собственной памятью / ресурсами.
Проблема здесь заключается в том, что, хотя такие контейнеры очень эффективно реализованы для хранения большого количества элементов, все они на всех языках крайне неэффективны, если вы создаете множество из них только для хранения нескольких элементов в каждом. Одна из причин заключается в том, что метаданные контейнера имеют тенденцию быть довольно взрывоопасными при использовании памяти на таком гранулярном уровне одного узла дерева. Контейнеру может понадобиться хранить размер, емкость, указатель / ссылку на данные, которые он выделяет и т. Д., И все это для обобщенной цели, поэтому он может использовать 64-разрядные целые числа для размера и емкости. В результате метаданные только для пустого контейнера могут составлять 24 байта, что уже в 3 раза больше, чем полное представление узла, которое я предложил, и это только для пустого контейнера, предназначенного для хранения элементов в листьях.
Кроме того, каждому контейнеру часто требуется либо выделить кучу /GC при вставке, либо заранее потребовать еще больше предварительно выделенной памяти (в этот момент для самого контейнера может потребоваться 64 байта). Так что это либо становится медленным из-за всех распределений (обратите внимание, что выделение GC вначале действительно быстрое в некоторых реализациях, таких как JVM, но это только для начального цикла Eden), либо из-за того, что мы загружаемся из-за пропусков кэша, потому что узлы настолько огромные, что едва ли вписываются в нижние уровни кэша ЦП при прохождении или оба.
Тем не менее, это очень естественный наклон и имеет интуитивный смысл, поскольку мы говорим об этих структурах теоретически, используя язык, такой как "Элементы хранятся в листьях", который предлагает хранить контейнер элементов в листовых узлах. К сожалению, это требует огромных затрат на использование и обработку памяти. Так что избегайте этого, если хотите создать что-то достаточно эффективное. Сделать Node совместно использовать и указывать (ссылаться) или индексировать память, выделенную и сохраненную для всего дерева, а не для каждого отдельного узла. В действительности элементы не должны храниться в листьях.
Элементы должны храниться в дереве, а конечные узлы должны индексировать или указывать на эти элементы.
Заключение
Фуф, так вот, что я делаю, чтобы достичь того, что, как мы надеемся, считается достойным решением. Надеюсь, это поможет. Обратите внимание, что я нацеливаю это на несколько продвинутый уровень для людей, которые уже внедрили квадри как минимум один или два раза. Если у вас есть какие-либо вопросы, не стесняйтесь стрелять.
Так как этот вопрос немного широк, я мог бы прийти и отредактировать его, и продолжать его дорабатывать и расширять, если он не закрывается (мне нравятся эти типы вопросов, поскольку они дают нам повод написать о нашем опыте работы в поле, но сайт не всегда их любит). Я также надеюсь, что некоторые эксперты могут использовать альтернативные решения, на которых я могу учиться и, возможно, использовать их для дальнейшего совершенствования.
Опять же, квадродерево на самом деле не моя любимая структура данных для таких чрезвычайно динамичных сценариев столкновений, как этот. Так что у меня, вероятно, есть кое-что, чему можно научиться у людей, которые предпочитают для этого quadtree и годами настраивали и настраивали их. В основном я использую квадри для статических данных, которые не перемещаются по каждому кадру, а для тех, что я использую, совсем другое представление, чем предложенное выше.
2. Основы
Для этого ответа (извините, я снова исчерпал лимит персонажей), я сосредоточусь больше на основах, нацеленных на кого-то новичка в этих структурах.
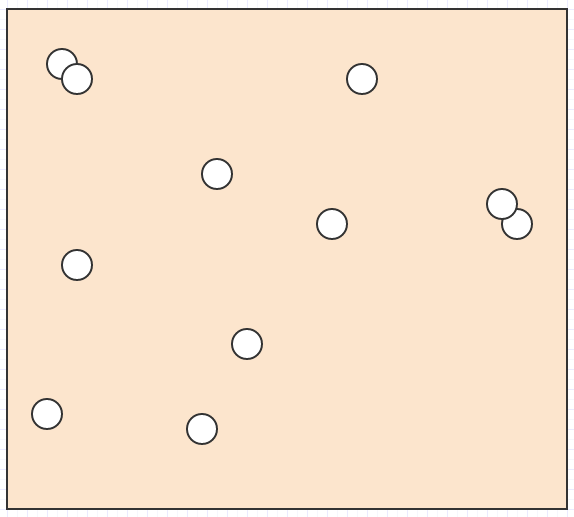
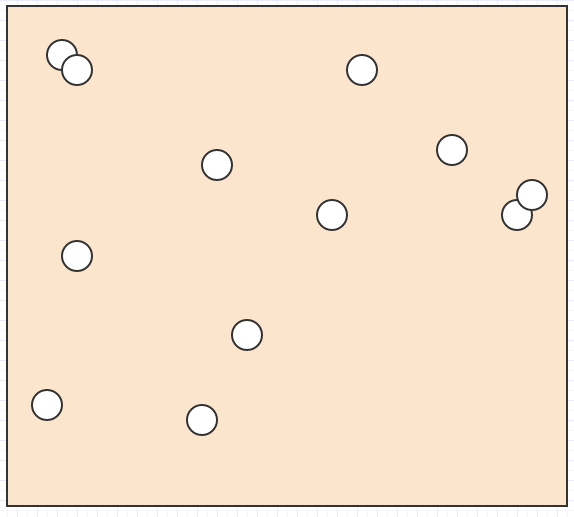
Хорошо, так скажем, у нас есть куча таких элементов в космосе:
И мы хотим выяснить, какой элемент находится под курсором мыши, или какие элементы пересекаются / сталкиваются друг с другом, или каков ближайший элемент к другому элементу, или что-то в этом роде.
В этом случае, если бы единственными данными, которые у нас были, были наборы положений и размеров / радиусов элементов в пространстве, нам пришлось бы пройтись по всему циклу, чтобы выяснить, какой элемент находится в данной области поиска. Для обнаружения столкновений мы должны были бы пройти через каждый отдельный элемент, а затем, для каждого элемента, пройти через все другие элементы, что делает его алгоритмом взрывной квадратичной сложности. Это не собирается придерживаться нетривиальных размеров ввода.
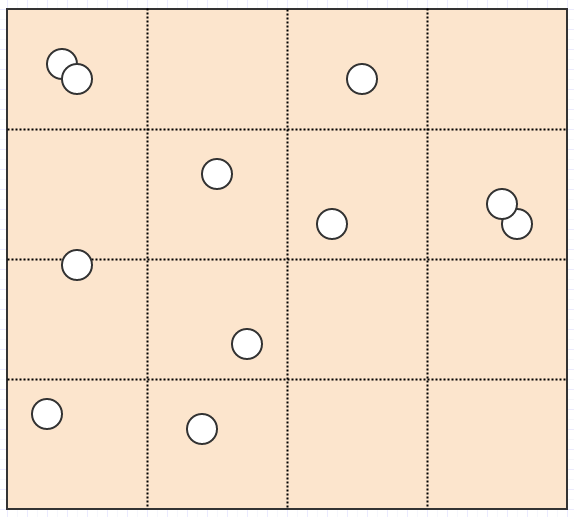
подразделять
Так что мы можем сделать с этой проблемой? Одним из простых подходов является подразделение пространства поиска (например, экрана) на фиксированное количество ячеек, например, так:
Теперь предположим, что вы хотите найти элемент под курсором мыши в позиции (cx, cy), В этом случае все, что нам нужно сделать, это проверить элементы в ячейке под курсором мыши:
grid_x = floor(cx / cell_size);
grid_y = floor(cy / cell_size);
for each element in cell(grid_x, grid_y):
{
if element is under cx,cy:
do something with element (hover highlight it, e.g)
}
Аналогичная вещь для обнаружения столкновений. Если мы хотим увидеть, какие элементы пересекаются (сталкиваются) с данным элементом:
grid_x1 = floor(element.x1 / cell_size);
grid_y1 = floor(element.y1 / cell_size);
grid_x2 = floor(element.x2 / cell_size);
grid_y2 = floor(element.y2 / cell_size);
for grid_y = grid_y1, grid_y2:
{
for grid_x = grid_x1, grid_x2:
{
for each other_element in cell(grid_x, grid_y):
{
if element != other_element and collide(element, other_element):
{
// The two elements intersect. Do something in response
// to the collision.
}
}
}
}
И я рекомендую людям начать этот путь, разделив пространство / экран на фиксированное количество ячеек сетки, таких как 10x10, или 100x100, или даже 1000x1000. Некоторые люди могут подумать, что 1000x1000 будет взрывоопасным при использовании памяти, но вы можете заставить каждую ячейку требовать только 4 байта с 32-разрядными целыми числами, например так:
... в этот момент даже миллион ячеек занимает менее 4 мегабайт.
Обратная сторона сетки с фиксированным разрешением
Сетка с фиксированным разрешением - фантастическая структура данных для этой проблемы, если вы спросите меня (мой личный фаворит для обнаружения столкновений), но у нее есть некоторые недостатки.
Представьте, что у вас есть видеоигра "Властелин колец". Допустим, многие из ваших юнитов - это маленькие юниты на карте, такие как люди, орки и эльфы. Тем не менее, у вас также есть несколько гигантских юнитов, таких как драконы и энты.
Здесь проблема с фиксированным разрешением сетки состоит в том, что, хотя размеры ваших ячеек могут быть оптимальными для хранения таких маленьких юнитов, как люди, эльфы и орки, которые большую часть времени занимают всего одну клетку, огромные чуваки, такие как драконы и энты, могут захотеть занимают много клеток, скажем, 400 клеток (20х20). В результате мы должны вставить этих больших парней во многие ячейки и хранить много избыточных данных.
Также предположим, что вы хотите найти интересующую вас большую прямоугольную область карты. В этом случае вам может понадобиться проверить больше ячеек, чем теоретически оптимально.
Это основной недостаток сетки с фиксированным разрешением *. В конечном итоге нам может понадобиться вставить большие объекты и сохранить их в гораздо большем количестве ячеек, чем в идеале, и в больших областях поиска нам, возможно, придется проверять гораздо больше ячеек, чем в идеале для поиска.
- Тем не менее, если оставить в стороне теорию, часто вы можете работать с сетками способом, который очень удобен для кэширования способами, подобными обработке изображений. В результате, хотя у него есть эти теоретические недостатки, на практике простота и легкость реализации удобных для кэша шаблонов обхода может сделать сетку намного лучше, чем кажется.
Quadtrees
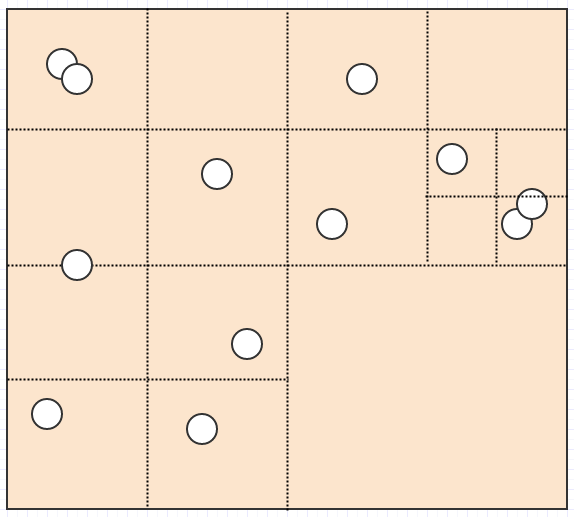
Таким образом, дерево является одним из решений этой проблемы. Вместо того чтобы использовать, так сказать, сетку с фиксированным разрешением, они адаптируют разрешение на основе некоторых критериев, подразделяя / разбивая на 4 дочерние ячейки для увеличения разрешения. Например, мы можем сказать, что ячейка должна делиться, если в данной ячейке более 2 детей. В этом случае это:
Заканчивается тем, что становится таким:
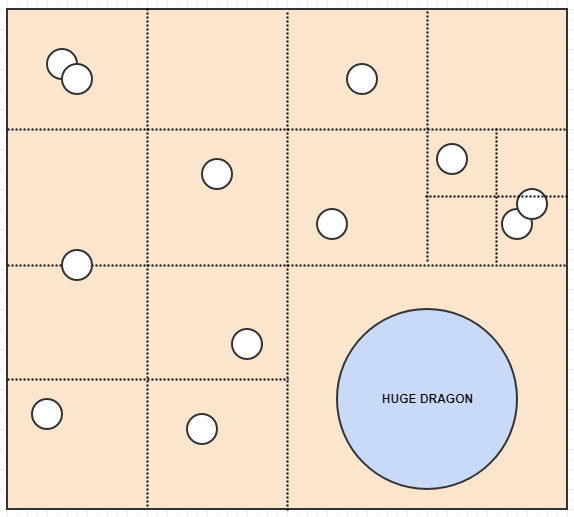
И теперь у нас есть довольно хорошее представление, где ни одна ячейка не хранит более 2 элементов. А пока давайте рассмотрим, что произойдет, если мы вставим огромного дракона:
Здесь, в отличие от сетки с фиксированным разрешением, дракона можно просто вставить в одну ячейку, поскольку ячейка, в которой он находится, содержит только один элемент. Аналогично, если мы будем искать большую область карты, нам не нужно будет проверять так много ячеек, если в них не будет много элементов.
Реализация
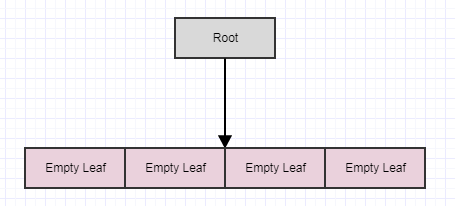
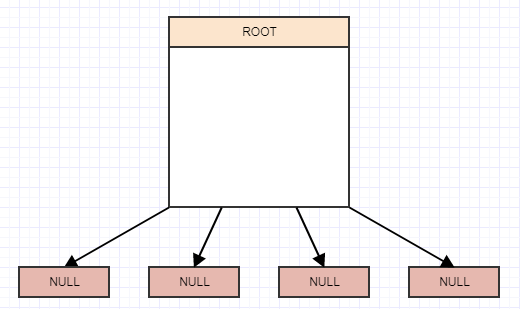
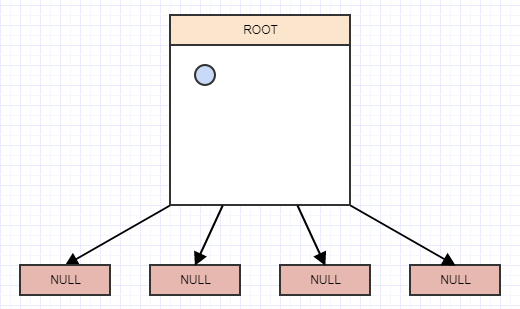
Так как же нам реализовать одну из этих штук? Ну, в конце дня это дерево, а в этом - 4 дерева. Итак, мы начнем с понятия корневого узла с четырьмя дочерними элементами, но в настоящее время они имеют значение null/nil, и в настоящий момент корень также является листом:
вставка
Давайте начнем вставлять некоторые элементы, и снова для простоты, скажем, узел должен разделиться, когда он имеет более 2 элементов. Таким образом, мы вставим элемент, и когда мы вставим элемент, мы должны вставить его в листья (ячейки), к которым он принадлежит. В этом случае у нас есть только один, корневой узел / ячейка, и мы вставим его туда:
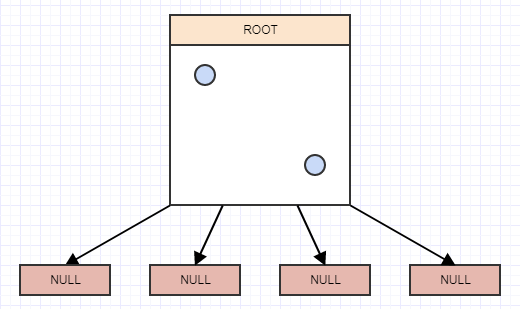
... и давайте вставим другое:
... и еще одно:
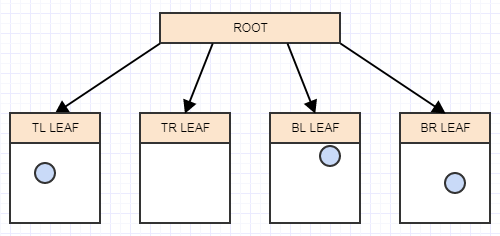
И теперь у нас более 2 элементов в листовом узле. Теперь он должен расколоться. На этом этапе мы создаем 4 дочерних элемента для конечного узла (в данном случае нашего корня), а затем переносим элементы из разделяемого листа (корневого элемента) в соответствующие квадранты на основе области / ячейки, которую каждый элемент занимает в пространстве:
Давайте вставим другой элемент и снова в соответствующий лист, к которому он принадлежит:
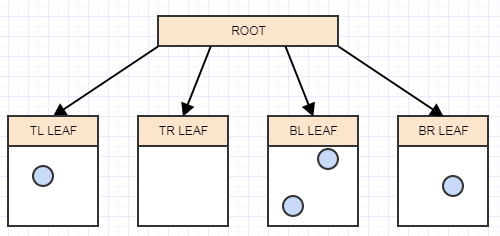
... и другой:
И теперь у нас снова более 2 элементов в листе, поэтому мы должны разделить его на 4 квадранта (дочерние):
И это основная идея. Вы можете заметить, что когда мы вставляем элементы, которые не являются бесконечно малыми точками, они могут легко перекрывать несколько ячеек / узлов.
В результате, если у нас будет много элементов, которые перекрывают много границ между ячейками, они могут в конечном итоге захотеть разделить целое, возможно, бесконечно. Чтобы смягчить эту проблему, некоторые люди решили разделить элемент. Если все, что вы связываете с элементом, это прямоугольник, довольно просто нарезать прямоугольники. Другие люди могут просто установить предел глубины / рекурсии для того, сколько дерева может разделить. Я предпочитаю последнее решение для сценариев обнаружения столкновений между этими двумя, так как я считаю, что по крайней мере проще реализовать его более эффективно. Однако есть другая альтернатива: свободные представления, и это будет рассмотрено в другом разделе.
Кроме того, если у вас есть элементы прямо друг над другом, то ваше дерево может хотеть разделяться бесконечно, даже если вы храните бесконечно малые точки. Например, если у вас есть 25 точек прямо друг над другом в пространстве (сценарий, с которым я довольно часто сталкиваюсь в VFX), то ваше дерево будет хотеть делиться бесконечно без ограничения рекурсии / глубины, несмотря ни на что. В результате, для обработки патологических случаев вам может потребоваться ограничение глубины, даже если вы нарезаете кубиками элементы.
Удаление элементов
Удаление элементов рассматривается в первом ответе вместе с удалением узлов, чтобы очистить дерево и удалить пустые листья. Но в основном все, что мы делаем, чтобы удалить элемент, используя мой предложенный подход, - это просто спуститься вниз по дереву, где находится лист / листья, в которых хранится элемент (который вы можете определить, например, по его прямоугольнику), и удалить его из этих листьев.
Затем, чтобы начать удаление пустых конечных узлов, мы используем подход отложенной очистки, описанный в исходном ответе.
Заключение
У меня мало времени, но я постараюсь вернуться к этому и продолжать улучшать ответ. Если люди хотят выполнить упражнение, я бы предложил использовать простую старую сетку с фиксированным разрешением и посмотреть, сможете ли вы получить ее там, где каждая ячейка представляет собой просто 32-разрядное целое число. Прежде чем рассматривать квадродерево, сначала разберитесь с сеткой и ее внутренними проблемами, и вы можете быть в порядке с сеткой. Это может даже предоставить вам наиболее оптимальное решение в зависимости от того, насколько эффективно вы можете реализовать сетку по сравнению с квадродеревом.
5. Свободная / плотная двойная сетка с агентами 500k
Выше приведен небольшой GIF, показывающий 500000 агентов, отскакивающих друг от друга каждый раз, используя новую структуру данных "свободная / плотная сетка", которую я вдохновил создать после написания ответа о свободных ветвях деревьев. Я постараюсь рассказать, как это работает.
На сегодняшний день это самая эффективная структура данных среди всех тех, что я продемонстрировал, которые я реализовал (хотя это может быть только я), обрабатывая полмиллиона агентов лучше, чем исходное квадродерево, обработанное 100 Кб, и лучше, чем свободный квадри дерево обработано 250к. Это также требует наименьшего количества памяти и имеет наиболее стабильное использование памяти среди этих трех. Все это по-прежнему работает в одном потоке, без SIMD-кода, без изящных микрооптимизаций, как я обычно делаю, для производственного кода - просто прямая реализация из пары часов работы.
Я также улучшил узкие места при рисовании, не улучшая мой код растеризации. Это потому, что сетка позволяет мне легко проходить ее таким образом, чтобы она была удобна для кеширования при обработке изображений (поочередное рисование элементов в ячейках сетки по совпадению приводит к очень дружественным к кешу шаблонам обработки изображений при растеризации).
Как ни странно, мне потребовалось также самое короткое время для реализации (всего 2 часа, пока я потратил 5 или 6 часов на свободное квадродерево), и это также требует наименьшего количества кода (и, возможно, имеет самый простой код). Хотя это может быть только потому, что я накопил так много опыта внедрения гридов.
Свободная / Плотная Двойная Сетка
Итак, я рассказал о том, как сетки работали в разделе основы (см. Часть 2), но это "свободная сетка". Каждая ячейка сетки хранит свою собственную ограничивающую рамку, которая может уменьшаться при удалении элементов и расти при добавлении элементов. В результате каждый элемент должен быть вставлен в сетку только один раз, в зависимости от того, в какую ячейку попадает его центральное положение, например:
// Ideally use multiplication here with inv_cell_w or inv_cell_h.
int cell_x = clamp(floor(elt_x / cell_w), 0, num_cols-1);
int cell_y = clamp(floor(ely_y / cell_h), 0, num_rows-1);
int cell_idx = cell_y*num_rows + cell_x;
// Insert element to cell at 'cell_idx' and expand the loose cell's AABB.
В ячейках хранятся элементы и AABB, например:
struct LGridLooseCell
{
// Stores the index to the first element using an indexed SLL.
int head;
// Stores the extents of the grid cell relative to the upper-left corner
// of the grid which expands and shrinks with the elements inserted and
// removed.
float l, t, r, b;
};
Тем не менее, свободные клетки представляют концептуальную проблему. Учитывая, что у них есть эти ограничивающие рамки, которые могут стать огромными, если мы вставим огромный элемент, как мы можем избежать проверки каждой отдельной ячейки сетки, если мы хотим выяснить, какие свободные ячейки и элементы внутри пересекают прямоугольник поиска, например?
И на самом деле это "двойная свободная сетка". Слабые ячейки сетки разбиты на плотную сетку. Когда мы делаем аналогичный поиск выше, мы сначала просматриваем узкую сетку следующим образом:
tx1 = clamp(floor(search_x1 / cell_w), 0, num_cols-1);
tx2 = clamp(floor(search_x2 / cell_w), 0, num_cols-1);
ty1 = clamp(floor(search_y1 / cell_h), 0, num_rows-1);
ty2 = clamp(floor(search_y2 / cell_h), 0, num_rows-1);
for ty = ty1, ty2:
{
trow = ty * num_cols
for tx = tx1, tx2:
{
tight_cell = tight_cells[trow + tx];
for each loose_cell in tight_cell:
{
if loose_cell intersects search area:
{
for each element in loose_cell:
{
if element intersects search area:
add element to query results
}
}
}
}
}
Плотные ячейки хранят односвязный индексный список свободных ячеек, например:
struct LGridLooseCellNode
{
// Points to the next loose cell node in the tight cell.
int next;
// Stores an index to the loose cell.
int cell_idx;
};
struct LGridTightCell
{
// Stores the index to the first loose cell node in the tight cell using
// an indexed SLL.
int head;
};
И вуаля, это основная идея "свободной двойной сетки". Когда мы вставляем элемент, мы расширяем AABB свободной ячейки так же, как мы делаем для свободного дерева квадрантов. Однако мы также вставляем свободную ячейку в узкую сетку на основе ее прямоугольника (и она может быть вставлена в несколько ячеек).
Комбинация этих двух элементов (плотная сетка для быстрого поиска незакрепленных ячеек и незакрепленных ячеек для быстрого поиска элементов) дает прекрасную структуру данных, в которой каждый элемент вставляется в одну ячейку с постоянным поиском, вставкой и удалением.
Единственный большой недостаток, который я вижу, заключается в том, что мы должны хранить все эти ячейки и, возможно, по-прежнему должны искать больше ячеек, чем нам нужно, но они все еще достаточно дешевы (в моем случае 20 байт на ячейку), и легко пройти ячейки при поиске в очень удобной для кэша схеме доступа.
Я рекомендую попробовать эту идею "свободных сеток". Возможно, его гораздо проще реализовать, чем квадродерево и потерять квадродерево, и, что более важно, оптимизировать, поскольку он сразу поддается макету памяти, дружественному к кешу. В качестве супер крутого бонуса, если вы можете заранее предвидеть количество агентов в вашем мире, он на 100% идеально стабилен и незамедлительно с точки зрения использования памяти, поскольку элемент всегда занимает ровно одну ячейку, а общее количество ячеек равно исправлено (так как они не делятся / не разделяются). В результате использование памяти очень стабильно. Это может быть огромным бонусом для определенного аппаратного и программного обеспечения, когда вы хотите заранее выделить всю память заранее и знать, что использование памяти никогда не превысит эту точку.
Также очень легко заставить его работать с SIMD для одновременного выполнения нескольких когерентных запросов с векторизованным кодом (в дополнение к многопоточности), поскольку обход, если мы можем даже назвать его таковым, является плоским (это просто поиск в постоянном времени в индекс ячейки, который включает в себя некоторую арифметику). В результате довольно легко применять стратегии оптимизации, аналогичные пакетам лучей, которые Intel применяет к своему ядру трассировки лучей /BVH (Embree) для одновременного тестирования нескольких когерентных лучей (в нашем случае это будут "агентские пакеты" для коллизий), за исключением случаев, когда такой причудливый / сложный код, так как "обход" сетки намного проще.
На использование памяти и эффективность
Я немного рассказал об этом в первой части, посвященной эффективным квадродеревам, но сокращение использования памяти часто является ключом к скорости в наши дни, поскольку наши процессоры работают очень быстро, когда вы вводите данные, скажем, в L1 или регистр, но доступ к DRAM относительно, так медленно. У нас так мало драгоценной быстрой памяти, даже если у нас безумное количество медленной памяти.
Я думаю, что мне повезло начать с того времени, когда мы должны были быть очень экономными с использованием памяти (хотя и не так много, как люди до меня), когда даже мегабайт DRAM считался удивительным. Некоторые вещи, которые я изучил в то время, и привычки, которые я приобрел (хотя я далеко не эксперт), по совпадению совпадают с производительностью.
Итак, один общий совет, который я бы дал по эффективности в целом, а не только по пространственным индексам, используемым для обнаружения столкновений, - это наблюдение за использованием памяти. Если он взрывной, скорее всего, решение будет не очень эффективным. Конечно, существует "серая зона", где использование немного большего объема памяти для структуры данных может существенно сократить обработку до такой степени, что это выгодно только с учетом скорости, но во много раз уменьшает объем памяти, необходимый для структур данных, особенно "горячей памяти". "к которому обращаются неоднократно, может переводиться довольно пропорционально улучшению скорости. Все наименее эффективные пространственные показатели, с которыми я столкнулся в своей карьере, были самыми взрывоопасными в использовании памяти.
Полезно посмотреть на объем данных, которые вам нужно хранить, и подсчитать, хотя бы приблизительно, сколько памяти в идеале должно потребоваться. Затем сравните это с тем, сколько вам на самом деле нужно. Если эти два мира разделены, то вы, вероятно, получите приличный импульс, сокращающий использование памяти, потому что это часто приводит к уменьшению времени загрузки кусков памяти из более медленных форм памяти в иерархии памяти.
4. Свободное дерево
Хорошо, я хотел потратить некоторое время на реализацию и объяснение свободных четырех деревьев, так как я нахожу их очень интересными и, возможно, даже наиболее сбалансированными для широкого спектра вариантов использования, включающих очень динамичные сцены.
В итоге я реализовал одну последнюю ночь и потратил некоторое время на настройку, настройку и профилирование. Вот тизер с четвертью миллиона динамических агентов, каждый раз двигающихся и отскакивающих друг от друга каждый раз:
Частота кадров начинает уменьшаться, когда я уменьшаю масштаб, чтобы посмотреть на все четверть миллиона агентов вместе со всеми ограничивающими прямоугольниками свободного квадродерева, но это в основном из-за узких мест в моих функциях рисования. Они начинают становиться горячими точками, если я уменьшаю масштаб, чтобы нарисовать все на экране сразу, и я даже не стал их оптимизировать. Вот как это работает на базовом уровне с очень немногими агентами:
Loose Quadtree
Хорошо, так что же такое свободные ветки дерева? Это в основном квадродерево, чьи узлы не полностью разделены на четыре четных квадранта. Вместо этого их AABB (ограничивающие прямоугольники) могут перекрываться и быть больше или часто даже меньше, чем вы получили бы, если бы вы идеально разбили узел по центру на 4 квадранта.
Так что в этом случае нам абсолютно необходимо хранить ограничивающие рамки с каждым узлом, и поэтому я представлял это так:
struct LooseQuadNode
{
// Stores the AABB of the node.
float rect[4];
// Stores the negative index to the first child for branches or the
// positive index to the element list for leaves.
int children;
};
На этот раз я попытался использовать плавающую точку одинарной точности, чтобы увидеть, как она хорошо работает, и она сделала очень приличную работу.
В чем смысл?
Хорошо, так какой в этом смысл? Главное, что вы можете использовать с свободным квадродеревом, - это то, что вы можете рассматривать каждый элемент, который вы вставляете в квадродерево, как одну точку для вставки и удаления. Поэтому элемент никогда не вставляется в более чем один листовой узел во всем дереве, поскольку он обрабатывается как бесконечно малая точка.
Однако, когда мы вставляем эти "точки элемента" в дерево, мы расширяем ограничивающие рамки каждого узла, в который мы вставляем, чтобы охватить границы элемента (например, прямоугольник элемента). Это позволяет нам надежно находить эти элементы при выполнении поискового запроса (например, поиск всех элементов, которые пересекают область прямоугольника или круга).
Плюсы:
- Даже самый гигантский агент должен быть вставлен только в один листовой узел и займет не больше памяти, чем самый маленький. В результате он хорошо подходит для сцен с элементами, размеры которых сильно варьируются от одного к другому, и это то, чем я занимался стресс-тестирование в демонстрационной программе с агентом 250k выше.
- Использует меньше памяти на элемент, особенно огромные элементы.
Минусы:
- Хотя это ускоряет вставку и удаление, оно неизбежно замедляет поиск в дереве. Раньше было несколько базовых сравнений с центральной точкой узла, чтобы определить, какие квадранты спуститься в очередь превращаются в цикл, проверяющий каждый прямоугольник каждого дочернего элемента, чтобы определить, какие из них пересекают область поиска.
- Использует больше памяти на узел (в 5 раз больше в моем случае).
Дорогие Запросы
Этот первый аргумент будет довольно ужасным для статических элементов, так как все, что мы делаем, это строим дерево и ищем его в этих случаях. И я обнаружил, что с этим свободным quadtree, несмотря на то, что он потратил несколько часов на его настройку и настройку, существует огромная горячая точка, связанная с его запросами:
Тем не менее, это на самом деле моя "лучшая" личная реализация квадродерева на данный момент для динамических сцен (хотя имейте в виду, что для этой цели я предпочитаю иерархические сетки и у меня нет особого опыта использования квадродерев для динамических сцен), несмотря на этот вопиющий довод И это потому, что, по крайней мере, для динамических сцен мы должны постоянно перемещать элементы каждый шаг по времени, и поэтому с деревом гораздо больше общего, чем просто запросить его. Он должен постоянно обновляться, и это на самом деле делает довольно приличную работу.
Что мне нравится в свободном квадри-дереве, так это то, что вы можете чувствовать себя в безопасности, даже если у вас есть лодка с массивными элементами в дополнение к лодке с самыми молодыми элементами. Массивные элементы не будут занимать больше памяти, чем маленькие. В результате, если бы я писал видеоигру с огромным миром и хотел просто бросить все в один центральный пространственный индекс, чтобы ускорить все, не беспокоясь об иерархии структур данных, как я обычно это делаю, тогда свободные ветки дерева и свободные октреи могут быть совершенно сбалансировано как "одна центральная универсальная структура данных, если мы собираемся использовать только одну для всего динамического мира".
Использование памяти
С точки зрения использования памяти, в то время как элементы занимают меньше памяти (особенно массивных), узлы занимают немного больше по сравнению с моими реализациями, где узлам даже не нужно хранить AABB. В целом, во множестве тестов, в том числе со множеством гигантских элементов, я обнаружил, что свободное квадри дерево имеет тенденцию занимать немного больше памяти из-за своих узких узлов (примерно на 33% больше, по приблизительной оценке). Тем не менее, в моем первоначальном ответе он работает лучше, чем реализация quadtree.
С другой стороны, использование памяти более стабильно (что приводит к более стабильной и плавной частоте кадров). Четырехдневное дерево моего исходного ответа заняло около 5 с, прежде чем использование памяти стало совершенно стабильным. Этот имеет тенденцию становиться стабильным только через секунду или две после запуска, и, скорее всего, потому, что элементы никогда не нужно вставлять более одного раза (даже небольшие элементы могут быть вставлены дважды в мое исходное дерево квадрантов, если они перекрывают два или более узлов на границах). В результате структура данных быстро обнаруживает необходимый объем памяти, выделяемый на все случаи, так сказать.
теория
Итак, давайте рассмотрим основную теорию. Я рекомендую начать с реализации обычного quadtree и понять его, прежде чем переходить на свободные версии, так как их немного сложнее реализовать. Когда мы начинаем с пустого дерева, вы можете представить, что оно также имеет пустой прямоугольник.
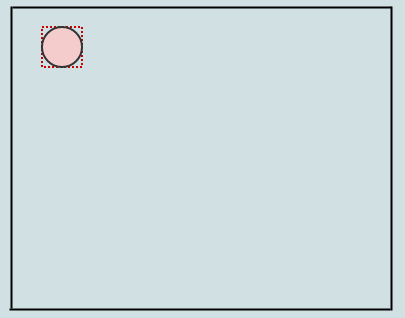
Давайте вставим один элемент:
Поскольку в данный момент у нас есть только корневой узел, который также является листом, мы просто вставляем его в него. После этого ранее пустой прямоугольник корневого узла теперь включает в себя элемент, который мы вставили (показано красными пунктирными линиями). Давайте вставим другое:
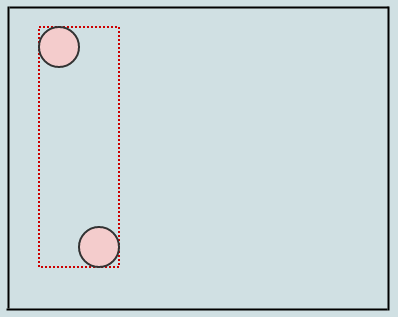
Мы расширяем AABB узлов, которые мы пересекаем, когда мы вставляем (на этот раз только корень) AABB элементов, которые мы вставляем. Давайте вставим еще один, и, скажем, узлы должны разделиться, если они содержат более 2 элементов:
В этом случае у нас есть более 2 элементов в листовом узле (нашем корне), поэтому мы должны разделить его на 4 квадранта. Это почти то же самое, что и разбиение обычного дерева точек на основе точек, за исключением того, что мы снова расширяем ограничивающие рамки при передаче дочерних элементов. Мы начнем с рассмотрения центральной позиции разделяемого узла:
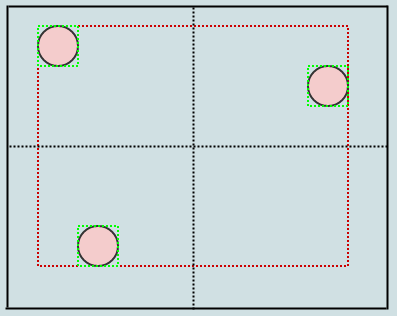
Теперь у нас есть 4 дочерних элемента к нашему корневому узлу, и каждый из них также хранит свою тесно прилегающую ограничивающую рамку (показана зеленым цветом). Давайте вставим еще один элемент:
Здесь вы можете видеть, что вставка этого элемента не только расширяет прямоугольник нижнего левого дочернего элемента, но также и корень (мы расширяем все AABB вдоль пути, который мы вставляем). Давайте вставим другое:
В этом случае у нас снова есть 3 элемента в листовом узле, поэтому мы должны разделить:
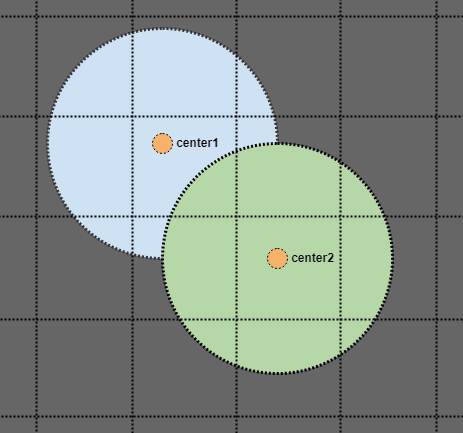
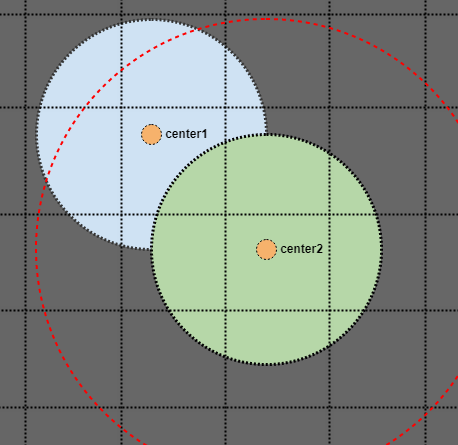
Просто так А как насчет этого круга в левом нижнем углу? Кажется, он пересекает 2 квадранта. Однако мы рассматриваем только одну точку элемента (например, его центр), чтобы определить сектор, к которому он принадлежит. Так что этот круг фактически вставляется только в нижний левый квадрант.
Однако ограничивающий прямоугольник нижнего левого квадранта расширяется, чтобы охватить его экстенты (показаны синим цветом, и надеюсь, что вы, ребята, не возражаете, но я изменил цвет BG, так как стало трудно видеть цвета), и поэтому AABBs узлы на уровне 2 (показаны синим цветом) фактически разливаются в квадранты друг друга.
Тот факт, что каждый квадрант хранит свой собственный прямоугольник, который всегда гарантированно охватывает его элементы, позволяет нам вставлять элемент только в один конечный узел, даже если его область пересекается с несколькими узлами. Вместо этого мы расширяем ограничивающий прямоугольник конечного узла вместо вставки элемента в несколько узлов.
Обновление AABB
Таким образом, это может привести к вопросу, когда обновляются AABB? Если мы будем расширять AABB только после вставки элементов, они будут иметь тенденцию расти все больше и больше. Как мы сжимаем их, когда элементы удаляются? Есть много способов справиться с этим, но я делаю это, обновляя ограничивающие рамки всей иерархии в том методе "очистки", который описан в моем первоначальном ответе. Это кажется достаточно быстрым (даже не отображается как горячая точка).
По сравнению с сетками
Я до сих пор не могу реализовать это почти так же эффективно для обнаружения коллизий, как мои реализации иерархической сетки, но опять же, это может быть больше обо мне, чем структура данных. Основная сложность, с которой я сталкиваюсь в древовидных структурах, заключается в том, чтобы легко контролировать, где все находится в памяти и как к ней осуществляется доступ. С помощью сетки вы можете убедиться, что все столбцы строки являются смежными и расположены последовательно, например, и обеспечить последовательный доступ к ним вместе с элементами, непрерывно хранящимися в этой строке. С деревом доступ к памяти имеет тенденцию быть немного спорадическим по своей природе, а также имеет тенденцию к быстрому ухудшению, поскольку деревья хотят передавать элементы намного чаще, поскольку узлы делятся на несколько дочерних элементов. Тем не менее, если я хочу использовать пространственный индекс, который был деревом, я действительно пока копаю эти свободные варианты, и в моей голове появляются идеи для реализации "свободной сетки".
Заключение
Таким образом, в двух словах это свободные ветки дерева, и у него в основном есть логика вставки / удаления обычного дерева дерева, которое просто хранит точки, за исключением того, что оно расширяет / обновляет AABB в пути. Для поиска мы в конечном итоге пересекаем все дочерние узлы, прямоугольники которых пересекают нашу область поиска.
Я надеюсь, что люди не возражают против того, чтобы я отправлял так много длинных ответов. Я действительно получаю удовольствие от их написания, и для меня было полезным упражнение при повторном посещении ветвей деревьев, чтобы попытаться написать все эти ответы. Я также обдумываю книгу на эти темы в какой-то момент (хотя она будет на японском языке) и пишу здесь некоторые ответы, хотя и поспешно и на английском, помогает мне как-то собрать все вместе в моем мозгу. Теперь мне просто нужно, чтобы кто-то попросил объяснить, как написать эффективные октреи или сетки с целью обнаружения столкновений, чтобы дать мне повод сделать то же самое по этим предметам.
3. Портативная реализация C
Я надеюсь, что люди не возражают против другого ответа, но я исчерпал предел 30 КБ. Сегодня я думал о том, что мой первый ответ не был очень независимым от языка. Я говорил о стратегиях распределения памяти, шаблонах классов и т. Д., И не все языки допускают такие вещи.
Поэтому я потратил некоторое время на размышления об эффективной реализации, которая почти повсеместно применима (исключение составляют функциональные языки). Так что я закончил тем, что портировал свое квадродерево на C таким образом, что все, что ему нужно, это массивы int хранить все.
Результат не очень приятный, но должен работать очень эффективно на любом языке, который позволяет хранить непрерывные массивы int, Для Python есть библиотеки вроде ndarray в numpy, Для JS есть типизированные массивы. Для Java и C# мы можем использовать int массивы (не Integerне гарантируется, что они будут храниться смежно, и они используют намного больше памяти, чем старые int).
C IntList
Поэтому я использую одну вспомогательную структуру, построенную на int массивы для всего дерева quadtree, чтобы сделать его максимально простым для переноса на другие языки. Он сочетает в себе стек / свободный список. Это все, что нам нужно, чтобы эффективно реализовать все, о чем говорилось в другом ответе.
#ifndef INT_LIST_H
#define INT_LIST_H
#ifdef __cplusplus
#define IL_FUNC extern "C"
#else
#define IL_FUNC
#endif
typedef struct IntList IntList;
enum {il_fixed_cap = 128};
struct IntList
{
// Stores a fixed-size buffer in advance to avoid requiring
// a heap allocation until we run out of space.
int fixed[il_fixed_cap];
// Points to the buffer used by the list. Initially this will
// point to 'fixed'.
int* data;
// Stores how many integer fields each element has.
int num_fields;
// Stores the number of elements in the list.
int num;
// Stores the capacity of the array.
int cap;
// Stores an index to the free element or -1 if the free list
// is empty.
int free_element;
};
// ---------------------------------------------------------------------------------
// List Interface
// ---------------------------------------------------------------------------------
// Creates a new list of elements which each consist of integer fields.
// 'num_fields' specifies the number of integer fields each element has.
IL_FUNC void il_create(IntList* il, int num_fields);
// Destroys the specified list.
IL_FUNC void il_destroy(IntList* il);
// Returns the number of elements in the list.
IL_FUNC int il_size(const IntList* il);
// Returns the value of the specified field for the nth element.
IL_FUNC int il_get(const IntList* il, int n, int field);
// Sets the value of the specified field for the nth element.
IL_FUNC void il_set(IntList* il, int n, int field, int val);
// Clears the specified list, making it empty.
IL_FUNC void il_clear(IntList* il);
// ---------------------------------------------------------------------------------
// Stack Interface (do not mix with free list usage; use one or the other)
// ---------------------------------------------------------------------------------
// Inserts an element to the back of the list and returns an index to it.
IL_FUNC int il_push_back(IntList* il);
// Removes the element at the back of the list.
IL_FUNC void il_pop_back(IntList* il);
// ---------------------------------------------------------------------------------
// Free List Interface (do not mix with stack usage; use one or the other)
// ---------------------------------------------------------------------------------
// Inserts an element to a vacant position in the list and returns an index to it.
IL_FUNC int il_insert(IntList* il);
// Removes the nth element in the list.
IL_FUNC void il_erase(IntList* il, int n);
#endif
#include "IntList.h"
#include <stdlib.h>
#include <string.h>
#include <assert.h>
void il_create(IntList* il, int num_fields)
{
il->data = il->fixed;
il->num = 0;
il->cap = il_fixed_cap;
il->num_fields = num_fields;
il->free_element = -1;
}
void il_destroy(IntList* il)
{
// Free the buffer only if it was heap allocated.
if (il->data != il->fixed)
free(il->data);
}
void il_clear(IntList* il)
{
il->num = 0;
il->free_element = -1;
}
int il_size(const IntList* il)
{
return il->num;
}
int il_get(const IntList* il, int n, int field)
{
assert(n >= 0 && n < il->num);
return il->data[n*il->num_fields + field];
}
void il_set(IntList* il, int n, int field, int val)
{
assert(n >= 0 && n < il->num);
il->data[n*il->num_fields + field] = val;
}
int il_push_back(IntList* il)
{
const int new_pos = (il->num+1) * il->num_fields;
// If the list is full, we need to reallocate the buffer to make room
// for the new element.
if (new_pos > il->cap)
{
// Use double the size for the new capacity.
const int new_cap = new_pos * 2;
// If we're pointing to the fixed buffer, allocate a new array on the
// heap and copy the fixed buffer contents to it.
if (il->cap == il_fixed_cap)
{
il->data = malloc(new_cap * sizeof(*il->data));
memcpy(il->data, il->fixed, sizeof(il->fixed));
}
else
{
// Otherwise reallocate the heap buffer to the new size.
il->data = realloc(il->data, new_cap * sizeof(*il->data));
}
// Set the old capacity to the new capacity.
il->cap = new_cap;
}
return il->num++;
}
void il_pop_back(IntList* il)
{
// Just decrement the list size.
assert(il->num > 0);
--il->num;
}
int il_insert(IntList* il)
{
// If there's a free index in the free list, pop that and use it.
if (il->free_element != -1)
{
const int index = il->free_element;
const int pos = index * il->num_fields;
// Set the free index to the next free index.
il->free_element = il->data[pos];
// Return the free index.
return index;
}
// Otherwise insert to the back of the array.
return il_push_back(il);
}
void il_erase(IntList* il, int n)
{
// Push the element to the free list.
const int pos = n * il->num_fields;
il->data[pos] = il->free_element;
il->free_element = n;
}
Использование IntList
Использование этой структуры данных для реализации всего не дает самого красивого кода. Вместо доступа к элементам и полям, как это:
elements[n].field = elements[n].field + 1;
... в итоге мы делаем это так:
il_set(&elements, n, idx_field, il_get(&elements, n, idx_field) + 1);
... это отвратительно, я знаю, но смысл этого кода в том, чтобы быть максимально эффективным и переносимым, а не настолько простым в обслуживании, насколько это возможно. Надежда состоит в том, что люди могут просто использовать это квадродерево для своих проектов, не изменяя его и не поддерживая его.
Ох, и не стесняйтесь использовать этот код, который я публикую, как вы хотите, даже для коммерческих проектов. Мне бы очень понравилось, если бы люди сообщили мне, если они находят это полезным, но делайте так, как вы хотите.
C Quadtree
Итак, используя приведенную выше структуру данных, вот дерево в C:
#ifndef QUADTREE_H
#define QUADTREE_H
#include "IntList.h"
#ifdef __cplusplus
#define QTREE_FUNC extern "C"
#else
#define QTREE_FUNC
#endif
typedef struct Quadtree Quadtree;
struct Quadtree
{
// Stores all the nodes in the quadtree. The first node in this
// sequence is always the root.
IntList nodes;
// Stores all the elements in the quadtree.
IntList elts;
// Stores all the element nodes in the quadtree.
IntList enodes;
// Stores the quadtree extents.
int root_mx, root_my, root_sx, root_sy;
// Maximum allowed elements in a leaf before the leaf is subdivided/split unless
// the leaf is at the maximum allowed tree depth.
int max_elements;
// Stores the maximum depth allowed for the quadtree.
int max_depth;
// Temporary buffer used for queries.
char* temp;
// Stores the size of the temporary buffer.
int temp_size;
};
// Function signature used for traversing a tree node.
typedef void QtNodeFunc(Quadtree* qt, void* user_data, int node, int depth, int mx, int my, int sx, int sy);
// Creates a quadtree with the requested extents, maximum elements per leaf, and maximum tree depth.
QTREE_FUNC void qt_create(Quadtree* qt, int width, int height, int max_elements, int max_depth);
// Destroys the quadtree.
QTREE_FUNC void qt_destroy(Quadtree* qt);
// Inserts a new element to the tree.
// Returns an index to the new element.
QTREE_FUNC int qt_insert(Quadtree* qt, int id, float x1, float y1, float x2, float y2);
// Removes the specified element from the tree.
QTREE_FUNC void qt_remove(Quadtree* qt, int element);
// Cleans up the tree, removing empty leaves.
QTREE_FUNC void qt_cleanup(Quadtree* qt);
// Outputs a list of elements found in the specified rectangle.
QTREE_FUNC void qt_query(Quadtree* qt, IntList* out, float x1, float y1, float x2, float y2, int omit_element);
// Traverses all the nodes in the tree, calling 'branch' for branch nodes and 'leaf'
// for leaf nodes.
QTREE_FUNC void qt_traverse(Quadtree* qt, void* user_data, QtNodeFunc* branch, QtNodeFunc* leaf);
#endif
#include "Quadtree.h"
#include <stdlib.h>
enum
{
// ----------------------------------------------------------------------------------------
// Element node fields:
// ----------------------------------------------------------------------------------------
enode_num = 2,
// Points to the next element in the leaf node. A value of -1
// indicates the end of the list.
enode_idx_next = 0,
// Stores the element index.
enode_idx_elt = 1,
// ----------------------------------------------------------------------------------------
// Element fields:
// ----------------------------------------------------------------------------------------
elt_num = 5,
// Stores the rectangle encompassing the element.
elt_idx_lft = 0, elt_idx_top = 1, elt_idx_rgt = 2, elt_idx_btm = 3,
// Stores the ID of the element.
elt_idx_id = 4,
// ----------------------------------------------------------------------------------------
// Node fields:
// ----------------------------------------------------------------------------------------
node_num = 2,
// Points to the first child if this node is a branch or the first element
// if this node is a leaf.
node_idx_fc = 0,
// Stores the number of elements in the node or -1 if it is not a leaf.
node_idx_num = 1,
// ----------------------------------------------------------------------------------------
// Node data fields:
// ----------------------------------------------------------------------------------------
nd_num = 6,
// Stores the extents of the node using a centered rectangle and half-size.
nd_idx_mx = 0, nd_idx_my = 1, nd_idx_sx = 2, nd_idx_sy = 3,
// Stores the index of the node.
nd_idx_index = 4,
// Stores the depth of the node.
nd_idx_depth = 5,
};
static void node_insert(Quadtree* qt, int index, int depth, int mx, int my, int sx, int sy, int element);
static int floor_int(float val)
{
return (int)val;
}
static int intersect(int l1, int t1, int r1, int b1,
int l2, int t2, int r2, int b2)
{
return l2 <= r1 && r2 >= l1 && t2 <= b1 && b2 >= t1;
}
void leaf_insert(Quadtree* qt, int node, int depth, int mx, int my, int sx, int sy, int element)
{
// Insert the element node to the leaf.
const int nd_fc = il_get(&qt->nodes, node, node_idx_fc);
il_set(&qt->nodes, node, node_idx_fc, il_insert(&qt->enodes));
il_set(&qt->enodes, il_get(&qt->nodes, node, node_idx_fc), enode_idx_next, nd_fc);
il_set(&qt->enodes, il_get(&qt->nodes, node, node_idx_fc), enode_idx_elt, element);
// If the leaf is full, split it.
if (il_get(&qt->nodes, node, node_idx_num) == qt->max_elements && depth < qt->max_depth)
{
int fc = 0, j = 0;
IntList elts = {0};
il_create(&elts, 1);
// Transfer elements from the leaf node to a list of elements.
while (il_get(&qt->nodes, node, node_idx_fc) != -1)
{
const int index = il_get(&qt->nodes, node, node_idx_fc);
const int next_index = il_get(&qt->enodes, index, enode_idx_next);
const int elt = il_get(&qt->enodes, index, enode_idx_elt);
// Pop off the element node from the leaf and remove it from the qt.
il_set(&qt->nodes, node, node_idx_fc, next_index);
il_erase(&qt->enodes, index);
// Insert element to the list.
il_set(&elts, il_push_back(&elts), 0, elt);
}
// Start by allocating 4 child nodes.
fc = il_insert(&qt->nodes);
il_insert(&qt->nodes);
il_insert(&qt->nodes);
il_insert(&qt->nodes);
il_set(&qt->nodes, node, node_idx_fc, fc);
// Initialize the new child nodes.
for (j=0; j < 4; ++j)
{
il_set(&qt->nodes, fc+j, node_idx_fc, -1);
il_set(&qt->nodes, fc+j, node_idx_num, 0);
}
// Transfer the elements in the former leaf node to its new children.
il_set(&qt->nodes, node, node_idx_num, -1);
for (j=0; j < il_size(&elts); ++j)
node_insert(qt, node, depth, mx, my, sx, sy, il_get(&elts, j, 0));
il_destroy(&elts);
}
else
{
// Increment the leaf element count.
il_set(&qt->nodes, node, node_idx_num, il_get(&qt->nodes, node, node_idx_num) + 1);
}
}
static void push_node(IntList* nodes, int nd_index, int nd_depth, int nd_mx, int nd_my, int nd_sx, int nd_sy)
{
const int back_idx = il_push_back(nodes);
il_set(nodes, back_idx, nd_idx_mx, nd_mx);
il_set(nodes, back_idx, nd_idx_my, nd_my);
il_set(nodes, back_idx, nd_idx_sx, nd_sx);
il_set(nodes, back_idx, nd_idx_sy, nd_sy);
il_set(nodes, back_idx, nd_idx_index, nd_index);
il_set(nodes, back_idx, nd_idx_depth, nd_depth);
}
static void find_leaves(IntList* out, const Quadtree* qt, int node, int depth,
int mx, int my, int sx, int sy,
int lft, int top, int rgt, int btm)
{
IntList to_process = {0};
il_create(&to_process, nd_num);
push_node(&to_process, node, depth, mx, my, sx, sy);
while (il_size(&to_process) > 0)
{
const int back_idx = il_size(&to_process) - 1;
const int nd_mx = il_get(&to_process, back_idx, nd_idx_mx);
const int nd_my = il_get(&to_process, back_idx, nd_idx_my);
const int nd_sx = il_get(&to_process, back_idx, nd_idx_sx);
const int nd_sy = il_get(&to_process, back_idx, nd_idx_sy);
const int nd_index = il_get(&to_process, back_idx, nd_idx_index);
const int nd_depth = il_get(&to_process, back_idx, nd_idx_depth);
il_pop_back(&to_process);
// If this node is a leaf, insert it to the list.
if (il_get(&qt->nodes, nd_index, node_idx_num) != -1)
push_node(out, nd_index, nd_depth, nd_mx, nd_my, nd_sx, nd_sy);
else
{
// Otherwise push the children that intersect the rectangle.
const int fc = il_get(&qt->nodes, nd_index, node_idx_fc);
const int hx = nd_sx >> 1, hy = nd_sy >> 1;
const int l = nd_mx-hx, t = nd_my-hx, r = nd_mx+hx, b = nd_my+hy;
if (top <= nd_my)
{
if (lft <= nd_mx)
push_node(&to_process, fc+0, nd_depth+1, l,t,hx,hy);
if (rgt > nd_mx)
push_node(&to_process, fc+1, nd_depth+1, r,t,hx,hy);
}
if (btm > nd_my)
{
if (lft <= nd_mx)
push_node(&to_process, fc+2, nd_depth+1, l,b,hx,hy);
if (rgt > nd_mx)
push_node(&to_process, fc+3, nd_depth+1, r,b,hx,hy);
}
}
}
il_destroy(&to_process);
}
static void node_insert(Quadtree* qt, int index, int depth, int mx, int my, int sx, int sy, int element)
{
// Find the leaves and insert the element to all the leaves found.
int j = 0;
IntList leaves = {0};
const int lft = il_get(&qt->elts, element, elt_idx_lft);
const int top = il_get(&qt->elts, element, elt_idx_top);
const int rgt = il_get(&qt->elts, element, elt_idx_rgt);
const int btm = il_get(&qt->elts, element, elt_idx_btm);
il_create(&leaves, nd_num);
find_leaves(&leaves, qt, index, depth, mx, my, sx, sy, lft, top, rgt, btm);
for (j=0; j < il_size(&leaves); ++j)
{
const int nd_mx = il_get(&leaves, j, nd_idx_mx);
const int nd_my = il_get(&leaves, j, nd_idx_my);
const int nd_sx = il_get(&leaves, j, nd_idx_sx);
const int nd_sy = il_get(&leaves, j, nd_idx_sy);
const int nd_index = il_get(&leaves, j, nd_idx_index);
const int nd_depth = il_get(&leaves, j, nd_idx_depth);
leaf_insert(qt, nd_index, nd_depth, nd_mx, nd_my, nd_sx, nd_sy, element);
}
il_destroy(&leaves);
}
void qt_create(Quadtree* qt, int width, int height, int max_elements, int max_depth)
{
qt->max_elements = max_elements;
qt->max_depth = max_depth;
qt->temp = 0;
qt->temp_size = 0;
il_create(&qt->nodes, node_num);
il_create(&qt->elts, elt_num);
il_create(&qt->enodes, enode_num);
// Insert the root node to the qt.
il_insert(&qt->nodes);
il_set(&qt->nodes, 0, node_idx_fc, -1);
il_set(&qt->nodes, 0, node_idx_num, 0);
// Set the extents of the root node.
qt->root_mx = width >> 1;
qt->root_my = height >> 1;
qt->root_sx = qt->root_mx;
qt->root_sy = qt->root_my;
}
void qt_destroy(Quadtree* qt)
{
il_destroy(&qt->nodes);
il_destroy(&qt->elts);
il_destroy(&qt->enodes);
free(qt->temp);
}
int qt_insert(Quadtree* qt, int id, float x1, float y1, float x2, float y2)
{
// Insert a new element.
const int new_element = il_insert(&qt->elts);
// Set the fields of the new element.
il_set(&qt->elts, new_element, elt_idx_lft, floor_int(x1));
il_set(&qt->elts, new_element, elt_idx_top, floor_int(y1));
il_set(&qt->elts, new_element, elt_idx_rgt, floor_int(x2));
il_set(&qt->elts, new_element, elt_idx_btm, floor_int(y2));
il_set(&qt->elts, new_element, elt_idx_id, id);
// Insert the element to the appropriate leaf node(s).
node_insert(qt, 0, 0, qt->root_mx, qt->root_my, qt->root_sx, qt->root_sy, new_element);
return new_element;
}
void qt_remove(Quadtree* qt, int element)
{
// Find the leaves.
int j = 0;
IntList leaves = {0};
const int lft = il_get(&qt->elts, element, elt_idx_lft);
const int top = il_get(&qt->elts, element, elt_idx_top);
const int rgt = il_get(&qt->elts, element, elt_idx_rgt);
const int btm = il_get(&qt->elts, element, elt_idx_btm);
il_create(&leaves, nd_num);
find_leaves(&leaves, qt, 0, 0, qt->root_mx, qt->root_my, qt->root_sx, qt->root_sy, lft, top, rgt, btm);
// For each leaf node, remove the element node.
for (j=0; j < il_size(&leaves); ++j)
{
const int nd_index = il_get(&leaves, j, nd_idx_index);
// Walk the list until we find the element node.
int node_index = il_get(&qt->nodes, nd_index, node_idx_fc);
int prev_index = -1;
while (node_index != -1 && il_get(&qt->enodes, node_index, enode_idx_elt) != element)
{
prev_index = node_index;
node_index = il_get(&qt->enodes, node_index, enode_idx_next);
}
if (node_index != -1)
{
// Remove the element node.
const int next_index = il_get(&qt->enodes, node_index, enode_idx_next);
if (prev_index == -1)
il_set(&qt->nodes, nd_index, node_idx_fc, next_index);
else
il_set(&qt->enodes, prev_index, enode_idx_next, next_index);
il_erase(&qt->enodes, node_index);
// Decrement the leaf element count.
il_set(&qt->nodes, nd_index, node_idx_num, il_get(&qt->nodes, nd_index, node_idx_num)-1);
}
}
il_destroy(&leaves);
// Remove the element.
il_erase(&qt->elts, element);
}
void qt_query(Quadtree* qt, IntList* out, float x1, float y1, float x2, float y2, int omit_element)
{
// Find the leaves that intersect the specified query rectangle.
int j = 0;
IntList leaves = {0};
const int elt_cap = il_size(&qt->elts);
const int qlft = floor_int(x1);
const int qtop = floor_int(y1);
const int qrgt = floor_int(x2);
const int qbtm = floor_int(y2);
if (qt->temp_size < elt_cap)
{
qt->temp_size = elt_cap;
qt->temp = realloc(qt->temp, qt->temp_size * sizeof(*qt->temp));
memset(qt->temp, 0, qt->temp_size * sizeof(*qt->temp));
}
// For each leaf node, look for elements that intersect.
il_create(&leaves, nd_num);
find_leaves(&leaves, qt, 0, 0, qt->root_mx, qt->root_my, qt->root_sx, qt->root_sy, qlft, qtop, qrgt, qbtm);
il_clear(out);
for (j=0; j < il_size(&leaves); ++j)
{
const int nd_index = il_get(&leaves, j, nd_idx_index);
// Walk the list and add elements that intersect.
int elt_node_index = il_get(&qt->nodes, nd_index, node_idx_fc);
while (elt_node_index != -1)
{
const int element = il_get(&qt->enodes, elt_node_index, enode_idx_elt);
const int lft = il_get(&qt->elts, element, elt_idx_lft);
const int top = il_get(&qt->elts, element, elt_idx_top);
const int rgt = il_get(&qt->elts, element, elt_idx_rgt);
const int btm = il_get(&qt->elts, element, elt_idx_btm);
if (!qt->temp[element] && element != omit_element && intersect(qlft,qtop,qrgt,qbtm, lft,top,rgt,btm))
{
il_set(out, il_push_back(out), 0, element);
qt->temp[element] = 1;
}
elt_node_index = il_get(&qt->enodes, elt_node_index, enode_idx_next);
}
}
il_destroy(&leaves);
// Unmark the elements that were inserted.
for (j=0; j < il_size(out); ++j)
qt->temp[il_get(out, j, 0)] = 0;
}
void qt_cleanup(Quadtree* qt)
{
IntList to_process = {0};
il_create(&to_process, 1);
// Only process the root if it's not a leaf.
if (il_get(&qt->nodes, 0, node_idx_num) == -1)
{
// Push the root index to the stack.
il_set(&to_process, il_push_back(&to_process), 0, 0);
}
while (il_size(&to_process) > 0)
{
// Pop a node from the stack.
const int node = il_get(&to_process, il_size(&to_process)-1, 0);
const int fc = il_get(&qt->nodes, node, node_idx_fc);
int num_empty_leaves = 0;
int j = 0;
il_pop_back(&to_process);
// Loop through the children.
for (j=0; j < 4; ++j)
{
const int child = fc + j;
// Increment empty leaf count if the child is an empty
// leaf. Otherwise if the child is a branch, add it to
// the stack to be processed in the next iteration.
if (il_get(&qt->nodes, child, node_idx_num) == 0)
++num_empty_leaves;
else if (il_get(&qt->nodes, child, node_idx_num) == -1)
{
// Push the child index to the stack.
il_set(&to_process, il_push_back(&to_process), 0, child);
}
}
// If all the children were empty leaves, remove them and
// make this node the new empty leaf.
if (num_empty_leaves == 4)
{
// Remove all 4 children in reverse order so that they
// can be reclaimed on subsequent insertions in proper
// order.
il_erase(&qt->nodes, fc + 3);
il_erase(&qt->nodes, fc + 2);
il_erase(&qt->nodes, fc + 1);
il_erase(&qt->nodes, fc + 0);
// Make this node the new empty leaf.
il_set(&qt->nodes, node, node_idx_fc, -1);
il_set(&qt->nodes, node, node_idx_num, 0);
}
}
il_destroy(&to_process);
}
void qt_traverse(Quadtree* qt, void* user_data, QtNodeFunc* branch, QtNodeFunc* leaf)
{
IntList to_process = {0};
il_create(&to_process, nd_num);
push_node(&to_process, 0, 0, qt->root_mx, qt->root_my, qt->root_sx, qt->root_sy);
while (il_size(&to_process) > 0)
{
const int back_idx = il_size(&to_process) - 1;
const int nd_mx = il_get(&to_process, back_idx, nd_idx_mx);
const int nd_my = il_get(&to_process, back_idx, nd_idx_my);
const int nd_sx = il_get(&to_process, back_idx, nd_idx_sx);
const int nd_sy = il_get(&to_process, back_idx, nd_idx_sy);
const int nd_index = il_get(&to_process, back_idx, nd_idx_index);
const int nd_depth = il_get(&to_process, back_idx, nd_idx_depth);
const int fc = il_get(&qt->nodes, nd_index, node_idx_fc);
il_pop_back(&to_process);
if (il_get(&qt->nodes, nd_index, node_idx_num) == -1)
{
// Push the children of the branch to the stack.
const int hx = nd_sx >> 1, hy = nd_sy >> 1;
const int l = nd_mx-hx, t = nd_my-hx, r = nd_mx+hx, b = nd_my+hy;
push_node(&to_process, fc+0, nd_depth+1, l,t, hx,hy);
push_node(&to_process, fc+1, nd_depth+1, r,t, hx,hy);
push_node(&to_process, fc+2, nd_depth+1, l,b, hx,hy);
push_node(&to_process, fc+3, nd_depth+1, r,b, hx,hy);
if (branch)
branch(qt, user_data, nd_index, nd_depth, nd_mx, nd_my, nd_sx, nd_sy);
}
else if (leaf)
leaf(qt, user_data, nd_index, nd_depth, nd_mx, nd_my, nd_sx, nd_sy);
}
il_destroy(&to_process);
}
Временное заключение
Это не очень хороший ответ, но я постараюсь вернуться и продолжить его редактирование. Однако приведенный выше код должен быть очень эффективным практически на любом языке, который допускает непрерывные массивы простых старых целых чисел. Пока у нас есть такая гарантия смежности, мы можем создать очень дружественное к кешу квадродерево, которое использует очень маленькую область памяти.
Пожалуйста, обратитесь к исходному ответу для получения подробной информации об общем подходе.
Грязный трюк: одинаковые размеры
В этом ответе я расскажу об уловке, которая может позволить вашему моделированию работать на порядок быстрее, если данные будут подходящими (что часто случается во многих видеоиграх, например). Это может дать вам от десятков тысяч до сотен тысяч агентов или от сотен тысяч агентов до миллионов агентов. До сих пор я не применял его ни в одной из демонстраций, показанных в моих ответах, поскольку это было немного обманом, но я использовал его в производстве, и это может изменить мир к лучшему. И как ни странно, я не вижу, чтобы это обсуждалось так часто. На самом деле я никогда не видел, чтобы это обсуждалось, что странно.
Итак, давайте вернемся к примеру Властелина колец. У нас много юнитов "человеческого размера", таких как люди, эльфы, гномы, орки и хоббиты, и у нас также есть несколько огромных юнитов, таких как драконы и энты.
Единицы "человеческого размера" не сильно различаются по размеру. Хоббит может быть четырех футов ростом и немного приземистым, а орк - 6'4. Есть некоторая разница, но это не эпическая разница. Это не разница на порядок.
Так что же произойдет, если мы поместим ограничивающую сферу / коробку вокруг хоббита размером с ограничивающую сферу / коробку орка только для грубых запросов на пересечение (прежде чем перейти к проверке более истинного столкновения на гранулярном / точном уровне)? Там немного впустую негативного пространства, но происходит нечто действительно интересное.
Если мы можем предвидеть такую верхнюю границу для блоков общего случая, мы можем сохранить их в структуре данных, которая предполагает, что все вещи имеют одинаковый размер верхней границы. Пара действительно интересных вещей происходит в этом случае:
- Нам не нужно хранить размер с каждым элементом. Структура данных может предполагать, что все элементы, вставленные в нее, имеют одинаковый одинаковый размер (только для грубых запросов на пересечение). Это может почти вдвое сократить использование памяти для элементов во многих сценариях и, естественно, ускоряет обход, когда у нас меньше памяти / данных для доступа к элементу.
- Мы можем хранить элементы только в одной ячейке / узле, даже для узких представлений, которые не имеют AABB переменного размера, хранящихся в ячейках / узлах.
Хранение только одной точки
Эта вторая часть хитрая, но представьте, что у нас есть такой случай:
Что ж, если мы посмотрим на зеленый круг и поищем его радиус, мы в конечном итоге упустим центральную точку синего круга, если он будет храниться только как одна точка в нашем пространственном индексе. Но что, если мы будем искать область, в два раза превышающую радиус наших кругов?
В этом случае мы нашли бы пересечение, даже если синий круг сохраняется только как одна точка в нашем пространственном индексе (центральная точка оранжевого цвета). Просто чтобы визуально показать, что это работает:
В этом случае окружности не пересекаются, и мы видим, что центральная точка находится за пределами даже расширенного удвоенного радиуса поиска. Таким образом, до тех пор, пока мы ищем двойной радиус в пространственном индексе, который предполагает, что все элементы имеют одинаковый размер верхней границы, мы гарантированно найдем их в грубом запросе, если мы будем искать область, в два раза превышающую радиус верхней границы (или в два раза больше прямоугольной половины для AABB).
Теперь это может показаться расточительным, поскольку в наших поисковых запросах будет проверяться больше ячеек / узлов, чем необходимо, но это только потому, что я нарисовал диаграмму для наглядности. Если вы используете эту стратегию, вы будете использовать ее для элементов, размеры которых, как правило, составляют часть размера одного конечного узла / ячейки.
Огромная оптимизация
Поэтому огромная оптимизация, которую вы можете применить, состоит в том, чтобы разделить ваш контент на 3 различных типа:
- Динамический набор (постоянно движущийся и анимирующий) с верхним пределом общего случая, таким как люди, орки, эльфы и хоббиты. Мы в основном помещаем ограничивающую рамку / сферу одинакового размера вокруг всех этих агентов. Здесь вы можете использовать плотное представление, такое как узкое квадродерево или узкая сетка, и оно будет хранить только одну точку для каждого элемента. Вы могли бы также использовать другой экземпляр этой же структуры для супер маленьких элементов, таких как феи и кнуты с другим общим верхним размером.
- Динамический набор, превышающий любую предсказуемую верхнюю границу общего случая, такую как драконы и энты с очень необычными размерами. Здесь вы можете использовать свободное представление, например, свободное дерево квадрантов или мою "свободную / жесткую двойную сетку".
- Статический набор, в котором вы можете позволить себе структуры, создание которых занимает больше времени или которые крайне неэффективны для обновления, например, квадродерево для статических данных, в котором все хранится совершенно непрерывно. В этом случае не имеет значения, насколько неэффективна структура данных для обновления, если она обеспечивает самые быстрые поисковые запросы, поскольку вы никогда не будете обновлять ее. Вы можете использовать это для элементов в вашем мире, таких как замки, баррикады и валуны.
Таким образом, идея разделения элементов общего случая с равномерными верхними границами (ограничивающими сферами или прямоугольниками) может быть чрезвычайно полезной стратегией оптимизации, если вы можете применить ее. Это также тот, который я не вижу обсуждаемым. Я часто вижу, как разработчики говорят о разделении динамического и статического контента, но вы можете добиться такого же улучшения, если не больше, если дополнительно группировать динамические элементы одинакового размера в общем случае и обрабатывать их так, как если бы они имели одинаковые размеры верхней границы для вашего грубые тесты столкновений, которые позволяют хранить их как бесконечно малую точку, которая вставляется только в один конечный узел в вашей узкой структуре данных.
О преимуществах "Обмана"
Так что это решение не очень умное или интересное, но я думаю, что стоит упомянуть об этом, по крайней мере, для тех, кто похож на меня. Я потратил большую часть своей карьеры в поисках "убер" решений: единый размер подходит для всех структур данных и алгоритмов, которые прекрасно справляются с любым вариантом использования, в надежде на то, что у него будет возможность потратить немного времени заранее, чтобы получить его. правильно, а затем использовать его как сумасшедший далеко в будущем и в разных случаях использования, не говоря уже о работе со многими коллегами, которые искали то же самое.
И в тех случаях, когда производительность не может быть слишком скомпрометирована в пользу производительности, усердный поиск таких решений не может привести ни к производительности, ни к производительности. Поэтому иногда полезно просто остановиться и посмотреть на природу конкретных требований к данным для программного обеспечения и посмотреть, сможем ли мы "обмануть" и создать "адаптированные", более узко применимые решения в соответствии с этими специфическими требованиями, как в этом примере. Иногда это самый полезный способ получить хорошее сочетание производительности и производительности в тех случаях, когда один не может быть слишком скомпрометирован в пользу другого.
4. Java IntList
Я надеюсь, что люди не возражают против того, чтобы я опубликовал третий ответ, но я снова исчерпал лимит персонажей. Я закончил портирование кода C во втором ответе на Java. Порт Java может быть проще для людей, портирующих на объектно-ориентированные языки.
class IntList
{
private int data[] = new int[128];
private int num_fields = 0;
private int num = 0;
private int cap = 128;
private int free_element = -1;
// Creates a new list of elements which each consist of integer fields.
// 'start_num_fields' specifies the number of integer fields each element has.
public IntList(int start_num_fields)
{
num_fields = start_num_fields;
}
// Returns the number of elements in the list.
int size()
{
return num;
}
// Returns the value of the specified field for the nth element.
int get(int n, int field)
{
assert n >= 0 && n < num && field >= 0 && field < num_fields;
return data[n*num_fields + field];
}
// Sets the value of the specified field for the nth element.
void set(int n, int field, int val)
{
assert n >= 0 && n < num && field >= 0 && field < num_fields;
data[n*num_fields + field] = val;
}
// Clears the list, making it empty.
void clear()
{
num = 0;
free_element = -1;
}
// Inserts an element to the back of the list and returns an index to it.
int pushBack()
{
final int new_pos = (num+1) * num_fields;
// If the list is full, we need to reallocate the buffer to make room
// for the new element.
if (new_pos > cap)
{
// Use double the size for the new capacity.
final int new_cap = new_pos * 2;
// Allocate new array and copy former contents.
int new_array[] = new int[new_cap];
System.arraycopy(data, 0, new_array, 0, cap);
data = new_array;
// Set the old capacity to the new capacity.
cap = new_cap;
}
return num++;
}
// Removes the element at the back of the list.
void popBack()
{
// Just decrement the list size.
assert num > 0;
--num;
}
// Inserts an element to a vacant position in the list and returns an index to it.
int insert()
{
// If there's a free index in the free list, pop that and use it.
if (free_element != -1)
{
final int index = free_element;
final int pos = index * num_fields;
// Set the free index to the next free index.
free_element = data[pos];
// Return the free index.
return index;
}
// Otherwise insert to the back of the array.
return pushBack();
}
// Removes the nth element in the list.
void erase(int n)
{
// Push the element to the free list.
final int pos = n * num_fields;
data[pos] = free_element;
free_element = n;
}
}
Java Quadtree
А вот и quadtree в Java (извините, если он не очень идиоматичен; я не писал Java около десяти лет и забыл много вещей):
interface IQtVisitor
{
// Called when traversing a branch node.
// (mx, my) indicate the center of the node's AABB.
// (sx, sy) indicate the half-size of the node's AABB.
void branch(Quadtree qt, int node, int depth, int mx, int my, int sx, int sy);
// Called when traversing a leaf node.
// (mx, my) indicate the center of the node's AABB.
// (sx, sy) indicate the half-size of the node's AABB.
void leaf(Quadtree qt, int node, int depth, int mx, int my, int sx, int sy);
}
class Quadtree
{
// Creates a quadtree with the requested extents, maximum elements per leaf, and maximum tree depth.
Quadtree(int width, int height, int start_max_elements, int start_max_depth)
{
max_elements = start_max_elements;
max_depth = start_max_depth;
// Insert the root node to the qt.
nodes.insert();
nodes.set(0, node_idx_fc, -1);
nodes.set(0, node_idx_num, 0);
// Set the extents of the root node.
root_mx = width / 2;
root_my = height / 2;
root_sx = root_mx;
root_sy = root_my;
}
// Outputs a list of elements found in the specified rectangle.
public int insert(int id, float x1, float y1, float x2, float y2)
{
// Insert a new element.
final int new_element = elts.insert();
// Set the fields of the new element.
elts.set(new_element, elt_idx_lft, floor_int(x1));
elts.set(new_element, elt_idx_top, floor_int(y1));
elts.set(new_element, elt_idx_rgt, floor_int(x2));
elts.set(new_element, elt_idx_btm, floor_int(y2));
elts.set(new_element, elt_idx_id, id);
// Insert the element to the appropriate leaf node(s).
node_insert(0, 0, root_mx, root_my, root_sx, root_sy, new_element);
return new_element;
}
// Removes the specified element from the tree.
public void remove(int element)
{
// Find the leaves.
final int lft = elts.get(element, elt_idx_lft);
final int top = elts.get(element, elt_idx_top);
final int rgt = elts.get(element, elt_idx_rgt);
final int btm = elts.get(element, elt_idx_btm);
IntList leaves = find_leaves(0, 0, root_mx, root_my, root_sx, root_sy, lft, top, rgt, btm);
// For each leaf node, remove the element node.
for (int j=0; j < leaves.size(); ++j)
{
final int nd_index = leaves.get(j, nd_idx_index);
// Walk the list until we find the element node.
int node_index = nodes.get(nd_index, node_idx_fc);
int prev_index = -1;
while (node_index != -1 && enodes.get(node_index, enode_idx_elt) != element)
{
prev_index = node_index;
node_index = enodes.get(node_index, enode_idx_next);
}
if (node_index != -1)
{
// Remove the element node.
final int next_index = enodes.get(node_index, enode_idx_next);
if (prev_index == -1)
nodes.set(nd_index, node_idx_fc, next_index);
else
enodes.set(prev_index, enode_idx_next, next_index);
enodes.erase(node_index);
// Decrement the leaf element count.
nodes.set(nd_index, node_idx_num, nodes.get(nd_index, node_idx_num)-1);
}
}
// Remove the element.
elts.erase(element);
}
// Cleans up the tree, removing empty leaves.
public void cleanup()
{
IntList to_process = new IntList(1);
// Only process the root if it's not a leaf.
if (nodes.get(0, node_idx_num) == -1)
{
// Push the root index to the stack.
to_process.set(to_process.pushBack(), 0, 0);
}
while (to_process.size() > 0)
{
// Pop a node from the stack.
final int node = to_process.get(to_process.size()-1, 0);
final int fc = nodes.get(node, node_idx_fc);
int num_empty_leaves = 0;
to_process.popBack();
// Loop through the children.
for (int j=0; j < 4; ++j)
{
final int child = fc + j;
// Increment empty leaf count if the child is an empty
// leaf. Otherwise if the child is a branch, add it to
// the stack to be processed in the next iteration.
if (nodes.get(child, node_idx_num) == 0)
++num_empty_leaves;
else if (nodes.get(child, node_idx_num) == -1)
{
// Push the child index to the stack.
to_process.set(to_process.pushBack(), 0, child);
}
}
// If all the children were empty leaves, remove them and
// make this node the new empty leaf.
if (num_empty_leaves == 4)
{
// Remove all 4 children in reverse order so that they
// can be reclaimed on subsequent insertions in proper
// order.
nodes.erase(fc + 3);
nodes.erase(fc + 2);
nodes.erase(fc + 1);
nodes.erase(fc + 0);
// Make this node the new empty leaf.
nodes.set(node, node_idx_fc, -1);
nodes.set(node, node_idx_num, 0);
}
}
}
// Returns a list of elements found in the specified rectangle.
public IntList query(float x1, float y1, float x2, float y2)
{
return query(x1, y1, x2, y2, -1);
}
// Returns a list of elements found in the specified rectangle excluding the
// specified element to omit.
public IntList query(float x1, float y1, float x2, float y2, int omit_element)
{
IntList out = new IntList(1);
// Find the leaves that intersect the specified query rectangle.
final int qlft = floor_int(x1);
final int qtop = floor_int(y1);
final int qrgt = floor_int(x2);
final int qbtm = floor_int(y2);
IntList leaves = find_leaves(0, 0, root_mx, root_my, root_sx, root_sy, qlft, qtop, qrgt, qbtm);
if (temp_size < elts.size())
{
temp_size = elts.size();
temp = new boolean[temp_size];;
}
// For each leaf node, look for elements that intersect.
for (int j=0; j < leaves.size(); ++j)
{
final int nd_index = leaves.get(j, nd_idx_index);
// Walk the list and add elements that intersect.
int elt_node_index = nodes.get(nd_index, node_idx_fc);
while (elt_node_index != -1)
{
final int element = enodes.get(elt_node_index, enode_idx_elt);
final int lft = elts.get(element, elt_idx_lft);
final int top = elts.get(element, elt_idx_top);
final int rgt = elts.get(element, elt_idx_rgt);
final int btm = elts.get(element, elt_idx_btm);
if (!temp[element] && element != omit_element && intersect(qlft,qtop,qrgt,qbtm, lft,top,rgt,btm))
{
out.set(out.pushBack(), 0, element);
temp[element] = true;
}
elt_node_index = enodes.get(elt_node_index, enode_idx_next);
}
}
// Unmark the elements that were inserted.
for (int j=0; j < out.size(); ++j)
temp[out.get(j, 0)] = false;
return out;
}
// Traverses all the nodes in the tree, calling 'branch' for branch nodes and 'leaf'
// for leaf nodes.
public void traverse(IQtVisitor visitor)
{
IntList to_process = new IntList(nd_num);
pushNode(to_process, 0, 0, root_mx, root_my, root_sx, root_sy);
while (to_process.size() > 0)
{
final int back_idx = to_process.size() - 1;
final int nd_mx = to_process.get(back_idx, nd_idx_mx);
final int nd_my = to_process.get(back_idx, nd_idx_my);
final int nd_sx = to_process.get(back_idx, nd_idx_sx);
final int nd_sy = to_process.get(back_idx, nd_idx_sy);
final int nd_index = to_process.get(back_idx, nd_idx_index);
final int nd_depth = to_process.get(back_idx, nd_idx_depth);
final int fc = nodes.get(nd_index, node_idx_fc);
to_process.popBack();
if (nodes.get(nd_index, node_idx_num) == -1)
{
// Push the children of the branch to the stack.
final int hx = nd_sx >> 1, hy = nd_sy >> 1;
final int l = nd_mx-hx, t = nd_my-hx, r = nd_mx+hx, b = nd_my+hy;
pushNode(to_process, fc+0, nd_depth+1, l,t, hx,hy);
pushNode(to_process, fc+1, nd_depth+1, r,t, hx,hy);
pushNode(to_process, fc+2, nd_depth+1, l,b, hx,hy);
pushNode(to_process, fc+3, nd_depth+1, r,b, hx,hy);
visitor.branch(this, nd_index, nd_depth, nd_mx, nd_my, nd_sx, nd_sy);
}
else
visitor.leaf(this, nd_index, nd_depth, nd_mx, nd_my, nd_sx, nd_sy);
}
}
private static int floor_int(float val)
{
return (int)val;
}
private static boolean intersect(int l1, int t1, int r1, int b1,
int l2, int t2, int r2, int b2)
{
return l2 <= r1 && r2 >= l1 && t2 <= b1 && b2 >= t1;
}
private static void pushNode(IntList nodes, int nd_index, int nd_depth, int nd_mx, int nd_my, int nd_sx, int nd_sy)
{
final int back_idx = nodes.pushBack();
nodes.set(back_idx, nd_idx_mx, nd_mx);
nodes.set(back_idx, nd_idx_my, nd_my);
nodes.set(back_idx, nd_idx_sx, nd_sx);
nodes.set(back_idx, nd_idx_sy, nd_sy);
nodes.set(back_idx, nd_idx_index, nd_index);
nodes.set(back_idx, nd_idx_depth, nd_depth);
}
private IntList find_leaves(int node, int depth,
int mx, int my, int sx, int sy,
int lft, int top, int rgt, int btm)
{
IntList leaves = new IntList(nd_num);
IntList to_process = new IntList(nd_num);
pushNode(to_process, node, depth, mx, my, sx, sy);
while (to_process.size() > 0)
{
final int back_idx = to_process.size() - 1;
final int nd_mx = to_process.get(back_idx, nd_idx_mx);
final int nd_my = to_process.get(back_idx, nd_idx_my);
final int nd_sx = to_process.get(back_idx, nd_idx_sx);
final int nd_sy = to_process.get(back_idx, nd_idx_sy);
final int nd_index = to_process.get(back_idx, nd_idx_index);
final int nd_depth = to_process.get(back_idx, nd_idx_depth);
to_process.popBack();
// If this node is a leaf, insert it to the list.
if (nodes.get(nd_index, node_idx_num) != -1)
pushNode(leaves, nd_index, nd_depth, nd_mx, nd_my, nd_sx, nd_sy);
else
{
// Otherwise push the children that intersect the rectangle.
final int fc = nodes.get(nd_index, node_idx_fc);
final int hx = nd_sx / 2, hy = nd_sy / 2;
final int l = nd_mx-hx, t = nd_my-hx, r = nd_mx+hx, b = nd_my+hy;
if (top <= nd_my)
{
if (lft <= nd_mx)
pushNode(to_process, fc+0, nd_depth+1, l,t,hx,hy);
if (rgt > nd_mx)
pushNode(to_process, fc+1, nd_depth+1, r,t,hx,hy);
}
if (btm > nd_my)
{
if (lft <= nd_mx)
pushNode(to_process, fc+2, nd_depth+1, l,b,hx,hy);
if (rgt > nd_mx)
pushNode(to_process, fc+3, nd_depth+1, r,b,hx,hy);
}
}
}
return leaves;
}
private void node_insert(int index, int depth, int mx, int my, int sx, int sy, int element)
{
// Find the leaves and insert the element to all the leaves found.
final int lft = elts.get(element, elt_idx_lft);
final int top = elts.get(element, elt_idx_top);
final int rgt = elts.get(element, elt_idx_rgt);
final int btm = elts.get(element, elt_idx_btm);
IntList leaves = find_leaves(index, depth, mx, my, sx, sy, lft, top, rgt, btm);
for (int j=0; j < leaves.size(); ++j)
{
final int nd_mx = leaves.get(j, nd_idx_mx);
final int nd_my = leaves.get(j, nd_idx_my);
final int nd_sx = leaves.get(j, nd_idx_sx);
final int nd_sy = leaves.get(j, nd_idx_sy);
final int nd_index = leaves.get(j, nd_idx_index);
final int nd_depth = leaves.get(j, nd_idx_depth);
leaf_insert(nd_index, nd_depth, nd_mx, nd_my, nd_sx, nd_sy, element);
}
}
private void leaf_insert(int node, int depth, int mx, int my, int sx, int sy, int element)
{
// Insert the element node to the leaf.
final int nd_fc = nodes.get(node, node_idx_fc);
nodes.set(node, node_idx_fc, enodes.insert());
enodes.set(nodes.get(node, node_idx_fc), enode_idx_next, nd_fc);
enodes.set(nodes.get(node, node_idx_fc), enode_idx_elt, element);
// If the leaf is full, split it.
if (nodes.get(node, node_idx_num) == max_elements && depth < max_depth)
{
// Transfer elements from the leaf node to a list of elements.
IntList elts = new IntList(1);
while (nodes.get(node, node_idx_fc) != -1)
{
final int index = nodes.get(node, node_idx_fc);
final int next_index = enodes.get(index, enode_idx_next);
final int elt = enodes.get(index, enode_idx_elt);
// Pop off the element node from the leaf and remove it from the qt.
nodes.set(node, node_idx_fc, next_index);
enodes.erase(index);
// Insert element to the list.
elts.set(elts.pushBack(), 0, elt);
}
// Start by allocating 4 child nodes.
final int fc = nodes.insert();
nodes.insert();
nodes.insert();
nodes.insert();
nodes.set(node, node_idx_fc, fc);
// Initialize the new child nodes.
for (int j=0; j < 4; ++j)
{
nodes.set(fc+j, node_idx_fc, -1);
nodes.set(fc+j, node_idx_num, 0);
}
// Transfer the elements in the former leaf node to its new children.
nodes.set(node, node_idx_num, -1);
for (int j=0; j < elts.size(); ++j)
node_insert(node, depth, mx, my, sx, sy, elts.get(j, 0));
}
else
{
// Increment the leaf element count.
nodes.set(node, node_idx_num, nodes.get(node, node_idx_num) + 1);
}
}
// ----------------------------------------------------------------------------------------
// Element node fields:
// ----------------------------------------------------------------------------------------
// Points to the next element in the leaf node. A value of -1
// indicates the end of the list.
static final int enode_idx_next = 0;
// Stores the element index.
static final int enode_idx_elt = 1;
// Stores all the element nodes in the quadtree.
private IntList enodes = new IntList(2);
// ----------------------------------------------------------------------------------------
// Element fields:
// ----------------------------------------------------------------------------------------
// Stores the rectangle encompassing the element.
static final int elt_idx_lft = 0, elt_idx_top = 1, elt_idx_rgt = 2, elt_idx_btm = 3;
// Stores the ID of the element.
static final int elt_idx_id = 4;
// Stores all the elements in the quadtree.
private IntList elts = new IntList(5);
// ----------------------------------------------------------------------------------------
// Node fields:
// ----------------------------------------------------------------------------------------
// Points to the first child if this node is a branch or the first element
// if this node is a leaf.
static final int node_idx_fc = 0;
// Stores the number of elements in the node or -1 if it is not a leaf.
static final int node_idx_num = 1;
// Stores all the nodes in the quadtree. The first node in this
// sequence is always the root.
private IntList nodes = new IntList(2);
// ----------------------------------------------------------------------------------------
// Node data fields:
// ----------------------------------------------------------------------------------------
static final int nd_num = 6;
// Stores the extents of the node using a centered rectangle and half-size.
static final int nd_idx_mx = 0, nd_idx_my = 1, nd_idx_sx = 2, nd_idx_sy = 3;
// Stores the index of the node.
static final int nd_idx_index = 4;
// Stores the depth of the node.
static final int nd_idx_depth = 5;
// ----------------------------------------------------------------------------------------
// Data Members
// ----------------------------------------------------------------------------------------
// Temporary buffer used for queries.
private boolean temp[];
// Stores the size of the temporary buffer.
private int temp_size = 0;
// Stores the quadtree extents.
private int root_mx, root_my, root_sx, root_sy;
// Maximum allowed elements in a leaf before the leaf is subdivided/split unless
// the leaf is at the maximum allowed tree depth.
private int max_elements;
// Stores the maximum depth allowed for the quadtree.
private int max_depth;
}
Временное заключение
Снова извините, это немного ответ дампа кода. Я вернусь и отредактирую это и попытаюсь объяснить все больше и больше вещей.
Пожалуйста, обратитесь к исходному ответу для получения подробной информации об общем подходе.