Расчет результирующего вектора скорости после двумерного столкновения

Question

В настоящее время у меня есть мини-физическая игра, которая использует теорему о разделении осей для обнаружения столкновений и реагирования на них, однако я зашел в тупик, когда обнаружил, что не было много документации о том, что происходит со скоростью объекта после его столкновения с другой формой с использованием столкновения SAT обнаружение.

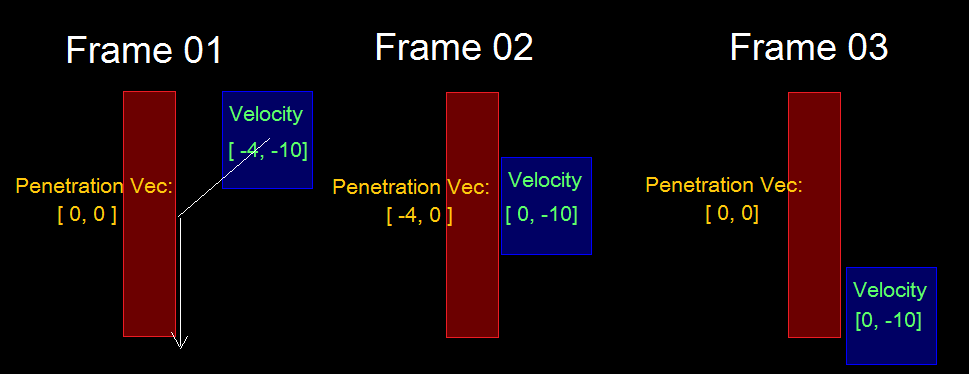
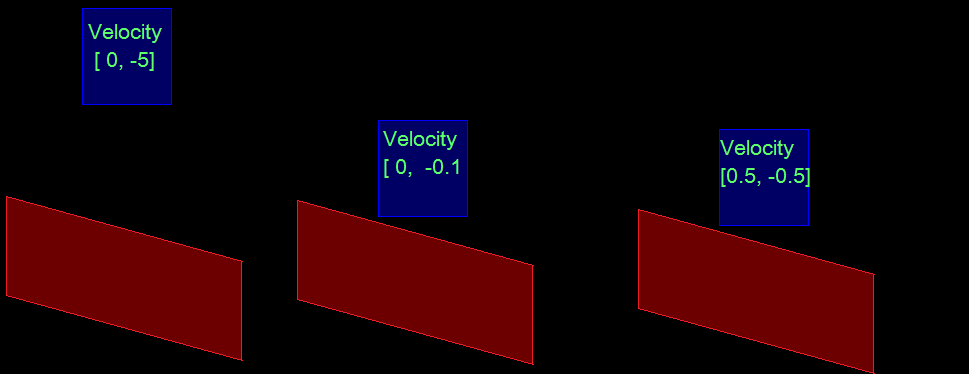
Вот две диаграммы того, о чем я говорю.

Кто-нибудь может указать мне правильное направление, пожалуйста?

Вся информация, которая может быть предоставлена ​​после столкновения, является минимальным вектором проникновения.

РЕДАКТИРОВАТЬ: нашел какой-то код в Интернете, который очень связан с этим, но я не понимаю:

void CBody::ProcessCollision(CBody& xBody, const Vector& N, float t)
{
    Vector D = m_xDisplacement - xBody.m_xDisplacement;

    float n  = D * N;

    Vector Dn = N * n;
    Vector Dt = D - Dn;

    if (n > 0.0f) Dn = Vector(0, 0);

    float dt  = Dt * Dt;
    float CoF = s_fFriction;

    if (dt < s_fGlue*s_fGlue) CoF = 1.01f;

    D = -(1.0f + s_fRestitution) * Dn - (CoF) * Dt;

    float m0 =       GetInvMass();
    float m1 = xBody.GetInvMass();
    float m  = m0 + m1;
    float r0 = m0 / m;
    float r1 = m1 / m;

          m_xDisplacement += D * r0;
    xBody.m_xDisplacement -= D * r1;
}

Answer 1

Обнаружение столкновений и как справляться со столкновениями - это две разные вещи.

Что происходит после столкновения, зависит от того, какую физику вы пытаетесь достичь.

Например, на вашем верхнем рисунке давайте предположим, что красная часть - это неподвижная стена, и движется только синяя часть. Вектор движения синей фигуры уже разделен на ортогональные части, параллельные и перпендикулярные поверхности красной стены. Простым способом обработки столкновений в этом случае было бы просто перевернуть компонент вектора скорости перпендикулярно стене. Таким образом, вектор [-4, 10] станет [4,10].