Эффективная выборка коллекции мультинормальных переменных с изменяющейся сигма (ковариационной) матрицей

Question

Я новичок в Стэн, так что надеюсь, что вы можете указать мне в правильном направлении. Я создам ситуацию, чтобы убедиться, что мы на одной странице...

Если бы у меня была коллекция одномерных нормалей, документы сказали бы мне, что:

y ~ normal(mu_vec, sigma);

предоставляет ту же модель, что и невекторизованная версия:

for (n in 1:N)
    y[n] ~ normal(mu_vec[n], sigma);

но что векторизованная версия (намного?) быстрее. Хорошо, хорошо, имеет смысл.

Итак, первый вопрос: возможно ли воспользоваться этим ускорением векторизации в одномерном нормальном случае, когда оба mu а также sigma образцов различаются по положению в векторе. Т.е. если оба mu_vec а также sigma_vec являются векторами (в предыдущем случае sigma был скаляр), то это:

y ~ normal(mu_vec, sigma_vec);

эквивалентно этому:

for (n in 1:N)
    y[n] ~ normal(mu_vec[n], sigma_vec[n]);

и если да, то есть ли сопоставимое ускорение?

Хорошо. Это разминка. Реальный вопрос заключается в том, как наилучшим образом приблизиться к многовариантному эквиваленту вышеизложенного.

В моем конкретном случае у меня есть N наблюдений двумерных данных для некоторой переменной y, который я храню в N x 2 матрица. (Для порядка величины N около 1000 в моем случае использования.)

Я считаю, что среднее значение каждого компонента каждого наблюдения 0 и что stdev каждого компонента каждого наблюдения 1 (и я рад жестко закодировать их как таковые). Тем не менее, я считаю, что корреляция (rho) изменяется от наблюдения к наблюдению как (простая) функция другой наблюдаемой переменной, x (хранится в N элемент вектора). Например, мы могли бы сказать, что rho[n] = 2*inverse_logit(beta * x[n]) - 1 за n in 1:N и наша цель - узнать о beta из наших данных. Т.е. ковариационная матрица для nЭто наблюдение будет:

[1,      rho[n]]
[rho[n], 1     ]

Мой вопрос заключается в том, каков наилучший способ соединить это в модели STAN, чтобы она не была слишком медленной? Есть ли векторизованная версия multi_normal распределение, чтобы я мог указать это как:

y ~ multi_normal(vector_of_mu_2_tuples, vector_of_sigma_matrices)

или, может быть, как некоторые другие подобные формулировки? Или мне нужно будет написать:

for (n in 1:N)
    y[n] ~ multi_normal(vector_of_mu_2_tuples[n], vector_of_sigma_matrices[n])

после настройки vector_of_sigma_matrices а также vector_of_mu_2_tuples в более раннем блоке?

Заранее спасибо за любое руководство!

---

Изменить, чтобы добавить код

Используя python, я могу генерировать данные в духе моей проблемы следующим образом:

import numpy as np
import pandas as pd
import pystan as pys
import scipy as sp
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1 import make_axes_locatable
import seaborn as sns

def gen_normal_data(N, true_beta, true_mu, true_stdevs):
    N = N

    true_beta = true_beta
    true_mu = true_mu
    true_stdevs = true_stdevs

    drivers = np.random.randn(N)
    correls = 2.0 * sp.special.expit(drivers*true_beta)-1.0

    observations = []
    for i in range(N):
        covar = np.array([[true_stdevs[0]**2, true_stdevs[0] * true_stdevs[1] * correls[i]],
                          [true_stdevs[0] * true_stdevs[1] * correls[i], true_stdevs[1]**2]])
        observations.append(sp.stats.multivariate_normal.rvs(true_mu, covar, size=1).tolist())
    observations = np.array(observations)

    return {
        'N': N,
        'true_mu': true_mu,
        'true_stdev': true_stdevs,
        'y': observations,
        'd': drivers,
        'correls': correls
    }

а затем фактически сгенерировать данные, используя:

normal_data = gen_normal_data(100, 1.5, np.array([1., 5.]), np.array([2., 5.]))

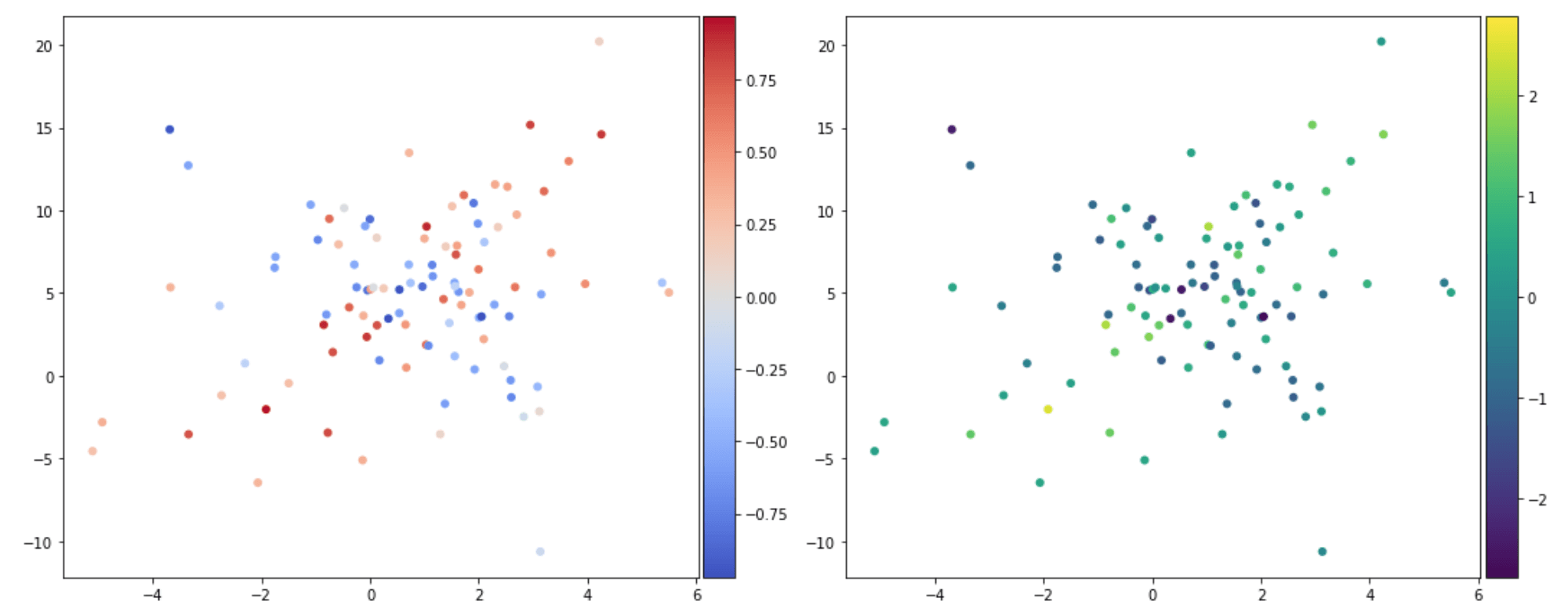
Вот как выглядит набор данных (график рассеяния y окрашен correls в левой панели и drivers в правой панели... так что идея заключается в том, что чем выше driver ближе к 1 correl и ниже driverчем ближе к -1 correl, Таким образом, можно ожидать, что красные точки на левой панели будут "сверху вниз слева направо", а синие точки "вверх слева направо вниз", и на самом деле это:

fig, axes = plt.subplots(1, 2, figsize=(15, 6))
x = normal_data['y'][:, 0]
y = normal_data['y'][:, 1]
correls = normal_data['correls']
drivers = normal_data['d']

for ax, colordata, cmap in zip(axes, [correls, drivers], ['coolwarm', 'viridis']):
    color_extreme = max(abs(colordata.max()), abs(colordata.min()))
    sc = ax.scatter(x, y, c=colordata, lw=0, cmap=cmap, vmin=-color_extreme, vmax=color_extreme)
    divider = make_axes_locatable(ax)
    cax = divider.append_axes('right', size='5%', pad=0.05)
    fig.colorbar(sc, cax=cax, orientation='vertical')
fig.tight_layout()

Используя метод грубой силы, я могу настроить модель STAN, которая выглядит следующим образом:

model_naked = pys.StanModel(
    model_name='naked',
    model_code="""
data {
    int<lower=0> N;
    vector[2] true_mu;
    vector[2] true_stdev;
    real d[N];
    vector[2] y[N];
}

parameters {
    real beta;
}

transformed parameters {
}

model {
    real rho[N];
    matrix[2, 2] cov[N];

    for (n in 1:N) {
        rho[n] = 2.0*inv_logit(beta * d[n]) - 1.0;

        cov[n, 1, 1] = true_stdev[1]^2;
        cov[n, 1, 2] = true_stdev[1] * true_stdev[2] * rho[n];
        cov[n, 2, 1] = true_stdev[1] * true_stdev[2] * rho[n];
        cov[n, 2, 2] = true_stdev[2]^2;
    }

    beta ~ normal(0, 10000);
    for (n in 1:N) {
        y[n] ~ multi_normal(true_mu, cov[n]);
    }
}
"""
)

Это подходит красиво:

fit_naked = model_naked.sampling(data=normal_data, iter=1000, chains=2)f = fit_naked.plot();
f.tight_layout()

Но я надеюсь, что кто-то может указать мне правильное направление для "маргинализованного" подхода, в котором мы разбиваем наш двумерный нормаль на пару независимых нормалей, которые можно смешать, используя корреляцию. Причина, по которой я нуждаюсь в этом, заключается в том, что в моем реальном случае использования оба аспекта имеют толстый хвост. Я счастлив смоделировать это как студенческий дистрибутив, но проблема в том, что STAN позволяет только один nu должен быть указан (не один для каждого измерения), поэтому я думаю, что мне нужно найти способ разложить multi_student_t в пару независимых student_tтак что я могу установить степени свободы отдельно для каждого измерения.

Answer 1

Одномерное нормальное распределение принимает векторы для любого или всех своих аргументов, и это будет быстрее, чем зацикливание N Наблюдения, чтобы назвать это N раз со скалярными аргументами.

Тем не менее, ускорение будет только линейным, потому что все вычисления одинаковы, но ему нужно только выделить память один раз, если вы вызываете ее только один раз. Общее время ожидания в большей степени зависит от количества выполняемых функций, которые вы должны выполнить. 2^10 - 1 на итерацию MCMC (по умолчанию), но то, достигнете ли вы максимальной глубины дерева, зависит от геометрии апостериорного распределения, из которого вы пытаетесь выбрать, что, в свою очередь, зависит от всего, включая данные, которые вы обрабатываете.

Двустороннее нормальное распределение может быть записано как произведение предельного одномерного нормального распределения для первой переменной и условного одномерного нормального распределения для второй переменной с учетом первой переменной. В коде Stan мы можем использовать поэлементное умножение и деление, чтобы записать его плотность записи как

target += normal_lpdf(first_variable | first_means, first_sigmas);
target += normal_lpdf(second_variable | second_means + 
  rhos .* first_sigmas ./ second_sigmas .* (first_variable - first_means),
  second_sigmas .* sqrt(1 - square(rhos)));

К сожалению, более общее многомерное нормальное распределение в Stan не имеет реализации, которая вводит массивы ковариационных матриц.

Answer 2

Это не совсем отвечает на ваш вопрос, но вы можете сделать вашу программу более эффективной, удалив кучу избыточных вычислений и немного преобразовав масштаб, чтобы использовать tanh, а не масштабированный обратный логит. Я бы избавился от масштабирования и просто использовал меньшие бета-версии, но я оставил его, чтобы он получал те же результаты.

data {
  int<lower=0> N;
  vector[2] mu;
  vector[2] sigma;
  vector[N] d;
  vector[2] y[N];
}
parameters {
  real beta;
}
transformed data {
  real var1 = square(sigma[1]);
  real var2 = square(sigma[2]);
  real covar12 = sigma[1] * sigma[2];
  vector[N] d_div_2 = d * 0.5;
}
model {
  // note: tanh(u) = 2 * inv_logit(u / 2) - 1
  vector[N] rho = tanh(beta * d_div_2);
  matrix[2, 2] Sigma;
  Sigma[1, 1] = var1;
  Sigma[2, 2] = var2;
  // only reassign what's necessary with minimal recomputation
  for (n in 1:N) {
    Sigma[1, 2] = rho[n] * covar12;
    Sigma[2, 1] = Sigma[1, 2];
    y[n] ~ multi_normal(true_mu, Sigma);
  }
  // weakly informative priors fit more easily
  beta ~ normal(0, 8);
}

Вы также можете учесть, вычислив факторизацию Холецкого как функцию rho и другие фиксированные значения и используйте это --- это сохраняет решающий шаг в многомерной нормали.

Другой вариант, который у вас есть, это записать multi-student-t напрямую, а не использовать нашу встроенную реализацию. Встроенная функция, вероятно, не будет намного быстрее, так как матрица решает все операции.