Равномерно распределяя n точек по сфере
Мне нужен алгоритм, который может дать мне позиции вокруг сферы для N точек (вероятно, меньше 20), которые расплывчато распределяют их. Нет необходимости в "совершенстве", но мне просто нужно, чтобы ни один из них не был сгруппирован вместе.
- Этот вопрос предоставил хороший код, но я не смог найти способ сделать это униформой, так как это казалось на 100% рандомизированным.
- Этот рекомендованный пост в блоге имел два способа, позволяющих вводить количество точек на сфере, но алгоритм Saff и Kuijlaars находится именно в psuedocode, который я мог бы транскрибировать, и найденный мной пример кода содержал "node[k]", который я не смог см. объяснил и разрушил эту возможность. Второй пример блога - "Спираль золотого сечения", которая дала мне странные, сгруппированные результаты без четкого способа определения постоянного радиуса.
- Кажется, что этот алгоритм из этого вопроса может сработать, но я не могу собрать воедино то, что находится на этой странице, в psuedocode или что-то еще.
Несколько других вопросов, с которыми я сталкивался, говорили о рандомизированном равномерном распределении, что добавляет уровень сложности, который меня не беспокоит. Я прошу прощения за то, что это такой глупый вопрос, но я хотел показать, что я действительно выглядел суровым и все еще терпел неудачу.
Итак, я ищу простой псевдокод для равномерного распределения N точек вокруг единичной сферы, который возвращает либо сферические, либо декартовы координаты. Еще лучше, если он может даже распределяться с небольшим количеством рандомизации (подумайте, планеты вокруг звезды, прилично распределены, но есть место для свободы).
18 ответов
В этом примере кода node[k] это просто k-й узел. Вы генерируете массив N точек и node[k] является kth (от 0 до N-1). Если это все, что вас смущает, надеюсь, вы можете использовать это сейчас.
(другими словами, k является массивом размера N, который определяется до запуска фрагмента кода и который содержит список точек).
В качестве альтернативы, опираясь на другой ответ здесь (и используя Python):
> cat ll.py
from math import asin
nx = 4; ny = 5
for x in range(nx):
lon = 360 * ((x+0.5) / nx)
for y in range(ny):
midpt = (y+0.5) / ny
lat = 180 * asin(2*((y+0.5)/ny-0.5))
print lon,lat
> python2.7 ll.py
45.0 -166.91313924
45.0 -74.0730322921
45.0 0.0
45.0 74.0730322921
45.0 166.91313924
135.0 -166.91313924
135.0 -74.0730322921
135.0 0.0
135.0 74.0730322921
135.0 166.91313924
225.0 -166.91313924
225.0 -74.0730322921
225.0 0.0
225.0 74.0730322921
225.0 166.91313924
315.0 -166.91313924
315.0 -74.0730322921
315.0 0.0
315.0 74.0730322921
315.0 166.91313924
Если вы построите это, вы увидите, что вертикальный интервал больше у полюсов, так что каждая точка находится примерно на одной и той же общей площади пространства (около полюсов меньше места "по горизонтали", поэтому он дает больше "по вертикали").).
Это не то же самое, что все точки, находящиеся примерно на одинаковом расстоянии от своих соседей (о чем, я думаю, говорят ваши ссылки), но этого может быть достаточно для того, что вы хотите, и улучшается просто создание равномерной широты и долготы.,
Алгоритм сферы Фибоначчи отлично подходит для этого. Это быстро и дает результаты, которые с первого взгляда легко обмануть человеческий глаз. Вы можете увидеть пример с обработкой, который покажет результат с течением времени по мере добавления точек. Вот еще один отличный интерактивный пример, сделанный @gman. А вот быстрая версия на Python с простой опцией рандомизации:
import math, random
def fibonacci_sphere(samples=1,randomize=True):
rnd = 1.
if randomize:
rnd = random.random() * samples
points = []
offset = 2./samples
increment = math.pi * (3. - math.sqrt(5.));
for i in range(samples):
y = ((i * offset) - 1) + (offset / 2);
r = math.sqrt(1 - pow(y,2))
phi = ((i + rnd) % samples) * increment
x = math.cos(phi) * r
z = math.sin(phi) * r
points.append([x,y,z])
return points
1000 образцов дает вам это:
Метод золотой спирали
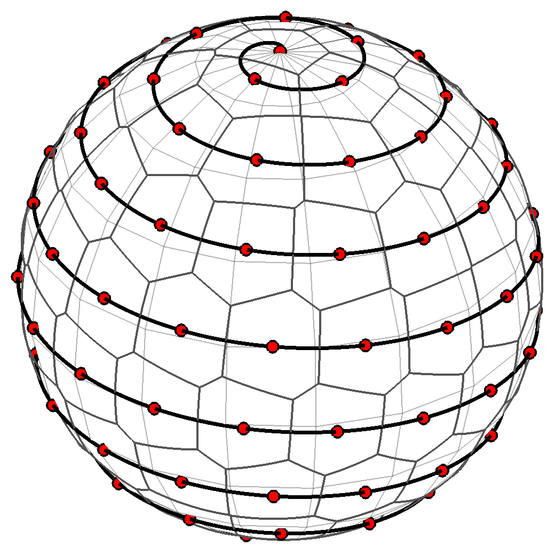
Вы сказали, что не можете заставить метод золотой спирали работать, и это позор, потому что это действительно очень хорошо. Я хотел бы дать вам полное понимание этого, так что, возможно, вы сможете понять, как не допустить, чтобы это было "сгруппировано".
Так что вот быстрый, неслучайный способ создать решетку, которая будет приблизительно правильной; как обсуждалось выше, ни одна решетка не будет идеальной, но это может быть "достаточно хорошо". Он сравнивается с другими методами, например, на BendWavy.org, но у него просто красивый внешний вид, а также гарантия равномерного интервала в пределах.
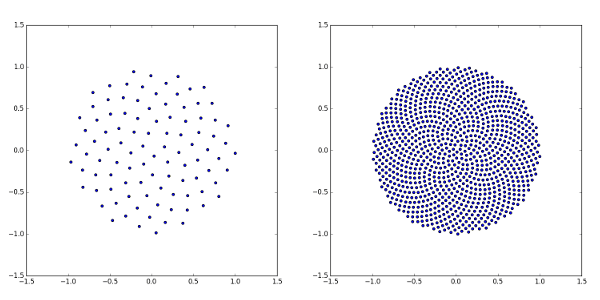
Грунтовка: спирали подсолнуха на диске агрегата
Чтобы понять этот алгоритм, я сначала приглашаю вас взглянуть на алгоритм спирали 2D подсолнечника. Это основано на том факте, что самым иррациональным числом является золотое сечение (1 + sqrt(5))/2 и если кто-то испускает точки при подходе "стоять в центре, повернуть золотое сечение целых оборотов, а затем испустить другую точку в этом направлении", он, естественно, создает спираль, которая, как вы получаете все большее и большее количество точек, тем не менее отказывается иметь четко определенные "бары", на которых выстраиваются точки.(Примечание 1.)
Алгоритм равномерного разнесения на диске,
from numpy import pi, cos, sin, sqrt, arange
import matplotlib.pyplot as pp
num_pts = 100
indices = arange(0, num_pts, dtype=float) + 0.5
r = sqrt(indices/num_pts)
theta = pi * (1 + 5**0.5) * indices
pp.scatter(r*cos(theta), r*sin(theta))
pp.show()
и это дает результаты, которые выглядят как (n=100 и n=1000):
Расстояние между точками радиально
Ключевая странная вещь - формула r = sqrt(indices / num_pts); как я дошел до этого? (Заметка 2.)
Ну, я использую здесь квадратный корень, потому что я хочу, чтобы они имели равномерное пространство вокруг сферы. Это то же самое, что сказать, что в пределе больших N я хочу, чтобы маленькая область R ∈ (r, r + dr), Θ ∈ (θ, θ + dθ) содержала количество точек, пропорциональных ее площади, что это r dr dθ. Теперь, если мы притворимся, что речь идет о случайной переменной, это имеет прямую интерпретацию, заключающуюся в том, что совместная плотность вероятности для (R, Θ) просто равна cr для некоторой постоянной c. Нормализация на единичном диске тогда заставляет c = 1 / π.
Теперь позвольте мне представить трюк. Это происходит из теории вероятностей, где она называется выборкой обратного CDF: предположим, что вы хотите сгенерировать случайную переменную с плотностью вероятности f(z), и у вас есть случайная переменная U ~ Uniform (0, 1), как и в random() в большинстве языков программирования. Как ты это делаешь?
- Во-первых, превратите вашу плотность в накопительную функцию распределения F(z), которая, помните, монотонно возрастает от 0 до 1 с производной f(z).
- Затем вычислите обратную функцию CDF F-1(z).
- Вы обнаружите, что Z = F-1(U) распределяется в соответствии с целевой плотностью. (Заметка 3).
Теперь спиральный трюк с золотым сечением расставляет точки в равномерно равномерной последовательности для θ, так что давайте интегрируем это; для единичного круга мы остаемся с F(r) = r2. Таким образом, обратная функция F-1(u) = u1/2, и, следовательно, мы будем генерировать случайные точки на сфере в полярных координатах с r = sqrt(random()); theta = 2 * pi * random(),
Теперь вместо случайной выборки этой обратной функции мы равномерно выбираем ее, и хорошая вещь в равномерной выборке состоит в том, что наши результаты о том, как точки распределены в пределе большого N, будут вести себя так, как если бы мы случайным образом выбрали его. Эта комбинация - хитрость. Вместо random() мы используем (arange(0, num_pts, dtype=float) + 0.5)/num_ptsтак что, скажем, если мы хотим, чтобы взять 10 точек, они r = 0.05, 0.15, 0.25, ... 0.95, Мы равномерно выбираем r, чтобы получить интервал равной площади, и мы используем приращение подсолнечника, чтобы избежать ужасных "полос" точек на выходе.
Сейчас занимаюсь подсолнухом на шаре
Изменения, которые нам нужно внести, чтобы расставить точки с шаром, просто включают в себя переключение полярных координат на сферические. Радиальная координата, конечно, не входит в это, потому что мы находимся на единичной сфере. Чтобы здесь все было более согласованно, хотя я и был физиком, я буду использовать координаты математиков, где 0 ≤ φ ≤ π - широта, спускающаяся с полюса, а 0 ≤ θ ≤ 2π - долгота. Таким образом, отличие от вышеизложенного состоит в том, что мы в основном заменяем переменную r на φ.
Наш элемент площади, который был r dr dθ, теперь становится не намного более сложным грехом (φ) dφ dθ. Таким образом, наша общая плотность для равномерного расстояния равна sin (φ) / 4π. Интегрируя из θ, находим f(φ) = sin (φ) / 2, поэтому F(φ) = (1 - cos (φ)) / 2. Обращая это, мы можем видеть, что равномерная случайная величина будет выглядеть как acos (1 - 2 u), но мы выбираем равномерно, а не случайно, поэтому вместо этого мы используем φk = acos (1 - 2 (k + 0,5) /N). А остальная часть алгоритма просто проецирует это на координаты x, y и z:
from numpy import pi, cos, sin, arccos, arange
import mpl_toolkits.mplot3d
import matplotlib.pyplot as pp
num_pts = 1000
indices = arange(0, num_pts, dtype=float) + 0.5
phi = arccos(1 - 2*indices/num_pts)
theta = pi * (1 + 5**0.5) * indices
x, y, z = cos(theta) * sin(phi), sin(theta) * sin(phi), cos(phi);
pp.figure().add_subplot(111, projection='3d').scatter(x, y, z);
pp.show()
Снова для n = 100 и n = 1000 результаты выглядят так: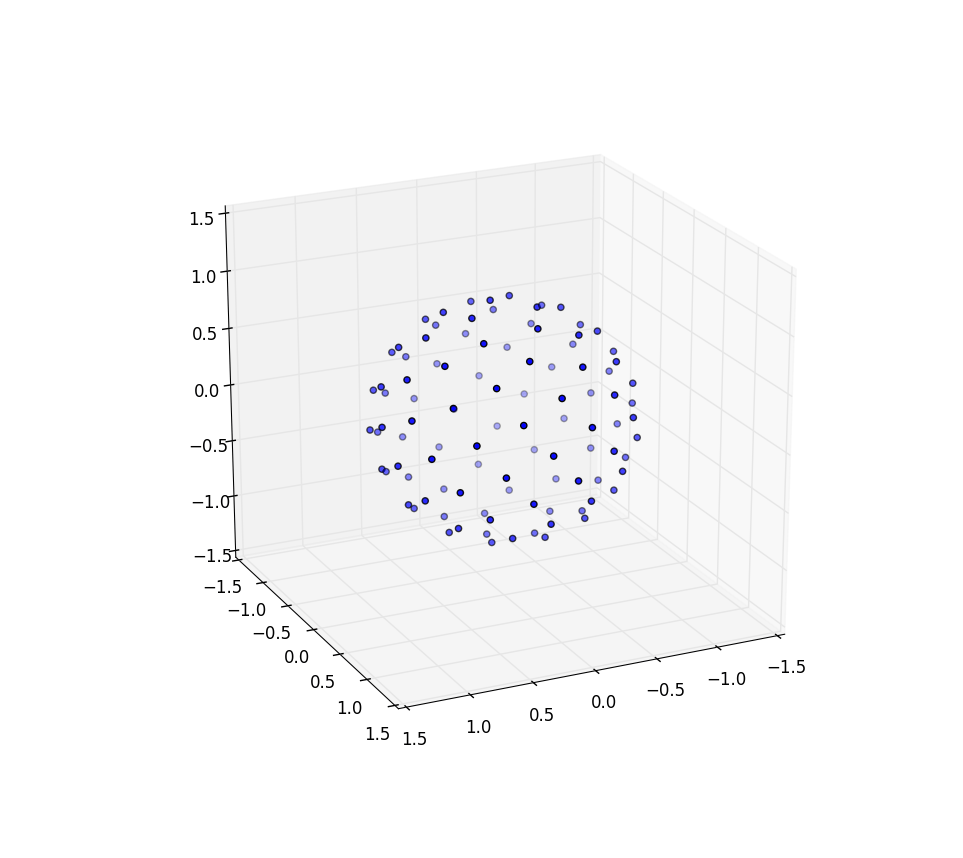 
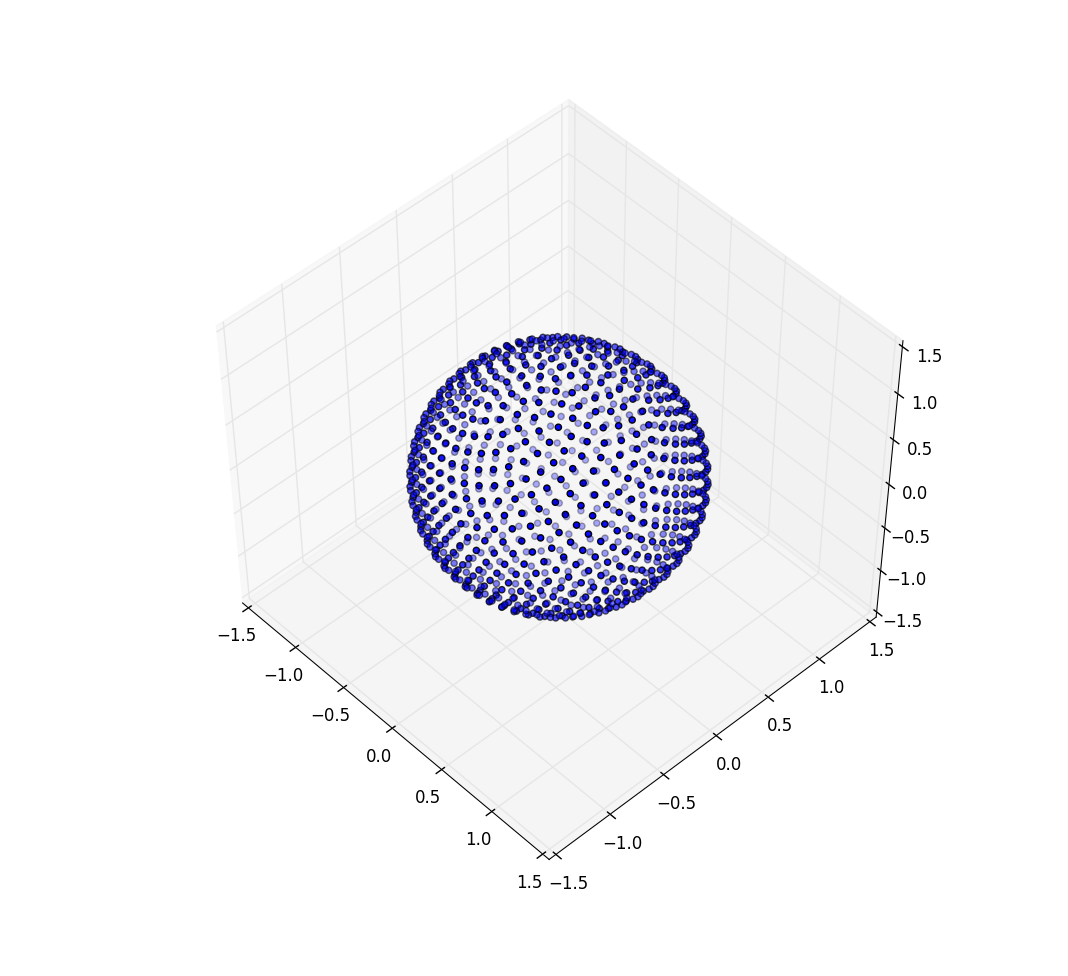
Заметки
Эти "бары" образованы рациональными приближениями к числу, а наилучшие рациональные приближения к числу получаются из его непрерывного выражения дроби,
z + 1/(n_1 + 1/(n_2 + 1/(n_3 + ...)))гдеzявляется целым числом иn_1, n_2, n_3, ...является конечной или бесконечной последовательностью натуральных чисел:def continued_fraction(r): while r != 0: n = floor(r) yield n r = 1/(r - n)Поскольку часть дроби
1/(...)всегда между нулем и единицей, большое целое число в непрерывной дроби учитывает особенно хорошую рациональную аппроксимацию: "один делится на что-то между 100 и 101" лучше, чем "один делится на что-то между 1 и 2". Поэтому самым иррациональным числом является тот, который1 + 1/(1 + 1/(1 + ...))и не имеет особенно хороших рациональных приближений; можно решить φ = 1 + 1 /φ, умножив на φ, чтобы получить формулу для золотого сечения.Для людей, которые не очень знакомы с NumPy - все функции "векторизованы", так что
sqrt(array)то же самое, что могут написать другие языкиmap(sqrt, array), Так что это компонент за компонентомsqrtприложение. То же самое относится и к делению на скаляр или сложению со скалярами - они применяются ко всем компонентам параллельно.Доказательство простое, если вы знаете, что это результат. Если вы спросите, какова вероятность того, что z < Z < z + dz, это то же самое, что спросить, какова вероятность того, что z < F-1(U) < z + dz, применить F ко всем трем выражениям, отметив, что это монотонно возрастающая функция, следовательно, F(z) < U < F(z + dz), разверните правую часть, чтобы найти F(z) + f(z) dz, и, поскольку U равномерна, эта вероятность равна f(z) dz, как и было обещано.
Это называется упаковочными точками на сфере, и не существует (известного) общего идеального решения. Однако есть много несовершенных решений. Три самых популярных, кажется, являются:
- Создать симуляцию. Рассматривайте каждую точку как электрон, ограниченный сферой, затем запустите симуляцию для определенного количества шагов. Отталкивание электронов естественным образом приведет систему к более устойчивому состоянию, когда точки находятся как можно дальше друг от друга.
- Отказ от гиперкуба. Этот причудливый метод на самом деле очень прост: вы равномерно выбираете точки (гораздо больше, чем
nиз них) внутри куба, окружающего сферу, затем отбросьте точки за пределами сферы. Рассматривайте оставшиеся точки как векторы и нормализуйте их. Это ваши "образцы" - выберитеnиз них используя какой-то метод (случайно, жадный и т. д.). - Спиральные приближения. Вы проводите спираль вокруг сферы и равномерно распределяете точки вокруг спирали. Из-за математики они более сложны для понимания, чем симуляция, но намного быстрее (и, вероятно, требуют меньше кода). Наиболее популярными, по-видимому, являются Saff, et al.
Здесь можно найти гораздо больше информации об этой проблеме.
То, что вы ищете, называется сферическим покрытием. Задача сферического покрытия очень сложна, и решения неизвестны, за исключением небольшого числа точек. Одно известно наверняка, что при наличии n точек на сфере всегда существуют две точки расстояния. d = (4-csc^2(\pi n/6(n-2)))^(1/2) или ближе.
Если вам нужен вероятностный метод для генерации точек, равномерно распределенных по сфере, это просто: генерировать точки в пространстве равномерно с помощью гауссовского распределения (он встроен в Java, нетрудно найти код для других языков). Так что в 3-х мерном пространстве нужно что-то вроде
Random r = new Random();
double[] p = { r.nextGaussian(), r.nextGaussian(), r.nextGaussian() };
Затем спроецируйте точку на сферу, нормализуя ее расстояние от начала координат.
double norm = Math.sqrt( (p[0])^2 + (p[1])^2 + (p[2])^2 );
double[] sphereRandomPoint = { p[0]/norm, p[1]/norm, p[2]/norm };
Гауссово распределение по n измерениям сферически симметрично, поэтому проекция на сферу равномерна.
Конечно, нет никакой гарантии, что расстояние между любыми двумя точками в наборе равномерно сгенерированных точек будет ограничено ниже, поэтому вы можете использовать отклонение для применения любых таких условий, которые у вас могут быть: вероятно, лучше всего сгенерировать всю коллекцию, а затем отклонить всю коллекцию, если это необходимо. (Или используйте "раннее отклонение", чтобы отклонить всю сгенерированную вами коллекцию; просто не сохраняйте одни точки и отбрасывайте другие.) Вы можете использовать формулу для d приведенное выше, минус некоторое ослабление, чтобы определить минимальное расстояние между точками, ниже которого вы отклоните набор точек. Вам придется рассчитать n выбрать 2 расстояния, и вероятность отклонения будет зависеть от провисания; Трудно сказать, как, поэтому запустите симуляцию, чтобы получить представление о соответствующей статистике.
Этот ответ основан на той же "теории", которая хорошо изложена в этом ответе
Я добавляю этот ответ как:
- Ни один из других вариантов не подходит для "единообразия" и требует "точного" (или явно не однозначного). (Принимая во внимание, что в первоначальном запросе получилось поведение, похожее на планету, как распределение, вы просто отклоняете из конечного списка k равномерно созданных точек случайным образом (случайным образом по индексу в k элементах назад).)
- Ближайший другой подтолкнул вас к определению "N" по "угловой оси", а не только по "одному значению N" по обеим значениям угловой оси (что при малых значениях N очень сложно узнать, что может, или может не иметь значения (например, вы хотите 5 баллов - получайте удовольствие))
- Кроме того, очень трудно "уловить", как провести различие между другими опциями без каких-либо изображений, поэтому вот как выглядит эта опция (ниже) и готовая к запуску реализация, которая сопровождает его.
с N на 20:
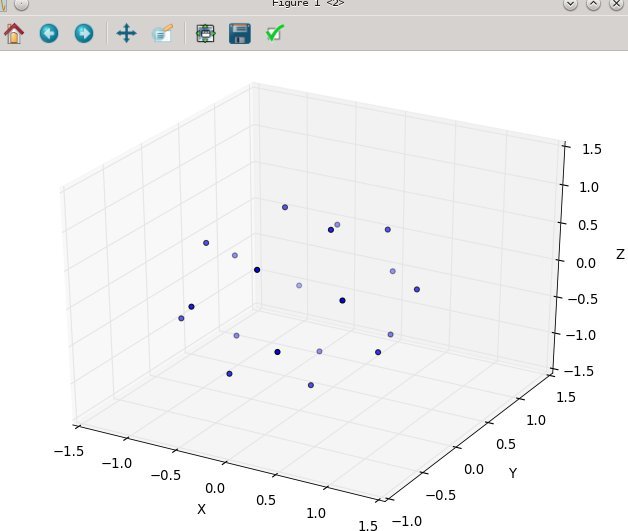
а затем N на 80:
вот готовый к запуску код на python3, где эмуляция - это тот же источник: " http://web.archive.org/web/20120421191837/http://www.cgafaq.info/wiki/Evenly_distributed_points_on_sphere ", найденный другими, (График, который я включил, который запускается при запуске как "основной", взят с: http://www.scipy.org/Cookbook/Matplotlib/mplot3D)
from math import cos, sin, pi, sqrt
def GetPointsEquiAngularlyDistancedOnSphere(numberOfPoints=45):
""" each point you get will be of form 'x, y, z'; in cartesian coordinates
eg. the 'l2 distance' from the origion [0., 0., 0.] for each point will be 1.0
------------
converted from: http://web.archive.org/web/20120421191837/http://www.cgafaq.info/wiki/Evenly_distributed_points_on_sphere )
"""
dlong = pi*(3.0-sqrt(5.0)) # ~2.39996323
dz = 2.0/numberOfPoints
long = 0.0
z = 1.0 - dz/2.0
ptsOnSphere =[]
for k in range( 0, numberOfPoints):
r = sqrt(1.0-z*z)
ptNew = (cos(long)*r, sin(long)*r, z)
ptsOnSphere.append( ptNew )
z = z - dz
long = long + dlong
return ptsOnSphere
if __name__ == '__main__':
ptsOnSphere = GetPointsEquiAngularlyDistancedOnSphere( 80)
#toggle True/False to print them
if( True ):
for pt in ptsOnSphere: print( pt)
#toggle True/False to plot them
if(True):
from numpy import *
import pylab as p
import mpl_toolkits.mplot3d.axes3d as p3
fig=p.figure()
ax = p3.Axes3D(fig)
x_s=[];y_s=[]; z_s=[]
for pt in ptsOnSphere:
x_s.append( pt[0]); y_s.append( pt[1]); z_s.append( pt[2])
ax.scatter3D( array( x_s), array( y_s), array( z_s) )
ax.set_xlabel('X'); ax.set_ylabel('Y'); ax.set_zlabel('Z')
p.show()
#end
проверено на низких счетах (N в 2, 5, 7, 13 и т. д.) и, кажется, работает "хорошо"
Пытаться:
function sphere ( N:float,k:int):Vector3 {
var inc = Mathf.PI * (3 - Mathf.Sqrt(5));
var off = 2 / N;
var y = k * off - 1 + (off / 2);
var r = Mathf.Sqrt(1 - y*y);
var phi = k * inc;
return Vector3((Mathf.Cos(phi)*r), y, Mathf.Sin(phi)*r);
};
Вышеприведенная функция должна выполняться в цикле с общим количеством N циклов и текущей итерацией k циклов.
Это основано на структуре семян подсолнечника, за исключением того, что семена подсолнечника изогнуты вокруг в половину купола, и снова в сферу.
Вот изображение, за исключением того, что я поместил камеру наполовину внутри сферы, чтобы она выглядела 2d вместо 3d, потому что камера находится на одинаковом расстоянии от всех точек. http://3.bp.blogspot.com/-9lbPHLccQHA/USXf88_bvVI/AAAAAAAAADY/j7qhQsSZsA8/s640/sphere.jpg
Healpix решает тесно связанную проблему (пикселирование сферы равными по площади пикселями):
http://healpix.sourceforge.net/
Возможно, это излишне, но, возможно, после просмотра вы поймете, что некоторые из его приятных свойств вам интересны. Это гораздо больше, чем просто функция, которая выводит облако точек.
Я приземлился здесь, пытаясь найти его снова; название "healpix" не совсем напоминает сферы...
редактировать: Это не отвечает на вопрос, который ОП хотел задать, оставляя его здесь на случай, если люди найдут его полезным.
Мы используем правило вероятности умножения в сочетании с бесконечно малыми числами. В результате получается 2 строки кода для достижения желаемого результата:
longitude: φ = uniform([0,2pi))
azimuth: θ = -arcsin(1 - 2*uniform([0,1]))
(определяется в следующей системе координат:)
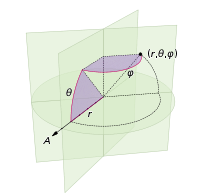
Ваш язык обычно имеет единый примитив случайных чисел. Например, в Python вы можете использовать random.random() вернуть число в диапазоне [0,1), Вы можете умножить это число на k, чтобы получить случайное число в диапазоне [0,k), Таким образом, в Python, uniform([0,2pi)) будет означать random.random()*2*math.pi,
доказательство
Теперь мы не можем назначить θ равномерно, иначе мы бы слиплись на полюсах. Мы хотим назначить вероятности, пропорциональные площади поверхности сферического клина (θ на этой диаграмме фактически φ):
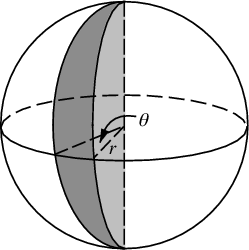
Угловое смещение dφ на экваторе приведет к смещению dφ*r. Каким будет это смещение при произвольном азимуте? Ну, радиус от оси Z r*sin(θ)поэтому длина этой "широты", пересекающей клин, равна dφ * r*sin(θ), Таким образом, мы рассчитываем совокупное распределение площади для выборки из нее путем интегрирования площади среза от южного полюса до северного полюса.
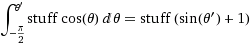(где вещи =dφ*r)
Теперь мы попытаемся получить инверсию CDF для выборки из него: http://en.wikipedia.org/wiki/Inverse_transform_sampling
Сначала мы нормализуем, разделив наш почти-CDF на его максимальное значение. Это имеет побочный эффект отмены dφ и r.
azimuthalCDF: cumProb = (sin(θ)+1)/2 from -pi/2 to pi/2
inverseCDF: θ = -sin^(-1)(1 - 2*cumProb)
Таким образом:
let x by a random float in range [0,1]
θ = -arcsin(1-2*x)
С небольшим количеством точек вы можете запустить симуляцию:
from random import random,randint
r = 10
n = 20
best_closest_d = 0
best_points = []
points = [(r,0,0) for i in range(n)]
for simulation in range(10000):
x = random()*r
y = random()*r
z = r-(x**2+y**2)**0.5
if randint(0,1):
x = -x
if randint(0,1):
y = -y
if randint(0,1):
z = -z
closest_dist = (2*r)**2
closest_index = None
for i in range(n):
for j in range(n):
if i==j:
continue
p1,p2 = points[i],points[j]
x1,y1,z1 = p1
x2,y2,z2 = p2
d = (x1-x2)**2+(y1-y2)**2+(z1-z2)**2
if d < closest_dist:
closest_dist = d
closest_index = i
if simulation % 100 == 0:
print simulation,closest_dist
if closest_dist > best_closest_d:
best_closest_d = closest_dist
best_points = points[:]
points[closest_index]=(x,y,z)
print best_points
>>> best_points
[(9.921692138442777, -9.930808529773849, 4.037839326088124),
(5.141893371460546, 1.7274947332807744, -4.575674650522637),
(-4.917695758662436, -1.090127967097737, -4.9629263893193745),
(3.6164803265540666, 7.004158551438312, -2.1172868271109184),
(-9.550655088997003, -9.580386054762917, 3.5277052594769422),
(-0.062238110294250415, 6.803105171979587, 3.1966101417463655),
(-9.600996012203195, 9.488067284474834, -3.498242301168819),
(-8.601522086624803, 4.519484132245867, -0.2834204048792728),
(-1.1198210500791472, -2.2916581379035694, 7.44937337008726),
(7.981831370440529, 8.539378431788634, 1.6889099589074377),
(0.513546008372332, -2.974333486904779, -6.981657873262494),
(-4.13615438946178, -6.707488383678717, 2.1197605651446807),
(2.2859494919024326, -8.14336582650039, 1.5418694699275672),
(-7.241410895247996, 9.907335206038226, 2.271647103735541),
(-9.433349952523232, -7.999106443463781, -2.3682575660694347),
(3.704772125650199, 1.0526567864085812, 6.148581714099761),
(-3.5710511242327048, 5.512552040316693, -3.4318468250897647),
(-7.483466337225052, -1.506434920354559, 2.36641535124918),
(7.73363824231576, -8.460241422163824, -1.4623228616326003),
(10, 0, 0)]
Основываясь на ответе fnord, вот версия Unity3D с добавленными диапазонами:
Код:
// golden angle in radians
static float Phi = Mathf.PI * ( 3f - Mathf.Sqrt( 5f ) );
static float Pi2 = Mathf.PI * 2;
public static Vector3 Point( float radius , int index , int total , float min = 0f, float max = 1f , float angleStartDeg = 0f, float angleRangeDeg = 360 )
{
// y goes from min (-) to max (+)
var y = ( ( index / ( total - 1f ) ) * ( max - min ) + min ) * 2f - 1f;
// golden angle increment
var theta = Phi * index ;
if( angleStartDeg != 0 || angleRangeDeg != 360 )
{
theta = ( theta % ( Pi2 ) ) ;
theta = theta < 0 ? theta + Pi2 : theta ;
var a1 = angleStartDeg * Mathf.Deg2Rad;
var a2 = angleRangeDeg * Mathf.Deg2Rad;
theta = theta * a2 / Pi2 + a1;
}
// https://stackoverflow.com/a/26127012/2496170
// radius at y
var rY = Mathf.Sqrt( 1 - y * y );
var x = Mathf.Cos( theta ) * rY;
var z = Mathf.Sin( theta ) * rY;
return new Vector3( x, y, z ) * radius;
}
Суть: https://gist.github.com/nukadelic/7449f0872f708065bc1afeb19df666f7/edit
Предварительный просмотр:
Джонатан Коган предложил новый метод (2016, pdf) для создания решения, которое решает эту проблему полуточно, одновременно не ставя под угрозу скорость:
import math
def spherical_coordinate(x, y):
return [
math.cos(x) * math.cos(y),
math.sin(x) * math.cos(y),
math.sin(y)
]
def NX(n, x):
pts = []
start = (-1. + 1. / (n - 1.))
increment = (2. - 2. / (n - 1.)) / (n - 1.)
for j in xrange(0, n):
s = start + j * increment
pts.append(
spherical_cordinate(
s * x, math.pi / 2. *
math.copysign(1, s) *
(1. - math.sqrt(1. - abs(s)))
)
)
return pts
def generate_points(n):
return NX(n, 0.1 + 1.2 * n)
Быстрый и хороший метод распространения — равноудаленная спираль Архимеда: https://agupubs.onlinelibrary.wiley.com/doi/pdf/10.1029/2007GC001581 . Ключевым ингредиентом является второй неполный эллиптический интеграл ( https://docs.scipy.org/doc/scipy/reference/generated/scipy.special.elipeinc.html#scipy.special.elipeinc ). Моделирование отталкивания дает лучшие результаты, но имеет высокую сложность. О(Н^2).
Возьмите два крупнейших фактора вашего N, если N==20 тогда два крупнейших фактора {5,4}или, в более общем плане {a,b}, подсчитывать
dlat = 180/(a+1)
dlong = 360/(b+1})
Поставь свою первую точку на {90-dlat/2,(dlong/2)-180}, ваш второй в {90-dlat/2,(3*dlong/2)-180}Ваш третий в {90-dlat/2,(5*dlong/2)-180}до тех пор, пока вы не споткнетесь вокруг света один раз, когда {75,150} когда вы идете рядом с {90-3*dlat/2,(dlong/2)-180},
Очевидно, я работаю над этим в градусах на поверхности сферической земли, с обычными соглашениями для перевода +/- в N/S или E/W. И, очевидно, это дает вам совершенно неслучайное распределение, но оно равномерно и точки не сгруппированы вместе.
Чтобы добавить некоторую степень случайности, вы можете сгенерировать 2 нормально распределенных (со средним 0 и стандартным отклонением {dlat/3, dlong/3} соответственно) и добавить их к вашим равномерно распределенным точкам.
ИЛИ... чтобы разместить 20 точек, вычислите центры граней икосаэдра. Для 12 точек найдите вершины икосаэдра. Для 30 точек - средняя точка краев икосаэдра. вы можете сделать то же самое с тетраэдром, кубом, додекаэдром и октаэдром: один набор точек находится на вершинах, другой - в центре грани, а другой - в центре ребер. Однако их нельзя смешивать.
@robert king Это действительно хорошее решение, но в нем есть несколько неряшливых ошибок. Я знаю, что это мне очень помогло, так что не говоря уже о неряшливости.:) Вот и исправленная версия....
from math import pi, asin, sin, degrees
halfpi, twopi = .5 * pi, 2 * pi
sphere_area = lambda R=1.0: 4 * pi * R ** 2
lat_dist = lambda lat, R=1.0: R*(1-sin(lat))
#A = 2*pi*R^2(1-sin(lat))
def sphere_latarea(lat, R=1.0):
if -halfpi > lat or lat > halfpi:
raise ValueError("lat must be between -halfpi and halfpi")
return 2 * pi * R ** 2 * (1-sin(lat))
sphere_lonarea = lambda lon, R=1.0: \
4 * pi * R ** 2 * lon / twopi
#A = 2*pi*R^2 |sin(lat1)-sin(lat2)| |lon1-lon2|/360
# = (pi/180)R^2 |sin(lat1)-sin(lat2)| |lon1-lon2|
sphere_rectarea = lambda lat0, lat1, lon0, lon1, R=1.0: \
(sphere_latarea(lat0, R)-sphere_latarea(lat1, R)) * (lon1-lon0) / twopi
def test_sphere(n_lats=10, n_lons=19, radius=540.0):
total_area = 0.0
for i_lons in range(n_lons):
lon0 = twopi * float(i_lons) / n_lons
lon1 = twopi * float(i_lons+1) / n_lons
for i_lats in range(n_lats):
lat0 = asin(2 * float(i_lats) / n_lats - 1)
lat1 = asin(2 * float(i_lats+1)/n_lats - 1)
area = sphere_rectarea(lat0, lat1, lon0, lon1, radius)
print("{:} {:}: {:9.4f} to {:9.4f}, {:9.4f} to {:9.4f} => area {:10.4f}"
.format(i_lats, i_lons
, degrees(lat0), degrees(lat1)
, degrees(lon0), degrees(lon1)
, area))
total_area += area
print("total_area = {:10.4f} (difference of {:10.4f})"
.format(total_area, abs(total_area) - sphere_area(radius)))
test_sphere()
# create uniform spiral grid
numOfPoints = varargin[0]
vxyz = zeros((numOfPoints,3),dtype=float)
sq0 = 0.00033333333**2
sq2 = 0.9999998**2
sumsq = 2*sq0 + sq2
vxyz[numOfPoints -1] = array([(sqrt(sq0/sumsq)),
(sqrt(sq0/sumsq)),
(-sqrt(sq2/sumsq))])
vxyz[0] = -vxyz[numOfPoints -1]
phi2 = sqrt(5)*0.5 + 2.5
rootCnt = sqrt(numOfPoints)
prevLongitude = 0
for index in arange(1, (numOfPoints -1), 1, dtype=float):
zInc = (2*index)/(numOfPoints) -1
radius = sqrt(1-zInc**2)
longitude = phi2/(rootCnt*radius)
longitude = longitude + prevLongitude
while (longitude > 2*pi):
longitude = longitude - 2*pi
prevLongitude = longitude
if (longitude > pi):
longitude = longitude - 2*pi
latitude = arccos(zInc) - pi/2
vxyz[index] = array([ (cos(latitude) * cos(longitude)) ,
(cos(latitude) * sin(longitude)),
sin(latitude)])
Это работает, и это смертельно просто. Столько очков, сколько вы хотите:
private function moveTweets():void {
var newScale:Number=Scale(meshes.length,50,500,6,2);
trace("new scale:"+newScale);
var l:Number=this.meshes.length;
var tweetMeshInstance:TweetMesh;
var destx:Number;
var desty:Number;
var destz:Number;
for (var i:Number=0;i<this.meshes.length;i++){
tweetMeshInstance=meshes[i];
var phi:Number = Math.acos( -1 + ( 2 * i ) / l );
var theta:Number = Math.sqrt( l * Math.PI ) * phi;
tweetMeshInstance.origX = (sphereRadius+5) * Math.cos( theta ) * Math.sin( phi );
tweetMeshInstance.origY= (sphereRadius+5) * Math.sin( theta ) * Math.sin( phi );
tweetMeshInstance.origZ = (sphereRadius+5) * Math.cos( phi );
destx=sphereRadius * Math.cos( theta ) * Math.sin( phi );
desty=sphereRadius * Math.sin( theta ) * Math.sin( phi );
destz=sphereRadius * Math.cos( phi );
tweetMeshInstance.lookAt(new Vector3D());
TweenMax.to(tweetMeshInstance, 1, {scaleX:newScale,scaleY:newScale,x:destx,y:desty,z:destz,onUpdate:onLookAtTween, onUpdateParams:[tweetMeshInstance]});
}
}
private function onLookAtTween(theMesh:TweetMesh):void {
theMesh.lookAt(new Vector3D());
}