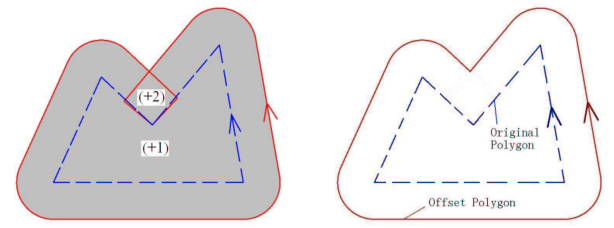
Алгоритм накачивания / выкачивания (смещения, буферизации) полигонов
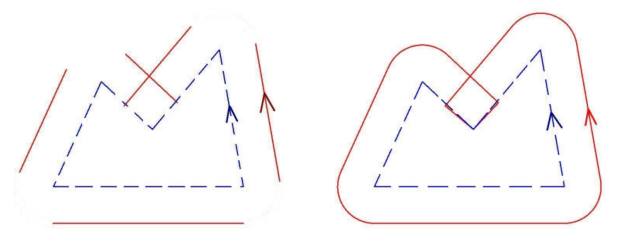
Как бы я "надул" многоугольник? То есть я хочу сделать что-то похожее на это:
Требование состоит в том, что ребра / точки нового (надутого) многоугольника находятся на одном и том же постоянном расстоянии от старого (исходного) многоугольника (на примере изображения это не так, поскольку тогда придется использовать дуги для завышенных вершин, но давайте забудь об этом сейчас;)).
Математический термин для того, что я ищу, на самом деле является смещением полигонов внутрь / наружу. +1 к балтинту за указание на это. Альтернативное наименование - буферизация полигонов.
Результаты моего поиска:
Вот несколько ссылок:
15 ответов
Я подумал, что могу кратко упомянуть мою собственную библиотеку отсечения и смещения полигонов - Clipper.
Хотя Clipper в первую очередь предназначен для операций срезания полигонов, он также выполняет смещение полигонов. Библиотека с открытым исходным кодом написана на Delphi, C++ и C#. Он имеет очень свободную лицензию Boost, позволяющую бесплатно использовать ее как в бесплатных, так и в коммерческих приложениях.
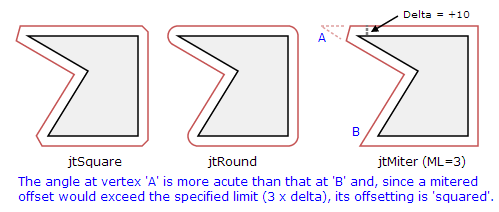
Смещение полигонов может быть выполнено с использованием одного из трех стилей смещения - квадрат, округление и сглаживание.
Нужный многоугольник в вычислительной геометрии называется смещенным внутрь / наружу многоугольником и тесно связан с прямым скелетом.
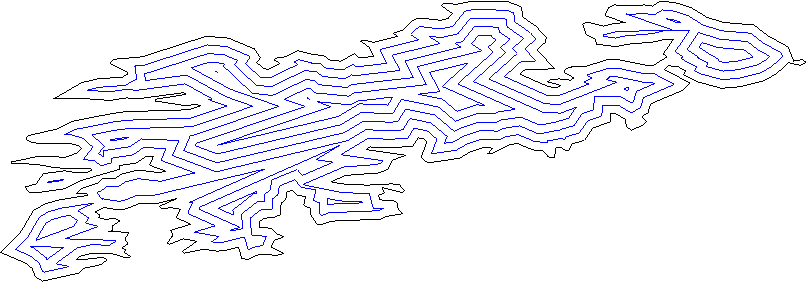
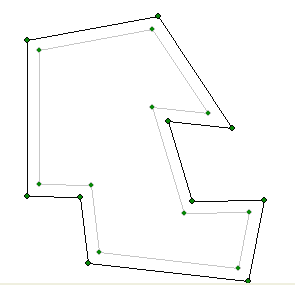
Это несколько смещенных многоугольников для сложного многоугольника:
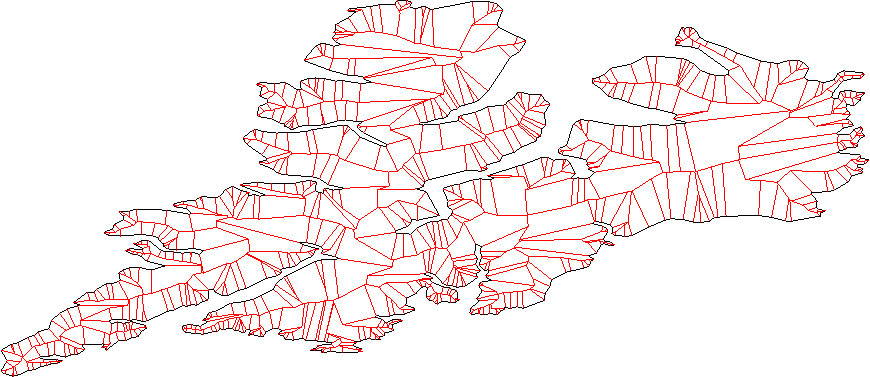
И это прямой скелет для другого многоугольника:
Как указывалось и в других комментариях, в зависимости от того, насколько далеко вы планируете "надувать / выкачивать" свой полигон, вы можете получить разные возможности подключения для вывода.
С вычислительной точки зрения: если у вас есть прямой скелет, вы сможете относительно легко построить смещенные полигоны. Библиотека CGAL с открытым исходным кодом и (бесплатная для некоммерческих) имеет пакет, реализующий эти структуры. Посмотрите этот пример кода, чтобы вычислить смещенные полигоны, используя CGAL.
Руководство по пакету должно дать вам хорошее начальное представление о том, как построить эти структуры, даже если вы не собираетесь использовать CGAL, и содержит ссылки на статьи с математическими определениями и свойствами:
Руководство CGAL: 2D прямолинейное смещение скелета и многоугольника
Я никогда не использовал Clipper (разработанный Ангусом Джонсоном), но для таких вещей я обычно использую JTS. В демонстрационных целях я создал этот jsFiddle, который использует JSTS (порт JavaScript JTS). Вам просто нужно преобразовать нужные вам координаты в координаты JSTS:
function vectorCoordinates2JTS (polygon) {
var coordinates = [];
for (var i = 0; i < polygon.length; i++) {
coordinates.push(new jsts.geom.Coordinate(polygon[i].x, polygon[i].y));
}
return coordinates;
}
Результат примерно такой:
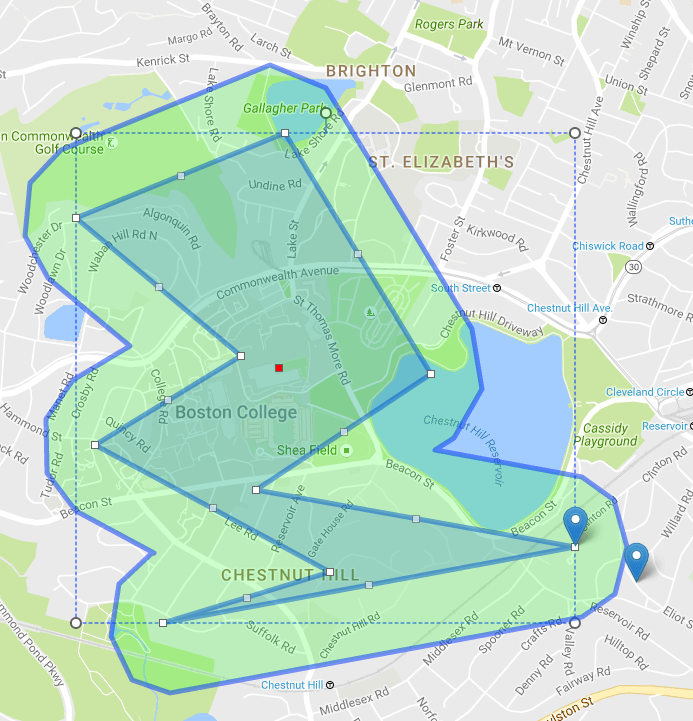
Дополнительная информация: Я обычно использую этот тип надувания / выкачивания (немного измененный для моих целей) для установки границ с радиусом на многоугольниках, которые нарисованы на карте (с картами Leaflet или Google). Вы просто конвертируете (lat,lng) пары в координаты JSTS, а все остальное тоже самое. Пример:
Похоже, что вы хотите, это:
- Начиная с вершины, лицом против часовой стрелки вдоль смежного края.
- Замените ребро новым параллельным ребром, расположенным на расстоянии
d"слева" от старого. - Повторите для всех краев.
- Найдите пересечения новых ребер, чтобы получить новые вершины.
- Определите, стал ли вы скрещенным полиномом, и решите, что с этим делать. Вероятно, добавьте новую вершину в точке пересечения и избавьтесь от некоторых старых. Я не уверен, есть ли лучший способ обнаружить это, чем просто сравнить каждую пару несмежных ребер, чтобы увидеть, находится ли их пересечение между обеими парами вершин.
Полученный многоугольник лежит на необходимом расстоянии от старого многоугольника "достаточно далеко" от вершин. Рядом с вершиной множество точек на расстоянии d из старого многоугольника, как вы говорите, не является многоугольником, поэтому указанное требование не может быть выполнено.
Я не знаю, есть ли у этого алгоритма имя, пример кода в Интернете или злобная оптимизация, но я думаю, что он описывает то, что вы хотите.
В мире ГИС для этой задачи используется отрицательная буферизация: http://www-users.cs.umn.edu/~npramod/enc_pdf.pdf
Библиотека JTS должна сделать это за вас. См. Документацию по операции с буфером: http://tsusiatsoftware.net/jts/javadoc/com/vividsolutions/jts/operation/buffer/package-summary.html
Для приблизительного обзора см. Также Руководство разработчика: http://www.vividsolutions.com/jts/bin/JTS%20Developer%20Guide.pdf
Вот альтернативное решение, посмотрите, нравится ли вам это больше.
Сделайте триангуляцию, это не должно быть Делоне - подойдет любая триангуляция.
Раздуйте каждый треугольник - это должно быть тривиально. если вы сохраняете треугольник в направлении против часовой стрелки, просто переместите линии вправо и сделайте пересечение.
Объедините их, используя модифицированный алгоритм отсечения Вейлера-Атертона
Большое спасибо Ангусу Джонсону за его библиотеку клиперов. Есть хорошие примеры кода для выполнения отсечения на домашней странице отсечения по адресу http://www.angusj.com/delphi/clipper.php но я не видел пример смещения полигонов. Поэтому я подумал, что, может быть, кому-то это пригодится, если я выложу свой код:
public static List<Point> GetOffsetPolygon(List<Point> originalPath, double offset)
{
List<Point> resultOffsetPath = new List<Point>();
List<ClipperLib.IntPoint> polygon = new List<ClipperLib.IntPoint>();
foreach (var point in originalPath)
{
polygon.Add(new ClipperLib.IntPoint(point.X, point.Y));
}
ClipperLib.ClipperOffset co = new ClipperLib.ClipperOffset();
co.AddPath(polygon, ClipperLib.JoinType.jtRound, ClipperLib.EndType.etClosedPolygon);
List<List<ClipperLib.IntPoint>> solution = new List<List<ClipperLib.IntPoint>>();
co.Execute(ref solution, offset);
foreach (var offsetPath in solution)
{
foreach (var offsetPathPoint in offsetPath)
{
resultOffsetPath.Add(new Point(Convert.ToInt32(offsetPathPoint.X), Convert.ToInt32(offsetPathPoint.Y)));
}
}
return resultOffsetPath;
}
Каждая линия должна разбивать плоскость на "внутрь" и "контур"; Вы можете узнать это, используя обычный метод внутреннего продукта.
Переместите все линии наружу на некоторое расстояние.
Рассмотрим всю пару соседних линий (линии, а не отрезок), найдите пересечение. Это новая вершина.
Очистите новую вершину, удалив все пересекающиеся части. - у нас есть несколько случаев здесь
(а) Случай 1:
0--7 4--3
| | | |
| 6--5 |
| |
1--------2
если вы потратите его на одного, вы получите это:
0----a----3
| | |
| | |
| b |
| |
| |
1---------2
7 и 4 перекрываются.. если вы видите это, вы удаляете эту точку и все точки между ними.
(б) случай 2
0--7 4--3
| | | |
| 6--5 |
| |
1--------2
если вы потратите его на два, вы получите это:
0----47----3
| || |
| || |
| || |
| 56 |
| |
| |
| |
1----------2
Чтобы решить эту проблему, для каждого сегмента линии необходимо проверить, не перекрываются ли они с последними сегментами.
(в) дело 3
4--3
0--X9 | |
| 78 | |
| 6--5 |
| |
1--------2
Расход на 1. Это более общий случай для случая 1.
(d) дело 4
так же, как case3, но расход на два.
На самом деле, если вы можете обработать случай 4. Все другие случаи - это просто особый случай с некоторым перекрытием линий или вершин.
Для случая 4 вы сохраняете стек вершин. Вы нажимаете, когда обнаруживаете, что линии перекрываются с последней, и выталкиваете его, когда получаете последнюю строку. - так же, как то, что вы делаете в выпуклой оболочке.
Еще одним вариантом является использование boost:: polygon - документации немного не хватает, но вы должны обнаружить, что методы resize а также bloat, а также перегружен += оператор, который фактически реализует буферизацию. Так, например, увеличение размера многоугольника (или набора многоугольников) на некоторое значение может быть простым:
poly += 2; // buffer polygon by 2
Я использую простую геометрию: векторы и / или тригонометрию.
На каждом углу найдите средний вектор и средний угол. Средний вектор - это среднее арифметическое двух единичных векторов, определенных краями угла. Средний угол - это половина угла, определяемого краями.
Если вам нужно расширить (или сжать) многоугольник на величину d от каждого края; вы должны выйти (внутрь) на величину d/sin(midAngle), чтобы получить новую угловую точку.
Повторите это для всех углов
*** Будьте осторожны со своим направлением. Выполните CounterClockWise Test, используя три точки, определяющие угол; чтобы узнать, какой выход - вовнутрь.
Основываясь на совете от @JoshO'Brian, кажется, rGeos пакет в R язык реализует этот алгоритм. Увидеть rGeos::gBuffer,
Для раздувания многоугольника можно реализовать алгоритм из статьи "Смещение многоугольника путем вычисления чисел намотки" .
Шаги алгоритма следующие:
- Постройте внешнюю кривую смещения, взяв каждое ребро из входного многоугольника и сдвинув его наружу, затем соединив смещенные ребра с круговыми дугами в выпуклых вершинах входного многоугольника и двумя отрезками прямых в вогнутых вершинах входного многоугольника.
Пример. Здесь входной многоугольник заштрихован синим, а красным слева — сдвинутые ребра, справа — после соединения их в непрерывную самопересекающуюся кривую:
- Кривая делит плоскость на ряд связных компонентов, и нужно вычислить число витков в каждом из них, затем взять границу всех связных компонентов с положительными номерами витков:
Статья доказывает, что алгоритм очень быстр по сравнению с конкурентами и в то же время надежен.
Чтобы избежать вычисления числа витков, можно передать самопересекающуюся кривую смещения в тесселятор OpenGL Utility library (GLU) и активировать настройкиGLU_TESS_BOUNDARY_ONLY=GL_TRUE(чтобы пропустить триангуляцию) иGLU_TESS_WINDING_RULE=GLU_TESS_WINDING_POSITIVE(для вывода границы компонентов с положительным номером обмотки).
Спасибо за помощь в этой теме, вот код на C++, если кому интересно. Протестировал, работает. Если вы зададите offset = -1,5, полигон уменьшится.
typedef struct {
double x;
double y;
} Point2D;
double Hypot(double x, double y)
{
return std::sqrt(x * x + y * y);
}
Point2D NormalizeVector(const Point2D& p)
{
double h = Hypot(p.x, p.y);
if (h < 0.0001)
return Point2D({ 0.0, 0.0 });
double inverseHypot = 1 / h;
return Point2D({ (double)p.x * inverseHypot, (double)p.y * inverseHypot });
}
void offsetPolygon(std::vector<Point2D>& polyCoords, std::vector<Point2D>& newPolyCoords, double offset, int outer_ccw)
{
if (offset == 0.0 || polyCoords.size() < 3)
return;
Point2D vnn, vpn, bisn;
double vnX, vnY, vpX, vpY;
double nnnX, nnnY;
double npnX, npnY;
double bisX, bisY, bisLen;
unsigned int nVerts = polyCoords.size() - 1;
for (unsigned int curr = 0; curr < polyCoords.size(); curr++)
{
int prev = (curr + nVerts - 1) % nVerts;
int next = (curr + 1) % nVerts;
vnX = polyCoords[next].x - polyCoords[curr].x;
vnY = polyCoords[next].y - polyCoords[curr].y;
vnn = NormalizeVector({ vnX, vnY });
nnnX = vnn.y;
nnnY = -vnn.x;
vpX = polyCoords[curr].x - polyCoords[prev].x;
vpY = polyCoords[curr].y - polyCoords[prev].y;
vpn = NormalizeVector({ vpX, vpY });
npnX = vpn.y * outer_ccw;
npnY = -vpn.x * outer_ccw;
bisX = (nnnX + npnX) * outer_ccw;
bisY = (nnnY + npnY) * outer_ccw;
bisn = NormalizeVector({ bisX, bisY });
bisLen = offset / std::sqrt((1 + nnnX * npnX + nnnY * npnY) / 2);
newPolyCoords.push_back({ polyCoords[curr].x + bisLen * bisn.x, polyCoords[curr].y + bisLen * bisn.y });
}
}
Есть несколько библиотек, которые можно использовать (также можно использовать для наборов трехмерных данных).
- https://github.com/otherlab/openmesh
- https://github.com/alecjacobson/nested_cages
- http://homepage.tudelft.nl/h05k3/Projects/MeshThickeningProj.htm
Можно также найти соответствующие публикации для этих библиотек, чтобы понять алгоритмы более подробно.
Последний имеет наименьшие зависимости, является автономным и может читать в файлах.obj.
С наилучшими пожеланиями, Стефан
Это реализация C# алгоритма, описанного здесь . Он также использует математическую библиотеку Unity и пакет сбора.
public static NativeArray<float2> ExpandPoly(NativeArray<float2> oldPoints, float offset, int outer_ccw = 1)
{
int num_points = oldPoints.Length;
NativeArray<float2> newPoints = new NativeArray<float2>(num_points, Allocator.Temp);
for (int curr = 0; curr < num_points; curr++)
{
int prev = (curr + num_points - 1) % num_points;
int next = (curr + 1) % num_points;
float2 vn = oldPoints[next] - oldPoints[curr];
float2 vnn = math.normalize(vn);
float nnnX = vnn.y;
float nnnY = -vnn.x;
float2 vp = oldPoints[curr] - oldPoints[prev];
float2 vpn = math.normalize(vp);
float npnX = vpn.y * outer_ccw;
float npnY = -vpn.x * outer_ccw;
float bisX = (nnnX + npnX) * outer_ccw;
float bisY = (nnnY + npnY) * outer_ccw;
float2 bisn = math.normalize(new float2(bisX, bisY));
float bislen = offset / math.sqrt((1 + nnnX * npnX + nnnY * npnY) / 2);
newPoints[curr] = new float2(oldPoints[curr].x + bislen * bisn.x, oldPoints[curr].y + bislen * bisn.y);
}
return newPoints;
}