Линейная регрессия с использованием lm() - удивлен результатом

Question

Я использовал линейную регрессию на данных, которые у меня есть, используя lm функция. Все работает (без сообщения об ошибке), но я как-то удивлен результатом: у меня сложилось впечатление, что R "пропускает" группу точек, то есть точка пересечения и наклон не подходят лучше всего. Например, я имею в виду группу точек с координатами x=15-25,y=0-20.

Мои вопросы:

• есть ли функция для сравнения соответствия с "ожидаемыми" коэффициентами и "лм-рассчитанными" коэффициентами?
• я сделал глупую ошибку при кодировании, ведя lm сделать это?

После некоторых ответов: дополнительная информация о х и у

x и y являются визуальными оценками симптомов заболевания. У них обоих одинаковая неопределенность.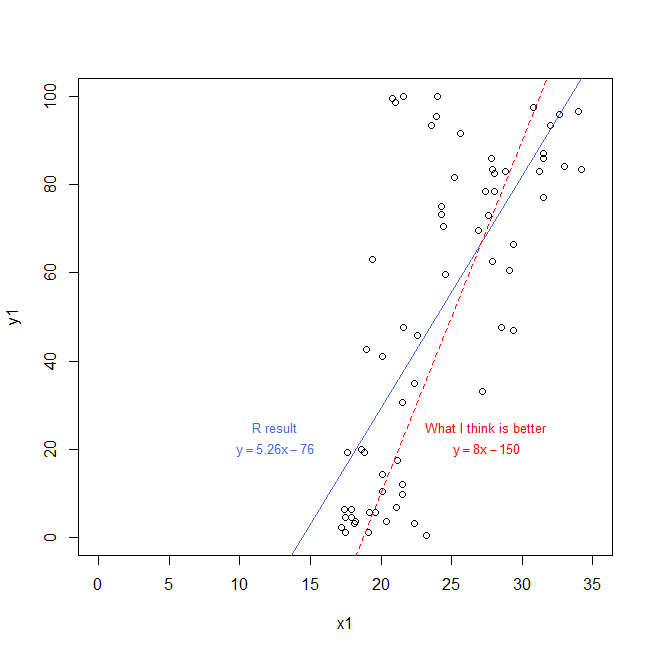

Данные и код здесь:

x1=c(24.0,23.9,23.6,21.6,21.0,20.8,22.4,22.6,
     21.6,21.2,19.0,19.4,21.1,21.5,21.5,20.1,20.1,
     20.1,17.2,18.6,21.5,18.2,23.2,20.4,19.2,22.4,
     18.8,17.9,19.1,17.9,19.6,18.1,17.6,17.4,17.5,
     17.5,25.2,24.4,25.6,24.3,24.6,24.3,29.4,29.4,
     29.1,28.5,27.2,27.9,31.5,31.5,31.5,27.8,31.2,
     27.4,28.8,27.9,27.6,26.9,28.0,28.0,33.0,32.0,
     34.2,34.0,32.6,30.8)

y1=c(100.0,95.5,93.5,100.0,98.5,99.5,34.8,
     45.8,47.5,17.4,42.6,63.0,6.9,12.1,30.5,
     10.5,14.3,41.1, 2.2,20.0,9.8,3.5,0.5,3.5,5.7,
     3.1,19.2,6.4, 1.2, 4.5, 5.7, 3.1,19.2, 6.4,
     1.2,4.5,81.5,70.5,91.5,75.0,59.5,73.3,66.5,
     47.0,60.5,47.5,33.0,62.5,87.0,86.0,77.0,
     86.0,83.0,78.5,83.0,83.5,73.0,69.5,82.5,78.5,
     84.0,93.5,83.5,96.5,96.0,97.5)   



## x11()
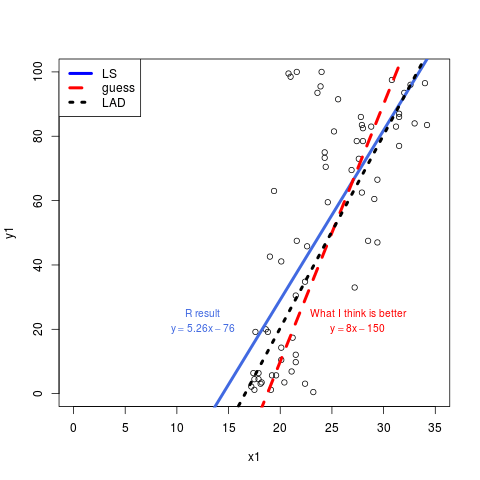
plot(x1,y1,xlim=c(0,35),ylim=c(0,100))

# linear regression
reg_lin=lm(y1 ~ x1)
abline(reg_lin,lty="solid", col="royalblue")
text(12.5,25,labels="R result",col="royalblue", cex=0.85)
text(12.5,20,labels=bquote(y== .(5.26)*x - .(76)),col="royalblue", cex=0.85)

# result I would have imagined
abline(a=-150,b=8,lty="dashed", col="red")
text(27.5,25,labels="What I think is better",col="red", cex=0.85)
text(27.5,20,labels=bquote(y== .(8)*x - .(150)),col="red", cex=0.85)

Answer 1

Попробуй это:

reg_lin_int <- reg_lin$coefficients[1]
reg_lin_slp <- reg_lin$coefficients[2]

sum((y1 - (reg_lin_int + reg_lin_slp*x1)) ^ 2)
# [1] 39486.33
sum((y1 - (-150 + 8 * x1)) ^ 2)
# [1] 55583.18

Сумма квадратов остатков ниже под lm подходящая линия. Этого следовало ожидать, так как reg_lin_int а также reg_lin_slp гарантированно производить минимальную общую квадратическую ошибку.

Интуитивно, мы знаем, что оценки при квадратичных функциях потерь чувствительны к выбросам. Она "пропускает" группу внизу, потому что она приближается к группе вверху слева, что намного дальше - и квадрат расстояния дает этим точкам больший вес.

На самом деле, если мы используем регрессию наименьших абсолютных отклонений (т. Е. Указываем функцию абсолютных потерь вместо квадрата), результат будет намного ближе к вашему предположению:

library(quantreg)
lad_reg <- rq(y1 ~ x1)

(Pro совет: использовать lwd чтобы сделать ваши графики намного более читабельными)

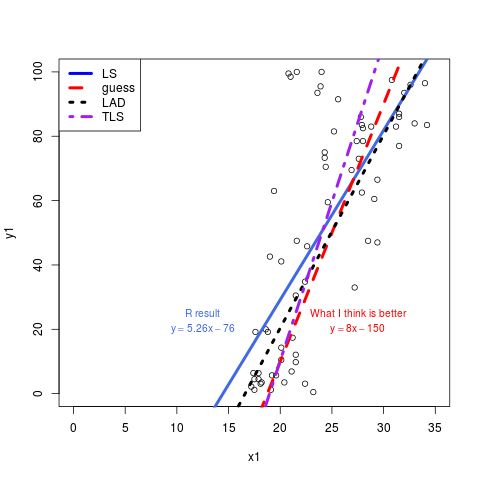
Что еще ближе к тому, что вы имели в виду, так это Total Least Squares, о чем упоминали @nongkrong и @MikeWilliamson. Вот результат TLS на вашем образце:

v <- prcomp(cbind(x1, y1))$rotation
bbeta <- v[-ncol(v), ncol(v)] / v[1, 1]
inter <- mean(y1) - bbeta * mean(x1)

Answer 2

Вы уже получили хороший ответ, но, возможно, это также полезно:

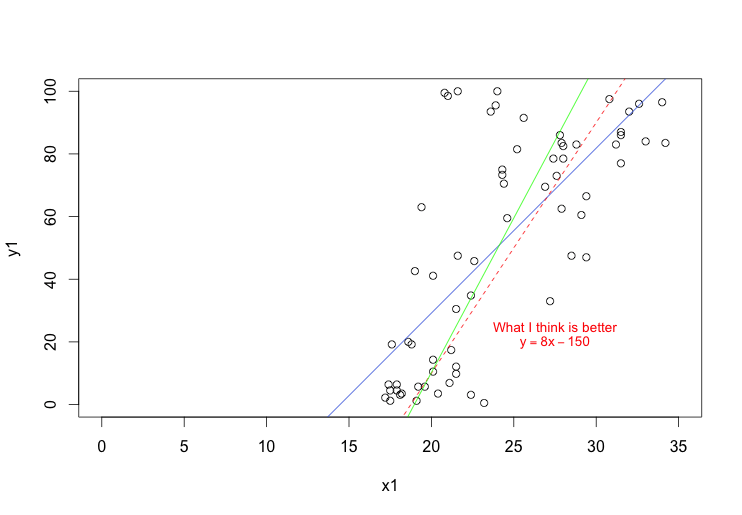
Как вы знаете, OLS минимизирует сумму квадратов ошибок в направлении y. Это подразумевает, что неопределенность ваших значений x незначительна, что часто имеет место. Но, возможно, дело не в ваших данных. Если предположить, что неопределенности в x и y равны, и выполнить регрессию Деминга, мы получим соответствие, более похожее на то, что вы ожидали.

library(MethComp)
dem_reg <- Deming(x1, y1)
abline(dem_reg[1:2], col = "green")

Вы не предоставляете подробную информацию о ваших данных. Таким образом, это может быть полезно или нет.