Создать случайную форму / контур, используя Matplotlib
Я пытаюсь создать изображение случайного контура с помощью Python, но я не мог найти простой способ сделать это.
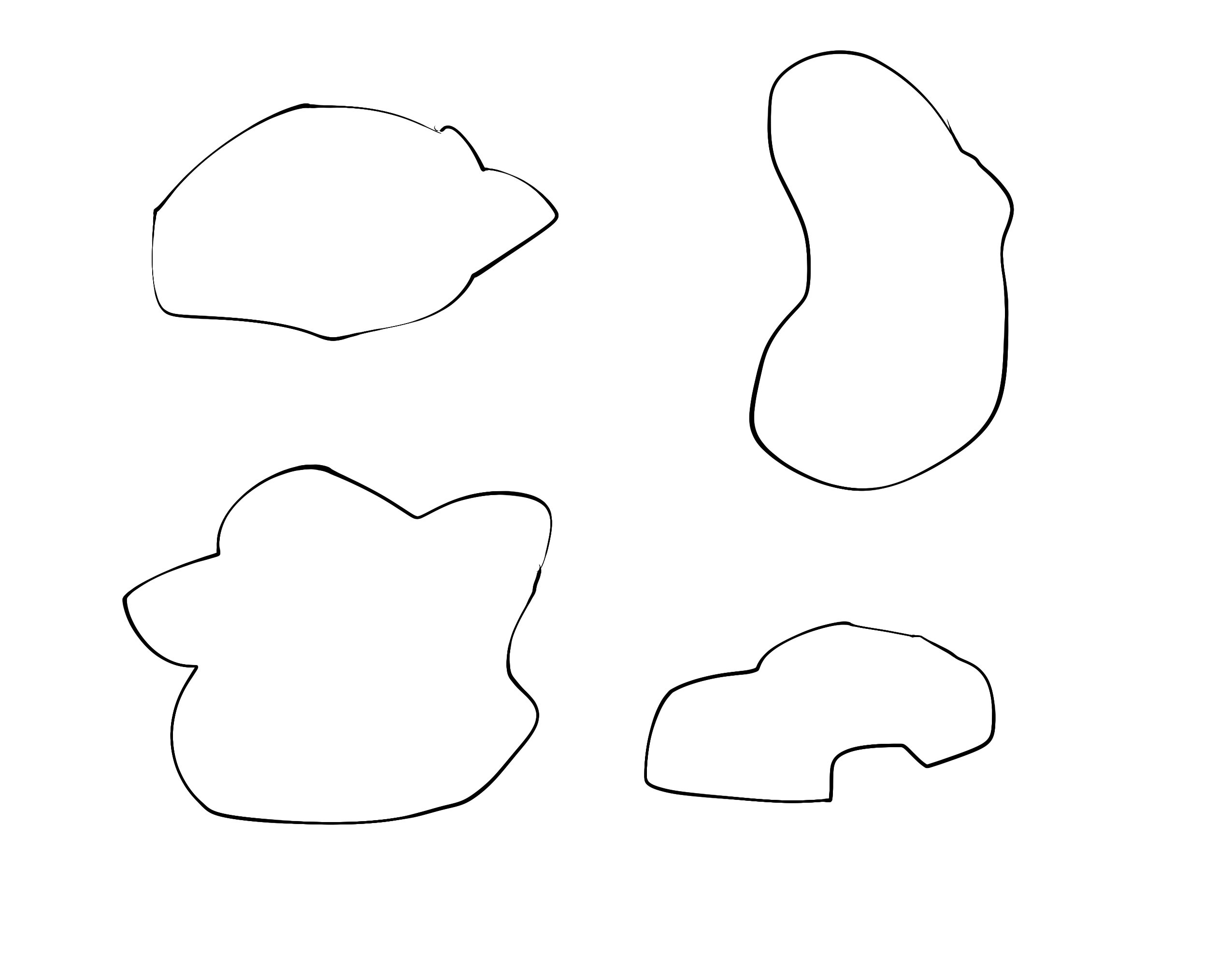
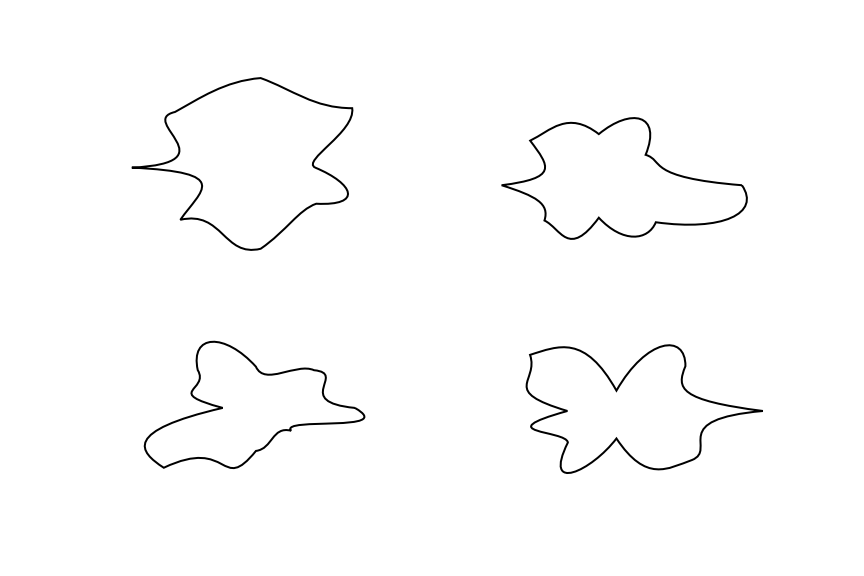
Вот пример того, что я хочу:
Первоначально я пытался сделать это с помощью функций matplotlib и gaussian, но я даже не мог приблизиться к изображению, которое я показал.
Есть ли простой способ сделать это?
Я ценю любую помощь
3 ответа
Matplotlib Path
Простой способ получить случайные и довольно сглаженные формы - использовать модуль matplotlib.path.
Используя кубическую кривую Безье, большинство линий будут сглажены, и число острых граней будет одним из параметров для настройки.
Шаги будут следующие. Сначала определяются параметры формы, это количество острых граней n и максимальное возмущение относительно положения по умолчанию в единичном круге r, В этом примере точки перемещаются из единичного круга с радиальной коррекцией, которая изменяет радиус от 1 до случайного числа между 1-r,1+r,
Вот почему вершины определяются как синус или косинус соответствующего угла, умноженного на коэффициент радиуса, чтобы поместить точки в окружность и затем изменить их радиус, чтобы ввести случайную составляющую. stack, .T транспонировать и [:,None] предназначены только для преобразования массивов во входные данные, принятые matplotlib.
Ниже приведен пример использования этого вида радиальной коррекции:
from matplotlib.path import Path
import matplotlib.patches as patches
n = 8 # Number of possibly sharp edges
r = .7 # magnitude of the perturbation from the unit circle,
# should be between 0 and 1
N = n*3+1 # number of points in the Path
# There is the initial point and 3 points per cubic bezier curve. Thus, the curve will only pass though n points, which will be the sharp edges, the other 2 modify the shape of the bezier curve
angles = np.linspace(0,2*np.pi,N)
codes = np.full(N,Path.CURVE4)
codes[0] = Path.MOVETO
verts = np.stack((np.cos(angles),np.sin(angles))).T*(2*r*np.random.random(N)+1-r)[:,None]
verts[-1,:] = verts[0,:] # Using this instad of Path.CLOSEPOLY avoids an innecessary straight line
path = Path(verts, codes)
fig = plt.figure()
ax = fig.add_subplot(111)
patch = patches.PathPatch(path, facecolor='none', lw=2)
ax.add_patch(patch)
ax.set_xlim(np.min(verts)*1.1, np.max(verts)*1.1)
ax.set_ylim(np.min(verts)*1.1, np.max(verts)*1.1)
ax.axis('off') # removes the axis to leave only the shape
Для чего n=8 а также r=0.7 производит такие формы:
Фильтрованный по Гауссу путь matplotlib
Существует также возможность генерирования фигуры с кодом выше для одной фигуры, а затем использовать scipy для выполнения гауссовой фильтрации сгенерированного изображения.
Основная идея выполнения гауссовского фильтра и извлечения сглаженной формы заключается в создании заполненной формы; сохранить изображение в виде 2-мерного массива (значения которого будут между 0 и 1, поскольку это будет изображение в оттенках серого); затем примените фильтр Гаусса; и в конечном итоге, получить сглаженную форму в виде 0,5 контура отфильтрованного массива.
Поэтому эта вторая версия будет выглядеть так:
# additional imports
from skimage import color as skolor # see the docs at scikit-image.org/
from skimage import measure
from scipy.ndimage import gaussian_filter
sigma = 7 # smoothing parameter
# ...
path = Path(verts, codes)
ax = fig.add_axes([0,0,1,1]) # create the subplot filling the whole figure
patch = patches.PathPatch(path, facecolor='k', lw=2) # Fill the shape in black
# ...
ax.axis('off')
fig.canvas.draw()
##### Smoothing ####
# get the image as an array of values between 0 and 1
data = data = np.frombuffer(fig.canvas.tostring_rgb(), dtype=np.uint8)
data = data.reshape(fig.canvas.get_width_height()[::-1] + (3,))
gray_image = skolor.rgb2gray(data)
# filter the image
smoothed_image = gaussian_filter(gray_image,sigma)
# Retrive smoothed shape as 0.5 contour
smooth_contour = measure.find_contours(smoothed_image[::-1,:], 0.5)[0]
# Note, the values of the contour will range from 0 to smoothed_image.shape[0]
# and likewise for the second dimension, if desired,
# they should be rescaled to go between 0,1 afterwards
# compare smoothed ans original shape
fig = plt.figure(figsize=(8,4))
ax1 = fig.add_subplot(1,2,1)
patch = patches.PathPatch(path, facecolor='none', lw=2)
ax1.add_patch(patch)
ax1.set_xlim(np.min(verts)*1.1, np.max(verts)*1.1)
ax1.set_ylim(np.min(verts)*1.1, np.max(verts)*1.1)
ax1.axis('off') # removes the axis to leave only the shape
ax2 = fig.add_subplot(1,2,2)
ax2.plot(smooth_contour[:, 1], smooth_contour[:, 0], linewidth=2, c='k')
ax2.axis('off')
Проблема в том, что вид случайных фигур, показанных в вопросе, не является действительно случайным. Они как-то сглажены, упорядочены, на вид случайные формы. Хотя создавать действительно случайные формы с помощью компьютера легко, создание этих псевдослучайных форм намного проще, если использовать ручку и бумагу.
Следовательно, одним из вариантов является создание таких форм в интерактивном режиме. Это показано в вопросе Интерактивная примерка BSpline в Python.
Если вы хотите создавать случайные фигуры программно, мы можем адаптировать решение к тому, как соединять точки с учетом положения и ориентации каждой из них, используя кубические кривые Безье.
Идея состоит в том, чтобы создать набор случайных точек с помощью get_random_points и вызвать функцию get_bezier_curve с этими. Это создает набор кривых Безье, которые плавно связаны друг с другом в точках ввода. Мы также следим за тем, чтобы они были циклическими, то есть чтобы переход между начальной и конечной точкой также был плавным.
import numpy as np
from scipy.special import binom
import matplotlib.pyplot as plt
bernstein = lambda n, k, t: binom(n,k)* t**k * (1.-t)**(n-k)
def bezier(points, num=200):
N = len(points)
t = np.linspace(0, 1, num=num)
curve = np.zeros((num, 2))
for i in range(N):
curve += np.outer(bernstein(N - 1, i, t), points[i])
return curve
class Segment():
def __init__(self, p1, p2, angle1, angle2, **kw):
self.p1 = p1; self.p2 = p2
self.angle1 = angle1; self.angle2 = angle2
self.numpoints = kw.get("numpoints", 100)
r = kw.get("r", 0.3)
d = np.sqrt(np.sum((self.p2-self.p1)**2))
self.r = r*d
self.p = np.zeros((4,2))
self.p[0,:] = self.p1[:]
self.p[3,:] = self.p2[:]
self.calc_intermediate_points(self.r)
def calc_intermediate_points(self,r):
self.p[1,:] = self.p1 + np.array([self.r*np.cos(self.angle1),
self.r*np.sin(self.angle1)])
self.p[2,:] = self.p2 + np.array([self.r*np.cos(self.angle2+np.pi),
self.r*np.sin(self.angle2+np.pi)])
self.curve = bezier(self.p,self.numpoints)
def get_curve(points, **kw):
segments = []
for i in range(len(points)-1):
seg = Segment(points[i,:2], points[i+1,:2], points[i,2],points[i+1,2],**kw)
segments.append(seg)
curve = np.concatenate([s.curve for s in segments])
return segments, curve
def ccw_sort(p):
d = p-np.mean(p,axis=0)
s = np.arctan2(d[:,0], d[:,1])
return p[np.argsort(s),:]
def get_bezier_curve(a, rad=0.2, edgy=0):
""" given an array of points *a*, create a curve through
those points.
*rad* is a number between 0 and 1 to steer the distance of
control points.
*edgy* is a parameter which controls how "edgy" the curve is,
edgy=0 is smoothest."""
p = np.arctan(edgy)/np.pi+.5
a = ccw_sort(a)
a = np.append(a, np.atleast_2d(a[0,:]), axis=0)
d = np.diff(a, axis=0)
ang = np.arctan2(d[:,1],d[:,0])
f = lambda ang : (ang>=0)*ang + (ang<0)*(ang+2*np.pi)
ang = f(ang)
ang1 = ang
ang2 = np.roll(ang,1)
ang = p*ang1 + (1-p)*ang2 + (np.abs(ang2-ang1) > np.pi )*np.pi
ang = np.append(ang, [ang[0]])
a = np.append(a, np.atleast_2d(ang).T, axis=1)
s, c = get_curve(a, r=rad, method="var")
x,y = c.T
return x,y, a
def get_random_points(n=5, scale=0.8, mindst=None, rec=0):
""" create n random points in the unit square, which are *mindst*
apart, then scale them."""
mindst = mindst or .7/n
a = np.random.rand(n,2)
d = np.sqrt(np.sum(np.diff(ccw_sort(a), axis=0), axis=1)**2)
if np.all(d >= mindst) or rec>=200:
return a*scale
else:
return get_random_points(n=n, scale=scale, mindst=mindst, rec=rec+1)
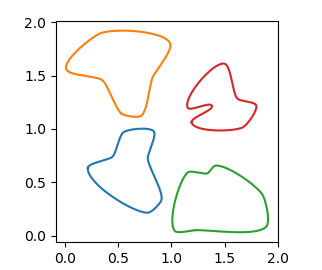
Вы можете использовать эти функции, например, как
fig, ax = plt.subplots()
ax.set_aspect("equal")
rad = 0.2
edgy = 0.05
for c in np.array([[0,0], [0,1], [1,0], [1,1]]):
a = get_random_points(n=7, scale=1) + c
x,y, _ = get_bezier_curve(a,rad=rad, edgy=edgy)
plt.plot(x,y)
plt.show()
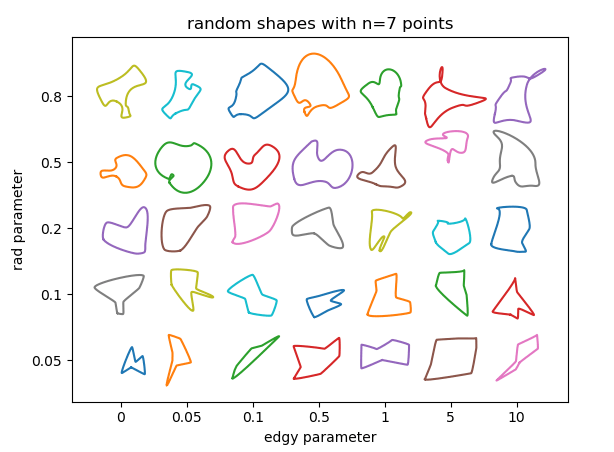
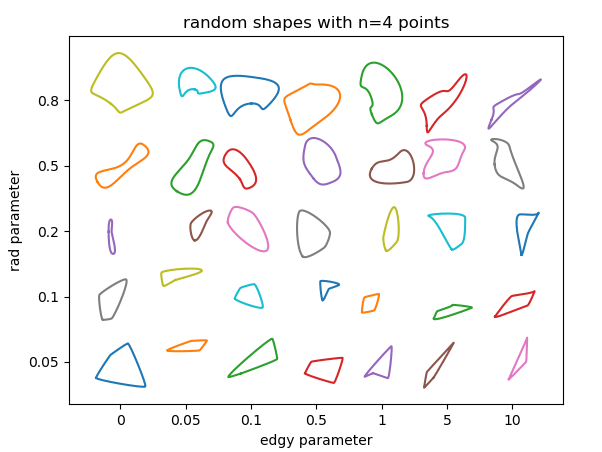
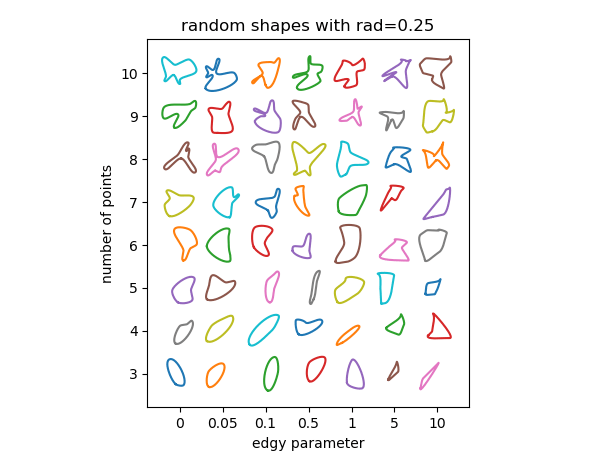
Мы можем проверить, как параметры влияют на результат. По сути, здесь нужно использовать 3 параметра:
radрадиус вокруг точек, в которых находятся контрольные точки кривой Безье. Это число относится к расстоянию между соседними точками и, следовательно, должно быть от 0 до 1. Чем больше радиус, тем четче черты кривой.edgyпараметр для определения гладкости кривой. Если 0, то угол кривой через каждую точку будет средним между направлением на соседние точки. Чем оно больше, тем больше угол будет определяться только одной соседней точкой. Кривая, следовательно, становится "более острой".nколичество случайных точек для использования. Конечно, минимальное количество очков - 3. Чем больше очков вы используете, тем больше возможностей получит форма; с риском создания наложений или петель на кривой.
Чтобы ответить на ваш вопрос, не существует простого способа сделать это. Генерирование случайных вещей, которые выглядят и ощущаются естественно, является гораздо более сложной проблемой, чем может показаться на первый взгляд, поэтому такие вещи, как перлин-шум, являются важными методами.
Любой традиционный программный подход (не включающий, скажем, нейронные сети), вероятно, закончился бы как сложный многоэтапный процесс выбора случайных точек, расстановки фигур, рисования линий и т. Д., Отрегулированных до тех пор, пока он не будет выглядеть так, как вы этого хотите. С таким подходом будет очень сложно получить что-либо, что надежно генерирует формы, такие же динамичные и органичные, как ваши примеры с нуля.
Если вас больше интересует результат, чем реализация, вы можете попробовать найти библиотеку, которая генерирует убедительно выглядящие гладкие случайные текстуры и вырезает из них контурные линии. Это единственный "легкий" подход, который приходит на ум прямо сейчас. Вот пример перлин-шума. Обратите внимание на формы, сформированные из уровней серого.