Решить ограниченное квадратичное программирование с помощью R

Question

Я действительно люблю R, но время от времени это действительно вызывает головную боль...

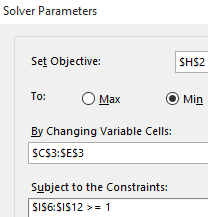
У меня есть следующая простая задача квадратичной минимизации, которая может быть быстро сформулирована и решена в Excel (нажмите на картинку для увеличения):

а также

Сама проблема довольно проста: я хочу минимизировать (w1^2+w2^2)/2 находя лучшую комбинацию w1,w2 а также b в условиях, которые для всех Y*(w1*X1+w2*X2+b) >= 1

Я знаю, что есть quadprog пакет для решения подобных проблем, но я нахожу его настолько не интуитивно понятным, что я не могу правильно указать проблему:-(Мне неприятно это говорить, но Excel, кажется, лучше подходит для определения таких задач оптимизации, как эти:-(((

Мой вопрос
Как правильно сформулировать вышеуказанную проблему, чтобы ее можно было решить с помощью R (независимо от того, какой пакет), и программа получит правильные значения для w1, w2 а также b (как видно на картинке выше). Пожалуйста, не просто публикуйте ссылки, но, пожалуйста, дайте действующий код. Было бы здорово, если бы вы могли прокомментировать свой код, чтобы стало понятно, почему вы делаете то, что делаете. Спасибо!

Необходимые данные здесь:

data <- matrix(c(2.947814,6.626878, 1,
                 2.530388,7.785050, 1,
                 3.566991,5.651046, 1,
                 3.156983,5.467077, 1,
                 2.582346,4.457777,-1,
                 2.155826,6.222343,-1,
                 3.273418,3.520687,-1),ncol=3,byrow=T)
colnames(data) <- c("X1","X2","y")

добавление
Некоторые люди обиделись на мою просьбу предоставить код (а не просто ссылки). Я извинился за это и объяснил причины, по которым я не нашел хороших подходов в ответах на SO. Более глубокая причина этого заключается в том, что проблема необычна в том смысле, что b находится только в ограничении, а не в целевой функции. Поэтому я все еще думаю, что этот вопрос хорошо подходит для SO.

Answer 1

На самом деле, проблема немного сложнее, потому что b присутствует только в матрице ограничения неравенства, но не в целевой функции. Поэтому матрица в задаче квадратичного программирования является только положительной полуопределенной, но не положительно определенной.

Поэтому мой подход состоит в том, чтобы установить запись матрицы, соответствующую b в очень маленькое значение - в моем случае 1e-9, Кто-то еще, более знакомый с такими проблемами оптимизации, может знать, как решить проблему должным образом...

подсчитывать solve.QP вход

c1=data[,"X1"]*data[,"y"]
c2=data[,"X2"]*data[,"y"]

#I use 1e-9 for the b entry
Dmat=matrix(`[<-`(numeric(9),c(1,5,9),c(1,1,1e-9)),3,3)
dvec=rep(0,3)
Amat=cbind(c1,c2,data[,"y"])
bvec=rep(1,nrow(Amat))

Решить с solve.QP

library(quadprog)
sol=solve.QP(Dmat=Dmat,dvec=dvec,Amat=t(Amat),bvec=bvec)$solution
sol
#[1]   2.903910   1.201258 -14.734964

Так же, как Excel.

Answer 2

На будущее: эту проблему также можно решить вполне интуитивно, используяCVXRпакет, который предоставляет интерфейс для решения задач выпуклой оптимизации в R:

      # Install and load the CVXR package
if (!requireNamespace("CVXR", quietly = TRUE)) {
  install.packages("CVXR")
}
library(CVXR)
# Define the data
data <- matrix(c(2.947814,6.626878, 1,
                 2.530388,7.785050, 1,
                 3.566991,5.651046, 1,
                 3.156983,5.467077, 1,
                 2.582346,4.457777,-1,
                 2.155826,6.222343,-1,
                 3.273418,3.520687,-1), ncol = 3, byrow = T)
colnames(data) <- c("X1", "X2", "y")

# Define the variables and parameters
w <- Variable(2)
b <- Variable()

# Define the constraints
constraints <- list()
for (i in 1:nrow(data)) {
  constraints[[i]] <- data[i, "y"] * (sum(data[i, 1:2] * w) + b) >= 1
}

# Define the objective function
objective <- Minimize(sum(w^2)/2)

# Solve the problem
problem <- Problem(objective, constraints)
result <- solve(problem)

# Print the results
cat("w1:", result$getValue(w)[1], "\nw2:", result$getValue(w)[2], "\nb:", result$getValue(b))
## w1: 2.90391 
## w2: 1.201258 
## b: -14.73496