Самый эффективный способ выбрать точку с наиболее окружающими точками

Question

NB: в нижней части вопроса есть серьезное редактирование - проверьте это

Вопрос

Скажем, у меня есть набор точек:

Я хочу найти точку с наибольшим количеством точек вокруг нее в радиусе (то есть круг) или внутри (т.е. квадрат) точки для 2-х измерений. Я буду называть это самой плотной точечной функцией.

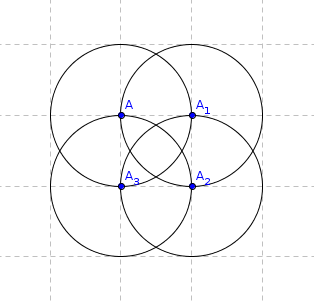
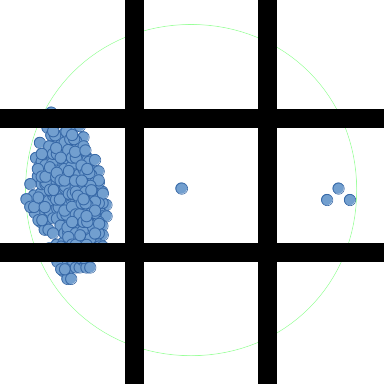
Для диаграмм в этом вопросе я буду представлять окружающий регион в виде кругов. На изображении выше, окружающая область средней точки показана зеленым цветом. Эта средняя точка имеет большинство окружающих точек из всех точек в радиусе и будет возвращен самой плотной точечной функцией.

Что я пробовал

Эффективным способом решения этой проблемы было бы использование решения поиска диапазона; этот ответ объясняет дальше и что он имеет " наихудшее время ". Используя это, я мог бы получить количество точек, окружающих каждую точку, и выбрать точку с наибольшим количеством окружающих точек.

Однако, если точки были чрезвычайно плотно упакованы (порядка миллиона), как таковой:

тогда каждый из этих миллионов очков () необходимо выполнить поиск по диапазону. Наихудшее время , где количество точек, возвращаемых в диапазоне, верно для следующих типов дерева точек:

• КД-деревья двух измерений (которые на самом деле немного хуже, в ),
• Деревья 2d-диапазона,
• Quadtree, которые имеют худшее время

Итак, для группы точки в радиусе из всех точек в группе, это дает сложность за каждую точку. Это дает более триллиона операций!

Любые идеи о более эффективном и точном способе достижения этого, чтобы я мог найти точку с наиболее окружающими точками для группы точек и в разумные сроки (желательно или менее)?

РЕДАКТИРОВАТЬ

Оказывается, что приведенный выше метод является правильным! Мне просто нужна помощь в реализации.

(Полу-) Решение

Если я использую дерево 2d-диапазона:

• Диапазон отчетов о затратах на запрос , за возвращенные очки,
• Для дерева диапазонов с дробным каскадированием (также известного как слоистые деревья диапазонов) сложность ,
• Для 2-х измерений это ,
• Кроме того, если я выполняю запрос подсчета диапазона (т. Е. Я не сообщаю каждую точку), то это стоит ,

Я выполнил бы это в каждой точке - получая сложность, которую я желал!

проблема

Однако я не могу понять, как написать код для запроса подсчета для двухуровневого дерева диапазонов.

Я нашел отличный ресурс (начиная со страницы 113) о деревьях диапазонов, включая psuedocode дерева 2d-диапазона. Но я не могу понять, как ввести дробное каскадирование или как правильно реализовать запрос подсчета, чтобы он O(log n) сложность.

Я также нашел две реализации дерева диапазонов здесь и здесь в Java, и одну в C++ здесь, хотя я не уверен, что здесь используется дробный каскад, как указано выше countInRange метод, который

Возвращает количество таких точек в худшем случае * O(log(n)^d) раз. Он также может возвращать точки, которые находятся в прямоугольнике в худшем случае * O(log(n)^d + k) время, где k - количество точек, лежащих в прямоугольнике.

который предлагает мне, он не применяет дробное каскадирование.

Уточненный вопрос

Поэтому, чтобы ответить на поставленный выше вопрос, все, что мне нужно знать, - это наличие библиотек с деревьями 2-го диапазона с дробным каскадом, имеющих сложный запрос на подсчет диапазона так что я не буду изобретать новые колеса, или вы можете помочь мне написать / изменить вышеупомянутые ресурсы для выполнения запроса такой сложности?

Также не жалуюсь, если вы можете предоставить мне какие-либо другие методы для выполнения запроса подсчета диапазона 2d точек в любым другим способом!

Answer 1

Я предлагаю использовать алгоритм плоской развертки. Это позволяет одномерные запросы диапазона вместо двумерных запросов. (Что более эффективно, проще и в случае квадратной окрестности не требует дробного каскадирования):

1. Сортировать точки по Y-координате в массив S.
2. Продвиньте 3 указателя на массив S: один (C) для текущей проверяемой (центральной) точки; другой, A (немного впереди) для ближайшей точки на расстоянии> R ниже C; и последний, B (немного позади) для самой дальней точки на расстоянии
3. Вставьте точки, обозначенные буквой A, чтобы упорядочить статистическое дерево (упорядоченное по координате X) и удалите точки, обозначенные буквой B, из этого дерева. Используйте это дерево, чтобы найти точки на расстоянии R влево / вправо от C и использовать разность позиций этих точек в дереве, чтобы получить количество точек в квадратной области вокруг C.
4. Используйте результаты предыдущего шага, чтобы выбрать "наиболее окруженную" точку.

Этот алгоритм может быть оптимизирован, если вы поворачиваете точки (или просто меняете координаты XY), чтобы ширина занятой области не превышала ее высоту. Также вы можете разрезать точки на вертикальные срезы (с перекрытием размера R) и обрабатывать срезы по отдельности - если в дереве слишком много элементов, чтобы оно не помещалось в кэш-память ЦП (что маловероятно только для 1 миллиона точек). Этот алгоритм (оптимизированный или нет) имеет временную сложность O(n log n).

Для круговой окрестности (если R не слишком велико и точки распределены равномерно), вы можете аппроксимировать окружность несколькими прямоугольниками:

В этом случае шаг 2 алгоритма должен использовать больше указателей, чтобы разрешить вставку / удаление в / из нескольких деревьев. И на шаге 3 вы должны выполнить линейный поиск вблизи точек на правильном расстоянии (<=R), чтобы отличить точки внутри круга от точек за его пределами.

Другой способ справиться с круговой окрестностью - это аппроксимировать круг прямоугольниками одинаковой высоты (но здесь круг должен быть разбит на несколько частей). Это приводит к гораздо более простому алгоритму (где вместо деревьев статистики порядка используются отсортированные массивы):

1. Вырезать область, занимаемую точками, на горизонтальные срезы, отсортировать срезы по Y, затем отсортировать точки внутри срезов по X.
2. Для каждой точки в каждом срезе, предположим, что это "центральная" точка, и выполните шаг 3.
3. Для каждого соседнего среза используйте бинарный поиск, чтобы найти точки с евклидовым расстоянием, близким к R, затем используйте линейный поиск, чтобы отличить "внутренние" точки от "внешних". Остановите линейный поиск, когда срез полностью находится внутри круга, и подсчитайте оставшиеся точки по разности позиций в массиве.
4. Используйте результаты предыдущего шага, чтобы выбрать "наиболее окруженную" точку.

Этот алгоритм позволяет оптимизации, упомянутые ранее, а также дробное каскадирование.

Answer 2

Я бы начал с создания чего-то вроде https://en.wikipedia.org/wiki/K-d_tree, где у вас есть дерево с точками на листьях и каждым узлом с информацией о его потомках. На каждом узле я бы вел подсчет количества потомков и ограничивающую рамку, заключающую в себе этих потомков.

Теперь для каждой точки я бы рекурсивно искал дерево. На каждом узле, который я посещаю, либо все ограничивающие рамки находятся в пределах R от текущей точки, либо все ограничивающие рамки находятся на расстоянии более R от текущей точки, либо некоторые из них находятся внутри R, а некоторые - за пределами R. В первом В этом случае я могу использовать счетчик числа потомков текущего узла, чтобы увеличить количество точек в пределах R текущей точки и вернуться на один уровень рекурсии. Во втором случае я могу просто вернуться на один уровень рекурсии, ничего не увеличивая. Только в промежуточном случае мне нужно продолжать возвращаться вниз по дереву.

Таким образом, я могу определить для каждой точки количество соседей в пределах R, не проверяя каждую другую точку, и выбрать точку с наибольшим количеством.

Если точки распределены равномерно, то я думаю, что в итоге вы построите дерево kd, где нижние уровни будут близки к регулярной сетке, и я думаю, что если сетка имеет размер A x A, то в худшем случае R достаточно велик так что его граница представляет собой круг, который пересекает ячейки низкого уровня O(A), поэтому я думаю, что если у вас есть O(n) точек, вы можете ожидать, что это будет стоить около O(n * sqrt(n)).

Answer 3

Вы можете ускорить любой алгоритм, который вы используете, предварительно обработав ваши данные в O(n) время, чтобы оценить количество соседних точек.

Для круга радиуса R создайте сетку, ячейки которой имеют размерность R в направлениях x и y. Для каждой точки определите, к какой ячейке она принадлежит. Для данной ячейки c этот тест прост:

c.x<=p.x && p.x<=c.x+R && c.y<=p.y && p.y<=c.y+R

(Возможно, вы захотите глубоко задуматься о том, является ли правильный интервал закрытым или полуоткрытым.)

Если у вас относительно плотное / однородное покрытие, то вы можете использовать массив для хранения значений. Если покрытие редкое / разнородное, вы можете использовать хэш-карту.

Теперь рассмотрим точку на сетке. Экстремальные положения точки внутри ячейки такие, как указано:

Точки в углах ячейки могут быть только соседями с точками в четырех ячейках. Точки вдоль ребра могут быть соседями с точками в шести ячейках. Точки не на ребре - это соседи с точками в 7-9 ячеек. Поскольку точка редко падает точно на угол или ребро, мы предполагаем, что любая точка в фокальной ячейке является соседней с точками во всех 8 окружающих ячейках.

Итак, если точка p находится в ячейке (x, y), N[p] определяет количество соседей p в радиусе R и Np[y][x] обозначает количество точек в ячейке (х, у), тогда N[p] дан кем-то:

N[p] = Np[y][x]+
       Np[y][x-1]+
       Np[y-1][x-1]+
       Np[y-1][x]+
       Np[y-1][x+1]+
       Np[y][x+1]+
       Np[y+1][x+1]+
       Np[y+1][x]+
       Np[y+1][x-1]

После того, как мы оценили число соседей для каждой точки, мы можем преобразовать эту структуру данных в макси-кучу в O(n) время (например, make_heap). Структура теперь является приоритетной очередью, и мы можем получить точки за O(log n) за каждый запрос, упорядоченный по их оценочному количеству соседей.

Сделайте это для первой точки и используйте O(log n + k) круговой поиск (или какой-нибудь более умный алгоритм), чтобы определить фактическое количество соседей, которые имеет точка. Запишите этот момент в переменной best_found и обновить его N[p] значение.

Заглянуть на вершину кучи. Если предполагаемое количество соседей меньше N[best_found] тогда мы закончили. В противном случае повторите вышеописанную операцию.

Для улучшения оценок вы можете использовать более точную сетку, например:

наряду с некоторыми умными методами скользящего окна, чтобы уменьшить объем требуемой обработки (см., например, этот ответ для прямоугольных случаев - для круглых окон вы, вероятно, должны использовать коллекцию очередей FIFO). Для повышения безопасности вы можете рандомизировать происхождение сетки.

Рассмотрим снова пример, который вы изложили:

Ясно, что эта эвристика имеет потенциал для экономии значительного времени: при использовании вышеупомянутой сетки потребуется только одна дорогая проверка, чтобы доказать, что в средней точке больше всего соседей. Опять же, сетка с более высоким разрешением улучшит оценки и уменьшит количество дорогостоящих проверок, которые необходимо сделать.

Вы можете и должны использовать аналогичную ограничивающую технику вместе с mcdowella; однако, его ответ не дает хорошего места, чтобы начать искать, поэтому можно потратить много времени на изучение малоценных очков.