Нахождение всех точек в определенном радиусе другой точки
Я делаю простую игру и наткнулся на эту проблему. Предположим несколько точек в 2D пространстве. Я хочу, чтобы точки, расположенные близко друг к другу, каким-то образом взаимодействовали.
Позвольте мне бросить картинку здесь для лучшего понимания проблемы: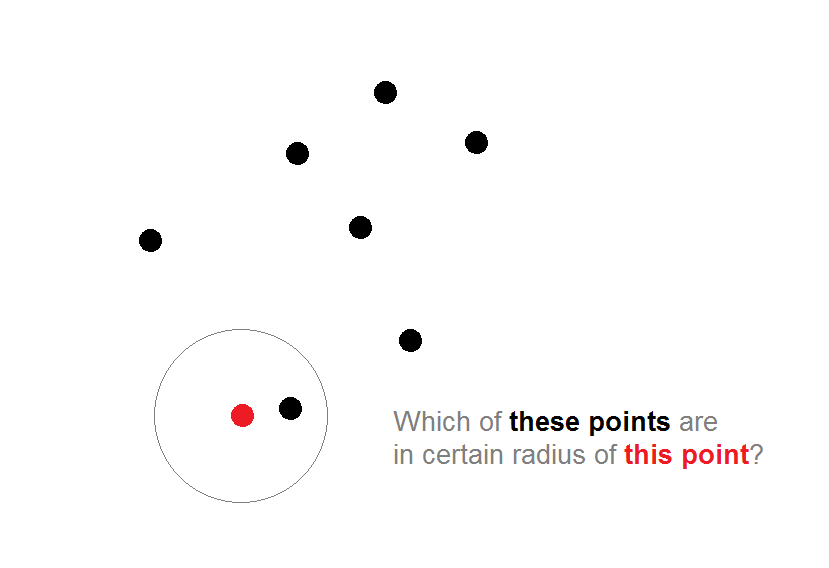
Теперь проблема не в вычислении расстояния. Я знаю, как это сделать.
Сначала у меня было около 10 очков, и я мог просто проверять каждую комбинацию, но, как вы уже можете предположить, это крайне неэффективно с увеличением количества очков. Что если бы у меня было всего миллион очков, но все они были бы очень далеки друг от друга?
Я пытаюсь найти подходящую структуру данных или способ взглянуть на эту проблему, так что каждая точка может иметь дело только с окружающим, а не с целым пространством. Есть ли известные алгоритмы для этого? Я точно не знаю, как назвать эту проблему, чтобы я мог точно сказать, что я хочу.
Если вы не знаете такого известного алгоритма, все идеи приветствуются.
5 ответов
Вам все еще придется перебирать каждую точку, но есть две оптимизации, которые вы можете выполнить:
1) Вы можете устранить очевидные точки, проверив, если x1 <радиус и y1 <радиус (как Брент уже упоминал в другом ответе).
2) Вместо вычисления расстояния вы можете рассчитать квадрат расстояния и сравнить его с квадратом допустимого радиуса. Это спасает вас от выполнения дорогостоящих вычислений квадратного корня.
Это, наверное, лучшее представление, которое ты получишь.
Это проблема поиска диапазона. Точнее говоря, проблема 2-мерного кругового диапазона.
Цитата из "Решение задач поиска-запроса путем сжатия диаграмм Вороного" [Aggarwal, Hansen, Leighton, 1990]:
- Вход: набор P из n точек на евклидовой плоскости E²
- Запрос: Найти все точки P, содержащиеся в диске в E² с радиусом r с центром в q.
Наилучшие результаты были получены в "Отчете об оптимальном диапазоне полупространства в трех измерениях" [Afshani, Chan, 2009]. Их метод требует O(n) пространственной структуры данных, которая поддерживает запросы за O(log n + k) наихудшего времени. Структура может быть предварительно обработана с помощью рандомизированного алгоритма, который выполняется за ожидаемое время O(n log n). (n - количество входных точек, а k - количество выходных точек).
Библиотека CGAL поддерживает круговые поисковые запросы. Смотрите здесь.
Разделение пространства - это то, что вы хотите.. https://en.wikipedia.org/wiki/Quadtree
Это похоже на проблему ближайшего соседа. Вы должны использовать дерево kd для хранения точек.
Если бы вы могли отсортировать эти точки по значениям x и y, то вы могли бы быстро выбрать те точки (бинарный поиск?), Которые находятся в поле центральной точки: x +- r, y +- r. Если у вас есть это подмножество точек, вы можете использовать формулу расстояния, чтобы увидеть, находятся ли они в радиусе.
Я полагаю, у вас есть минимальные и максимальные координаты X и Y? Если так, то как насчет этого.
Назовите наш радиус R, Xmax-Xmin X и Ymax-Ymin Y.
Имейте 2D матрицу [X/R, Y/R] двойных списков. Поместите каждую точечную структуру в правильный связанный список.
Чтобы найти точки, с которыми вам нужно взаимодействовать, вам нужно только проверить свою ячейку и 8 соседей.
Пример: если X и Y равны 100, а R равно 1, поместите точку в ячейке 43,2, 77,1 [43,77]. Вы проверите ячейки [42,76] [43,76] [44,76] [42,77] [43,77] [44,77] [42,78] [43,78] [44,78] для матчей. Обратите внимание, что не все ячейки в вашем собственном ящике будут совпадать (например, 43,9,77,9 находится в том же списке, но на расстоянии более 1 единицы), и вам всегда нужно будет проверять все 8 соседей.
Когда точки движутся (кажется, что они будут двигаться?), Вы просто отсоедините их (быстро и легко с помощью списка двойных ссылок) и снова перейдете на новое место. Перемещение любой точки O(1). Перемещение их всех - O(n).
Если этот размер массива дает слишком много ячеек, вы можете сделать ячейки большего размера с тем же алгоритмом и, возможно, с тем же кодом; просто будьте готовы к тому, чтобы меньше точек-кандидатов были на самом деле достаточно близки. Например, если R=1 и карта в миллион раз R в миллион раз R, вы не сможете сделать 2D-массив таким большим. Может быть, лучше, чтобы каждая клетка имела ширину 1000 единиц? Пока плотность была низкой, вероятно, будет работать тот же код, что и раньше: проверяйте каждую точку только на соответствие другим точкам в этой ячейке и соседним 8 ячейкам. Просто будьте готовы к тому, что больше кандидатов не попадет в R.
Если в некоторых ячейках будет много точек, каждая ячейка имеет связанный список, возможно, в ячейке должно быть красно-черное дерево, индексированное по координате X? Даже в той же самой ячейке подавляющее большинство других членов ячейки будет слишком далеко, поэтому просто пересеките дерево от XR до X+R. Вместо того, чтобы перебирать все точки и углубляться в дерево каждого, возможно, вы могли бы вместо этого перебирать дерево, ища координаты X внутри R, и если / когда вы найдете их, рассчитать расстояние. Когда вы пересекаете дерево одной ячейки от низкого к высокому X, вам нужно только проверить соседнюю ячейку на дереве слева, пока в первых записях R.
Вы также можете пойти в ячейки меньше R. У вас будет меньше кандидатов, которые не смогут быть достаточно близко. Например, с R/2, вы должны проверить 25 списков ссылок вместо 9, но иметь в среднем (если распределено случайным образом) 25/36-е столько точек, чтобы проверить. Это может быть незначительным приобретением.