Nlinfit выглядит лучше, чем fitgmdist для подгонки нормальной смеси

Question

У меня есть вектор данных, состоящий из примерно 2 миллионов образцов, которые, как я подозреваю, представляют собой смесь двух гауссовских данных. Я пытаюсь подогнать данные, данные, к смеси, используя fitgmdist от Matlab.

Из гистограммы:

% histogram counts of X with 1000 bins.
[Yhist, x] = histcounts(Data, 1000, 'normalization', 'pdf');
x = (x(1:end-1) + x(2:end))/2;

Используя fitgmdist:

% Increase no. of iterations. default is 100.
opts.MaxIter = 300;

% Ensure that it does all iterations.
opts.TolFun = 0;

GMModel = fitgmdist(Data, 2, 'Options', opts, 'Start', 'plus');
wts = GMModel.ComponentProportion;
mu = GMModel.mu;
sig = sqrt(squeeze(GMModel.Sigma));
Ygmfit = wts(1)*normpdf(x(:), mu(1), sig(1)) + wts(2)*normpdf(x(:), mu(2), sig(2));

Результаты смешивания с fitgmdist: wts = [0,6780, 0,322], mu = [-7,6444, -9,7831], sig = [0,8243, 0,5947]

Далее я пытаюсь использовать nlinfit:

% Define the callback function for nlinfit.
function y = nmmix(a, x)
   a(1:2) = a(1:2)/sum(a);
   y = a(1)*normpdf(x(:), a(3), a(5)) + a(2)*normpdf(x(:), a(4), a(6));
end

init_wts = [0.66, 1-0.66];
init_mu = [-7.7, -9.75];
init_sig = [0.5, 0.5];
a = nlinfit(x(:), Yhist(:), @nmmix, [init_wts, init_mu, init_sig]);
wts = a(1:2)/sum(a(1:2));
mu = a(3:4);
sig = a(5:6);
Ynlinfit = wts(1)*normpdf(x(:), mu(1), sig(1)) + wts(2)*normpdf(x(:), mu(2), sig(2));

Результаты смешивания с nlinfit: wts = [0,6349, 0,3651], mu = [-7,6305, -9,6991], sig = [0,6773, 0,6031]

% Plot to compare the results
figure;
hold on
plot(x(:), Yhist, 'b');
plot(x(:), Ygmfit, 'k');
plot(x(:), Ynlinfit, 'r');

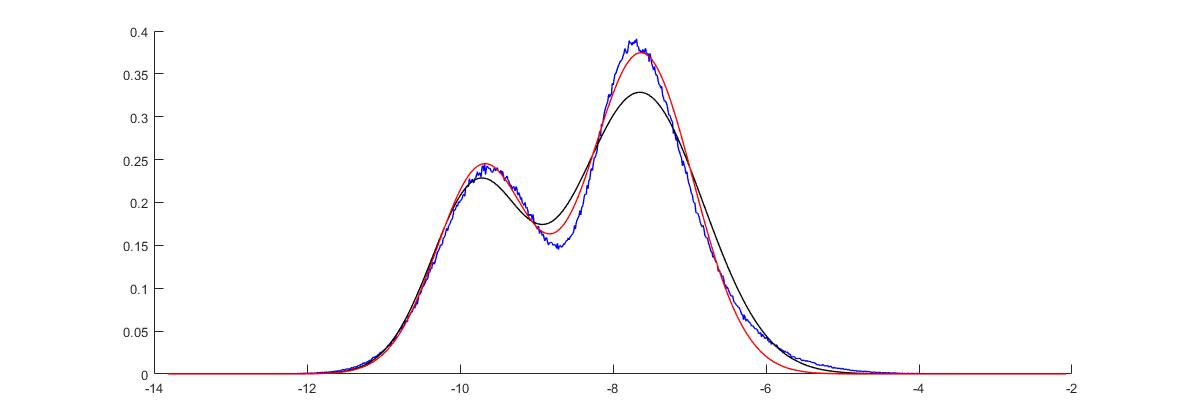
Похоже, что нелинейное соответствие (красная кривая) является интуитивно лучшим приближением к гистограмме (синяя кривая), чем "fitgmdist" (черная кривая). Результаты схожи, даже если я использую более точную гистограмму, скажем, с 100 000 бинов.

Что может быть источником этого несоответствия?

Добавлено позже: Конечно, нельзя ожидать, что результаты будут одинаковыми, но я ожидаю, что визуальное качество этих двух подгонок будет сопоставимым.