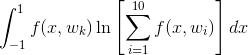NumPy векторизация с интеграцией
У меня есть вектор 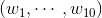 и хотим сделать еще один вектор такой же длины, чей k-й компонент
и хотим сделать еще один вектор такой же длины, чей k-й компонент
Вопрос: как мы можем векторизовать это для скорости? NumPy vectorize() на самом деле является циклом for, поэтому он не считается.
Ведрак отметил, что " нет способа применить чистую функцию Python к каждому элементу массива NumPy, не вызывая его столько раз". Поскольку я использую функции NumPy, а не "чистый Python", я полагаю, что возможно векторизовать, но я не знаю как.
import numpy as np
from scipy.integrate import quad
ws = 2 * np.random.random(10) - 1
n = len(ws)
integrals = np.empty(n)
def f(x, w):
if w < 0: return np.abs(x * w)
else: return np.exp(x) * w
def temp(x): return np.array([f(x, w) for w in ws]).sum()
def integrand(x, w): return f(x, w) * np.log(temp(x))
## Python for loop
for k in range(n):
integrals[k] = quad(integrand, -1, 1, args = ws[k])[0]
## NumPy vectorize
integrals = np.vectorize(quad)(integrand, -1, 1, args = ws)[0]
Следует отметить, что цикл Cython for всегда быстрее, чем векторизация NumPy?
2 ответа
Функция quad выполняет адаптивный алгоритм, что означает, что вычисления, которые он выполняет, зависят от конкретной вещи, которая интегрируется. Это не может быть векторизовано в принципе.
В вашем случае for петля длиной 10 не является проблемой. Если программа занимает много времени, это потому, что интеграция занимает много времени, а не потому, что у вас есть for петля.
Когда вам абсолютно необходимо векторизовать интеграцию (не в примере выше), используйте неадаптивный метод с пониманием того, что может пострадать точность. Они могут быть непосредственно применены к двумерному массиву NumPy, полученному путем оценки всех ваших функций в некотором равномерно распределенном одномерном массиве (linspace). Вы должны будете сами выбрать пространство, так как методы не адаптивны.
- numpy.trapz - самый простой и наименее точный
- scipy.integrate.simps одинаково прост в использовании и более точен (правило Симпсона требует нечетного числа выборок, но метод также обходится и иметь четное число).
- scipy.integrate.romb в принципе имеет более высокую точность, чем Симпсон (для сглаживания данных), но для этого требуется количество выборок
2**n+1для некоторого целого числаn,
@zaq's ответ с упором на quad на месте. Итак, я посмотрю на некоторые другие аспекты проблемы.
В недавнем /questions/15731393/numpy-vectorize-ili-dot-vyiglyadit-glyuchno/15731403#15731403 я утверждаю, что vectorize имеет наибольшее значение, когда вам нужно применить механизм полного вещания к функции, которая принимает только скалярные значения. Ваш quad квалифицируется как принятие скалярных входных данных. Но вы перебираете только один массив, ws, x то, что передается вашим функциям, генерируется quad сам. quad а также integrand все еще являются функциями Python, даже если они используют numpy операции.
cython улучшает итерацию низкого уровня, вещи, которые он может преобразовать в C код. Ваша основная итерация находится на высоком уровне, вызывая импортированную функцию, quad, Cython не может коснуться или переписать это.
Вы могли бы ускорить integrand (и вниз) с cython, но сначала сосредоточиться на получении максимальной скорости от этого с регулярным numpy код.
def f(x, w):
if w < 0: return np.abs(x * w)
else: return np.exp(x) * w
С if w<0w должен быть скалярным. Можно ли написать так, чтобы он работал с массивом w? Если так, то
np.array([f(x, w) for w in ws]).sum()
может быть переписан как
fn(x, ws).sum()
В качестве альтернативы, так как оба x а также w скалярные, вы можете получить некоторое улучшение скорости с помощью math.exp и т. д. вместо np.exp, То же самое для log а также abs,
Я бы попробовал написать f(x,w) так что это занимает массивы для обоих x а также w, возвращая 2d результат. Если так, то temp а также integrand также будет работать с массивами. поскольку quad кормит скаляр x, это может не помочь, но с другими интеграторами это может иметь большое значение.
Если f(x,w) можно оценить на регулярной сетке NX10 x=np.linspace(-1,1,n) а также wsтогда интеграл (своего рода) просто требует пары суммирования по этому пространству.
Вы можете использовать quadpy для полностью векторизованных вычислений. Вам придется сначала адаптировать свою функцию, чтобы разрешить векторные входные данные, но это делается довольно легко:
import numpy as np
import quadpy
np.random.seed(0)
ws = 2 * np.random.random(10) - 1
def f(x):
out = np.empty((len(ws), *x.shape))
out0 = np.abs(np.multiply.outer(ws, x))
out1 = np.multiply.outer(ws, np.exp(x))
out[ws < 0] = out0[ws < 0]
out[ws >= 0] = out1[ws >= 0]
return out
def integrand(x):
return f(x) * np.log(np.sum(f(x), axis=0))
val, err = quadpy.quad(integrand, -1, +1, epsabs=1.0e-10)
print(val)
[0.3266534 1.44001826 0.68767868 0.30035222 0.18011948 0.97630376
0.14724906 2.62169217 3.10276876 0.27499376]