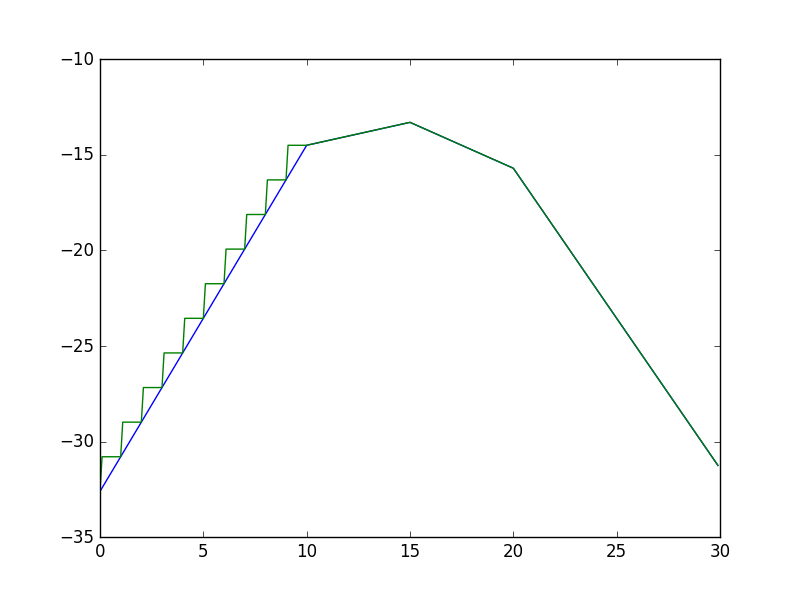
NumPy vectorize() или dot() выглядит глючно

Question

В приведенном ниже коде y1 и y2 должны быть равны, но это не так. Может ли быть ошибка в vectorize() или dot()?

import numpy as np
interval = np.arange(0, 30, 0.1)
y1 = [- 1.57 * max(0, x - 10) - 0.72 * max(0, 15 - x)
      - 1.09 * max(0, 20 - x) for x in interval]

def fun(x, pivot, truth):
    if truth: return max(0, x - pivot)
    else:     return max(0, pivot - x)

pivots = [10, 15, 20]
truths = [ 1,  0,  0]
coeffs = [-1.57, -0.72, -1.09]
y2 = [np.dot(np.vectorize(fun)(x, pivots, truths), coeffs) for x in interval]

import matplotlib.pyplot as plt
plt.plot(interval, y1, interval, y2)
plt.show()

Графики y1 и y2:

Answer 1

Чтобы применить правильные правила приведения, numpy иногда использует вашу функцию со значениями sentinel (numpy.int64), чтобы проверить, какие данные он выводит, если выводит целое число. 0 потому что вот что max затем возвращается, предполагается, что результат вычисления должен быть целым числом, и округляет остальные результаты, однако, если вы измените функцию, чтобы она всегда возвращала числа с плавающей запятой, используя 0.0 в макс:

def fun(x, pivot, truth):
    if truth: return max(0.0, x - pivot)
    else:     return max(0.0, pivot - x)

Тогда проверки, которые применяет numpy, всегда будут приводить к результатам с плавающей запятой, и округление не будет применяться.

Answer 2

Я не уверен, что это применимо в вашем случае, но vectorize есть несколько хитростей.

Если вы не укажете возврат dtype, он определяет это с помощью тестового расчета - с вашим первым случаем. Если ваша функция возвращает скалярное целое число, например 0, то vectorize возвращает целочисленный массив Так что если вы ожидаете поплавки, убедитесь, что вы указали возврат dtype,

Также - vectorize это не инструмент скорости. Это просто удобный способ применения трансляции к вашим входам. Это не намного быстрее, чем зацикливание на ваших входах.

np.vectorize(fun, otypes=[float])

удаляет шаги

===========

Попробуй это:

vfun = np.vectorize(fun, otypes=[float])
X = vfun(interval[:,None], pivots, truths)
print(X.shape)     # (300,3)
y2 = np.dot(X, coeffs)
print(y2.shape)    # (300,)

Это делает более полное использование vectorize's вещания.

Я подозреваю, что ваш fun может быть написано так, чтобы действовать в целом xбез итерации vectorize делает.

изменения fun использовать np.maximumПозволяет мне предоставить массив x:

def fun(x, pivot, truth):
    if truth: return np.maximum(0, x - pivot)
    else:     return np.maximum(0, pivot - x)

И я могу тогда рассчитать X только петля над 3 случаями pivots а также truths, подсчитав все interval значения сразу:

X = np.stack([fun(interval, p, t) for p, t in zip(pivots, truths)], axis=-1)
y2 = np.dot(X, coeffs)

другой способ применения 3 "дел"

Xlist = [fun(interval, p, t)*c for p, t, c in zip(pivots, truths, coeffs)]
y2 = np.sum(Xlist, axis=0)

Так как np.dot(..., coeffs) это просто взвешенная сумма. Я не уверен, что это лучше.