Как работают патчи Безье в чайнике в Юте?
Я преждевременно опубликовал кодовое задание по гольфу, чтобы нарисовать чайник Юты, используя этот набор данных ( только чайник). ( Пересмотрено и опубликовано испытание чайника) Но когда я посмотрел на данные глубже, чтобы привести небольшой пример, я понял, что понятия не имею, что происходит с этими данными. Я хорошо понимаю кривые Безье в 2D, реализованные де Кастеляу. Но для 3D это работает так же?
Да! Оно делает!
Данные содержат патчи, содержащие по 16 вершин в каждой. Существует ли стандартный порядок их размещения? И если они соответствуют 2D-кривым, то четыре угловые точки фактически касаются поверхности, а остальные 12 являются элементами управления, верно?
Да!
Мой "первоначальный план" состоял в том, чтобы упростить фигуру прямоугольникам, спроецировать их на холст и нарисовать заполненные фигуры в сером цвете, рассчитанном по величине точечного произведения пятна, нормального к световому вектору. Если я упросту это до сих пор, будет ли он выглядеть как чайник? Нужно ли использовать лучевую трассировку, чтобы получить узнаваемое изображение?
Это субъективно.:-(
Хотя это может выглядеть как несколько вопросов, но все они являются аспектами этого вопроса: "Пожалуйста, Гуру, пожалуйста, научите меня некоторым патчам Безье? Что мне нужно знать, чтобы нарисовать чайник?"
Вот код, который я написал до сих пор. (использует эту матричную библиотеку: mat.ps)
%!
%%BoundingBox: 115 243 493 487
%-115 -243 translate
(mat.ps)run %include matrix library
/tok{ token pop exch pop }def
/s{(,){search{ tok 3 1 roll }{ tok exit }ifelse }loop }def
/f(teapot)(r)file def
/patch[ f token pop { [ f 100 string readline pop s ] } repeat ]def
/vert[ f token pop { [ f 100 string readline pop s ] } repeat ]def
%vert == patch == %test data input
/I3 3 ident def % 3D identity matrix
/Cam [ 0 0 10 ] def % world coords of camera center viewpoint
/Theta [ 0 0 0 ] def % y-rotation x-rotation z-rotation
/Eye [ 0 0 15 ] def % eye relative to camera vp
/Rot I3 def % initial rotation seq
/makerot {
Theta 0 get roty % pan
Theta 1 get rotx matmul % tilt
Theta 2 get rotz matmul % twist
} def
/proj {
Cam {sub} vop % translate to camera coords
Rot matmul % perform camera rotation
0 get aload pop Eye aload pop % extract dot x,y,z and eye xyz
4 3 roll div exch neg % perform perspective projection
4 3 roll add 1 index mul
4 1 roll 3 1 roll sub mul exch % (ez/dz)(dx-ex) (ez/dz)(dy-ey)
} def
/R 20 def
/H -3 def
/ang 0 def
{
300 700 translate
1 70 dup dup scale div setlinewidth
/Cam [ ang sin R mul H ang cos R mul ] def % camera revolves around Y axis at height H, dist R
/Theta [ ang H R atan 0 ] def % rotate camera back to origin
/Rot makerot def % squash rotation sequence into a matrix
patch {
% Four corners
%[ exch dup 0 get exch dup 3 get exch dup 12 get exch 15 get ]
% Boundary curves
[ exch
dup 8 get exch dup 4 get exch dup 0 get exch %curveto4
dup 14 get exch dup 13 get exch dup 12 get exch %curveto3
dup 7 get exch dup 11 get exch dup 15 get exch %curveto2
dup 1 get exch dup 2 get exch dup 3 get exch %curveto1
dup 0 get exch %moveto
pop ]
{ 1 sub vert exch get proj } forall
moveto
curveto curveto curveto curveto
stroke
%flushpage flush (%lineedit)(r)file pop
} forall
pstack
showpage
%exit
/ang ang 10 add def
} loop
Вот оригинальный набор данных Newell Teapot.
И вот мой потрясающе плохой образ: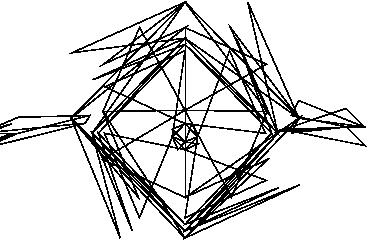
Обновление: исправление. Может быть, они выложены "нормально" в конце концов. Выбор правильных углов, по крайней мере, дает симметричную форму: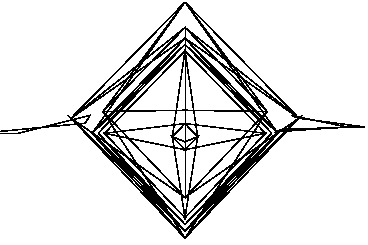
Обновление: граничные кривые выглядят лучше.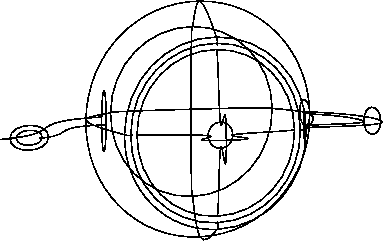
2 ответа
Поверхностный пластырь Bi-Cubic Bezier представляет собой массив трехмерных точек 4x4. Да, четыре угла касаются поверхности; а строки - это кривые Безье, а столбцы - также кривые Безье. Но алгоритм деКастеляу основан на расчете медианы между двумя точками, и в 3D имеет такое же значение, как и в 2D.
Следующим шагом в завершении вышеприведенного кода является подразделение патчей на меньшие части. Тогда извлечение простой граничной кривой выше становится подходящей многоугольной сеткой.
Начните с выравнивания патчей, вставляя данные вершин напрямую, а не используя отдельный кеш. Этот код перебирает патчи, ищет точки в массиве вершин и создает новый массив патчей, который затем переопределяется с тем же именем.
/patch[ patch{ [exch { 1 sub vert exch get }forall ] }forall ]def
Тогда нам понадобится алгоритм деКастеляу, чтобы разбить кривые Безье. vop происходит из библиотеки матриц и применяет двоичную операцию к соответствующим элементам вектора и в результате создает новый вектор.
/median { % [x0 y0 z0] [x1 y1 z1]
{add 2 div} vop % [ (x0+x1)/2 (y0+y1)/2 (z0+z1)/2 ]
} def
/decasteljau { % [P0] P1 P2 P3 . P0 P1' P2' P3' P3' P4' P5' P3
{p3 p2 p1 p0}{exch def}forall
/p01 p0 p1 median def
/p12 p1 p2 median def
/p23 p2 p3 median def
/p012 p01 p12 median def
/p123 p12 p23 median def
/p0123 p012 p123 median def
p0 p01 p012 p0123 % first half-curve
p0123 p123 p23 p3 % second half-curve
} def
Затем некоторые манипуляции со стеком применяются к каждому ряду патча и объединяют результаты в 2 новых патча.
/splitrows { % [b0 .. b15] . [c0 .. c15] [d0 .. d15]
aload pop % b0 .. b15
4 { % on each of 4 rows
16 12 roll decasteljau % roll the first 4 to the top
8 4 roll % exch left and right halves (probably unnecessary)
20 4 roll % roll new curve to below the patch (pushing earlier ones lower)
} repeat
16 array astore % pack the left patch
17 1 roll 16 array astore % roll, pack the right patch
} def
Уродливая утилита позволяет нам повторно использовать код строки для столбцов. Комментарии стека были необходимы для написания этой процедуры, поэтому они, вероятно, необходимы для ее прочтения. n j roll бросает n элементов (влево), j раз; == верхние j элементов над n-м элементом (считая от 1). Таким образом, n устойчиво уменьшается, выбирая, куда поместить элемент, а j выбирает, какой элемент поместить туда (перетаскивая все остальное с ним). Если bind Эта процедура будет существенно быстрее, чем процедура на основе словаря.
% [ 0 1 2 3
% 4 5 6 7
% 8 9 10 11
% 12 13 14 15 ]
/xpose {
aload pop % 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
15 12 roll % 0 4 5 6 7 8 9 10 11 12 13 14 15 1 2 3
14 11 roll % 0 4 8 9 10 11 12 13 14 15 1 2 3 5 6 7
13 10 roll % 0 4 8 12 13 14 15 1 2 3 5 6 7 9 10 11
12 9 roll % 0 4 8 12 1 2 3 5 6 7 9 10 11 13 14 15
11 9 roll % 0 4 8 12 1 5 6 7 9 10 11 13 14 15 2 3
10 8 roll % 0 4 8 12 1 5 9 10 11 13 14 15 2 3 6 7
9 7 roll % 0 4 8 12 1 5 9 13 14 15 2 3 6 7 10 11
8 6 roll % 0 4 8 12 1 5 9 13 2 3 6 7 10 11 14 15
7 6 roll % 0 4 8 12 1 5 9 13 2 6 7 10 11 14 15 3
6 5 roll % 0 4 8 12 1 5 9 13 2 6 10 11 14 15 3 7
5 4 roll % 0 4 8 12 1 5 9 13 2 6 10 14 15 3 7 11
4 3 roll % 0 4 8 12 1 5 9 13 2 6 10 14 3 7 11 15
16 array astore
} def
% [ 0 4 8 12
% 1 5 9 13
% 2 6 10 14
% 3 7 11 15 ]
/splitcols {
xpose
splitrows
xpose
} def
Затем примените эти функции к данным патча. Опять переопределение патча каждый раз.
/patch[ patch{ splitrows }forall ]def
/patch[ patch{ splitrows }forall ]def
/patch[ patch{ splitcols }forall ]def
/patch[ patch{ splitcols }forall ]def
Это дает возможность иметь дело с меньшими фрагментами.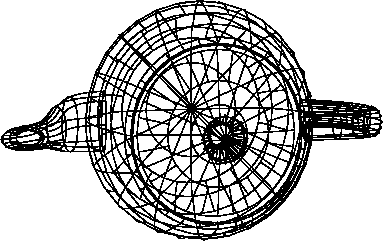
Добавьте тест видимости.
/visible { % patch . patch boolean
dup % p p
dup 3 get exch dup 0 get exch 12 get % p p3 p0 p12
1 index {sub} vop % p p3 p0 v0->12
3 1 roll {sub} vop % p v0->12 v0->3
cross /normal exch def
dup
[ exch dup 0 get exch dup 3 get exch dup 12 get exch 15 get ]
{ Cam {sub} vop normal dot 0 ge } forall
%add add add 4 div 0 lt
or or or
} def
производства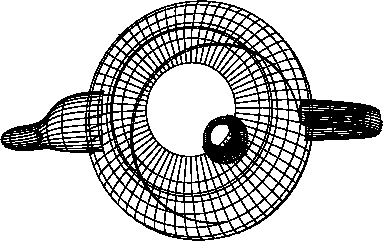
Обновление: тест был задом наперед.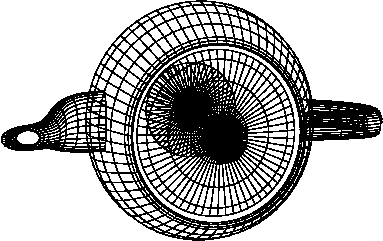
Обновление: тест бесполезен! Из изображения видно, что нижняя часть не ориентирована наружу, и, конечно, отбраковка задней поверхности не препятствует прохождению ручки через горшок. Это требует удаления скрытой поверхности. И так как Postscript не поддерживает Z-буфер, я думаю, это будет раздел двоичного пространства. Так что я вернулась к книгам для меня.
Обновление: добавьте трансформацию Модель-> Мир, чтобы перевернуть предмет.
/Model -90 rotx def % model->world transform
/proj {
Model matmul 0 get % perform model->world transform
Cam {sub} vop % translate to camera coords
...
Производить это.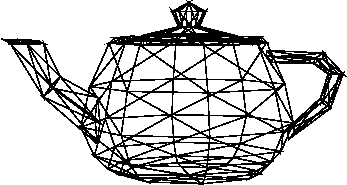
Завершите программу до сих пор. (использует матричную библиотеку: mat.ps.) В ghostscript вы можете просмотреть анимированный поворот, удерживая [enter],
%!
%%BoundingBox: 109 246 492 487
%-109 -246 translate
(mat.ps)run %include matrix library
(det.ps)run %supplementary determinant function
/tok{ token pop exch pop }def
/s{(,){search{ tok 3 1 roll }{ tok exit }ifelse }loop }def
/f(teapot)(r)file def
/patch[ f token pop { [ f 100 string readline pop s ] } repeat ]def
/vert[ f token pop { [ f 100 string readline pop s ] } repeat ]def
/patch[ patch{ [exch { 1 sub vert exch get }forall ] }forall ]def
%vert == patch == %test data input flush quit
/I3 3 ident def % 3D identity matrix
/Cam [ 0 0 10 ] def % world coords of camera center viewpoint
/Theta [ 0 0 0 ] def % y-rotation x-rotation z-rotation
/Eye [ 0 0 15 ] def % eye relative to camera vp
/Rot I3 def % initial rotation seq
/Model -90 rotx def % model->world transform
/makerot {
Theta 0 get roty % pan
Theta 1 get rotx matmul % tilt
Theta 2 get rotz matmul % twist
} def
/proj {
Model matmul 0 get % perform model->world transform
Cam {sub} vop % translate to camera coords
Rot matmul % perform camera rotation
0 get aload pop Eye aload pop % extract dot x,y,z and eye xyz
4 3 roll div exch neg % perform perspective projection
4 3 roll add 1 index mul
4 1 roll 3 1 roll sub mul exch % (ez/dz)(dx-ex) (ez/dz)(dy-ey)
} def
/median { % [x0 y0 z0] [x1 y1 z1]
{add 2 div} vop % [ (x0+x1)/2 (y0+y1)/2 (z0+z1)/2 ]
} def
/decasteljau { % [P0] P1 P2 P3 . P0 P1' P2' P3' P3' P4' P5' P3
{p3 p2 p1 p0}{exch def}forall
/p01 p0 p1 median def
/p12 p1 p2 median def
/p23 p2 p3 median def
/p012 p01 p12 median def
/p123 p12 p23 median def
/p0123 p012 p123 median def
p0 p01 p012 p0123
p0123 p123 p23 p3
} def
/splitrows { % [b0 .. b15] . [c0 .. c15] [d0 .. d15]
aload pop % b0 .. b15
4 {
16 12 roll decasteljau
%8 4 roll
20 4 roll
} repeat
16 array astore
17 1 roll 16 array astore
} def
/xpose {
aload pop % 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
15 12 roll % 0 4 5 6 7 8 9 10 11 12 13 14 15 1 2 3
14 11 roll % 0 4 8 9 10 11 12 13 14 15 1 2 3 5 6 7
13 10 roll % 0 4 8 12 13 14 15 1 2 3 5 6 7 9 10 11
12 9 roll % 0 4 8 12 1 2 3 5 6 7 9 10 11 13 14 15
11 9 roll % 0 4 8 12 1 5 6 7 9 10 11 13 14 15 2 3
10 8 roll % 0 4 8 12 1 5 9 10 11 13 14 15 2 3 6 7
9 7 roll % 0 4 8 12 1 5 9 13 14 15 2 3 6 7 10 11
8 6 roll % 0 4 8 12 1 5 9 13 2 3 6 7 10 11 14 15
7 6 roll % 0 4 8 12 1 5 9 13 2 6 7 10 11 14 15 3
6 5 roll % 0 4 8 12 1 5 9 13 2 6 10 11 14 15 3 7
5 4 roll % 0 4 8 12 1 5 9 13 2 6 10 14 15 3 7 11
4 3 roll % 0 4 8 12 1 5 9 13 2 6 10 14 3 7 11 14
16 array astore
} def
/splitcols {
xpose
splitrows
xpose exch xpose
} def
/patch[ patch{ splitrows }forall ]def
/patch[ patch{ splitrows }forall ]def
/patch[ patch{ splitrows }forall ]def
/patch[ patch{ splitrows }forall ]def
/patch[ patch{ splitcols }forall ]def
/patch[ patch{ splitcols }forall ]def
/color {normal light dot 1 add 4 div
%1 exch sub
setgray} def
/visible { % patch . patch boolean
dup % p p
dup 3 get exch dup 0 get exch 12 get % p p3 p0 p12
1 index {sub} vop % p p3 p0 v0->12
3 1 roll {sub} vop % p v0->12 v0->3
cross /normal exch def
dup
[ exch dup 0 get exch dup 3 get exch dup 12 get exch 15 get ]
{ Cam {sub} vop normal dot 0 ge } forall
%add add add 4 div 0 lt
or or or
} def
/drawpatch {
% Four corners
%[ exch dup 0 get exch dup 3 get exch dup 12 get exch 15 get ]
visible {
[ exch
% control rows
%dup 4 get exch dup 5 get exch dup 6 get exch dup 7 get exch
%dup 11 get exch dup 10 get exch dup 9 get exch dup 8 get exch
% control columns
%dup 1 get exch dup 5 get exch dup 9 get exch dup 13 get exch
%dup 14 get exch dup 10 get exch dup 6 get exch dup 2 get exch
% Boundary curves
dup 8 get exch dup 4 get exch dup 0 get exch %curveto4
dup 14 get exch dup 13 get exch dup 12 get exch %curveto3
dup 7 get exch dup 11 get exch dup 15 get exch %curveto2
dup 1 get exch dup 2 get exch dup 3 get exch %curveto1
dup 0 get exch %moveto
pop ]
{ proj } forall
moveto curveto curveto curveto curveto
%moveto lineto lineto lineto lineto lineto lineto lineto closepath
%moveto lineto lineto lineto lineto lineto lineto lineto closepath
stroke
%flushpage flush (%lineedit)(r)file pop
}{
pop
}ifelse
} def
/R 20 def
/H -3 def
/ang 10 def
{
300 700 translate
1 70 dup dup scale div setlinewidth
% camera revolves around Y axis at height H, dist R
/Cam [ ang sin R mul H ang cos R mul ] def
/Theta [ ang H R atan 0 ] def % rotate camera back to origin
/Rot makerot def % squash rotation sequence into a matrix
patch {
drawpatch
} forall
pstack
showpage
%exit
/ang ang 10 add def
} loop
Основываясь на помощи по математике. StackExchange, меня привели к подзадаче дополнить матричную библиотеку функцией для вычисления определителей.
Итак, этот код проходит некоторые неуклюжие начальные тесты, но он чертовски уродлив, должен признать:
GS>[[1 0][0 1]] det
GS<1>=
1
GS>[[0 1][1 0]] det =
-1
GS>(mat.ps) run
GS>3 ident
GS<1>det =
1
GS>[[1 2 3][4 5 6][7 8 9]] det =
0
GS>
Обновить. Чуть более читабельным.
Обновить. Гораздо удобнее читать, используя точки и крестики. Еще раз спасибо, MvG.
(mat.ps) run % use dot and cross from matrix library
/elem { % M i j
3 1 roll get exch get % M_i_j
} def
/det {
dup length 1 index 0 get length ne { /det cvx /typecheck signalerror } if
1 dict begin /M exch def
M length 2 eq {
M 0 0 elem
M 1 1 elem mul
M 0 1 elem
M 1 0 elem mul sub
}{
M length 3 eq {
M aload pop cross dot
}{ /det cvx /rangecheck signalerror } ifelse
} ifelse
end
} def