Подгонка Гаусса к конкретным данным (Поиск параметров модели)
52.3210481666667 52.3841781666667 52.4938248333333 52.6234071666667 52.9058301666667 53.2846095000000 53.8162295000000 54.4442056666667 55.2349903333333 56.0556786666667 56.9660778333333 57.8731546666667 58.7802311666667 59.6142101666667 60.4249306666667 61.1559080000000 61.7971748333333 62.3387626666667 62.8205433333333 63.2259036666667 63.4950361666667 63.7807816666667 63.9203320000000 64.0964311666667 64.1794968333334 64.2625625000000 64.3323375000000 64.3888223333333 64.5117591666667 64.5017913333333 64.6147606666667 64.6878583333334 64.7476660000000 64.8307311666667 64.9038291666667 65.0334115000000 65.1131545000000 65.2261236666667 65.2792856666667 65.3789643333333 65.4387716666667 65.5052241666667 65.5417731666667 65.5949351666667 65.6248388333333 65.6181933333333 65.6580648333333 65.6181935000000 65.6115481666667 65.5716766666667 65.4985790000000 65.4321263333333 65.3291250000000 65.2394141666667 65.1065091666667 64.9470231666667 64.7709240000000 64.5715665000000 64.3622411666667 64.0764953333333 63.7342651666667 63.3920346666667 62.9899973333333 62.6078951666667 62.1460503333333 61.7207541666667 61.2987811666667 60.9166793333333 60.5478676666667 60.2355410000000 59.9398273333333 59.7703733333333 59.5809840000000 59.5112088333333 59.4281431666667 59.3949168333333 59.4015621666667 59.3616906666667 59.3683361666667 59.3749811666667 59.3384323333333 59.2786250000000 59.2088498333333 59.0825901666667 59.0194603333333 58.8998458333333 58.7270695000000 58.5875188333333 58.4213878333333 58.2619016666667 58.1123836666667 57.9263165000000 57.7535401666667 57.6239576666667 57.4644718333333 57.3382118333333 57.1886940000000 57.0757245000000 56.9162386666667 56.8032695000000 56.6869775000000 56.5540725000000 56.4278128333333 56.3381018333333 56.1885838333333 56.1354216666667 56.0025168333333 55.9493546666667 55.8330628333333 55.7666103333333 55.6835448333333 55.6337053333333 55.5008003333333 55.4509610000000 55.3778633333333 55.2748616666667 55.2117321666667 55.1519248333333 55.0688591666667 54.9990840000000 54.9060503333333 54.8462431666667 54.7731455000000 54.6767891666667 54.6003690000000 54.5239486666667 54.4309151666667 54.3711078333333 54.2946873333333 54.1883635000000 54.1352015000000 54.0454905000000 53.9458116666667 53.9059403333333 53.8261973333333 53.7464543333333 53.6932923333333 53.6069041666667 53.5504195000000 53.5437741666667 53.4308048333333 53.3510618333333 53.3045453333333 53.2646738333333 53.1882535000000 53.1184781666667 53.0752840000000 53.0453805000000 52.9756055000000 52.9091530000000 52.8726038333333 52.8227646666667 52.7563121666667 52.7064725000000 52.6699238333333 52.5802131666667 52.5835355000000 52.5037928333333 52.4572760000000 52.4107590000000 52.3675648333333 52.3144033333333 52.2811766666667 52.2512731666667 52.2114015000000 52.1682075000000 52.1482715000000 52.1283358333333 52.1150456666667 52.0353025000000 52.0353025000000 52.0186893333333 51.9489141666667
Из верхних данных я хочу извлечь формулу гауссовской функции. Формула гауссовой функции y=A*exp(-(x-τ)^2/σ^2) (A - амплитуда, τ - фаза, σ - ширина). Из верхних данных я знаю, что А - 13,7092 (максимальное значение), а τ - 47. Однако я не знаю σ. Я уже рассчитываю σ как стандартное отклонение. Но значение не подходит. Есть ли какая-либо функция в Matlab для извлечения формулы функции? Как я могу решить эту проблему?
2 ответа
Matlab имеет встроенную функцию:
[mu,sigma] = normfit(data)
Но я не понимаю, почему вы думаете, что это гауссово распределение - посмотрите на гистограмму:
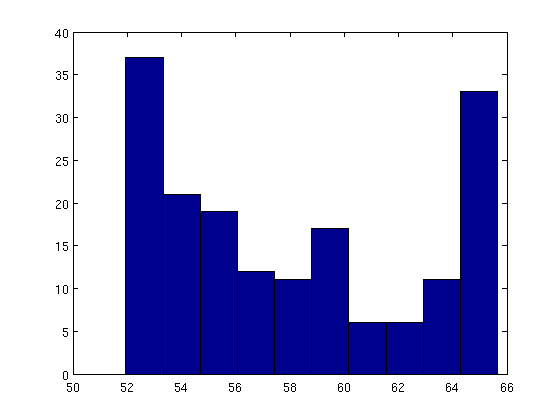
Преобразуйте гауссову функцию, используя натуральный логарифм, в линейное уравнение. Найдите решение наименьших квадратов с помощью mldivide.
bb = (T-x).^2;
AA = log(y)-log(A);
xx = AA\bb;
sprintf('%f',sqrt(abs(xx)))