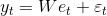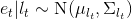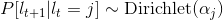Многомерная эмиссионная скрытая марковская модель в STAN

Question

Я пытаюсь реализовать HMM, где наблюдения - это выбросы из HMM первого порядка, свернутые с вейвлетом.

То есть:

С:

а также

Код, который я имею до сих пор, следующий за одномерным случаем, изложенным здесь:

%%writefile HMM_code.stan
data {
int<lower=1> T; // number of observations (length)
int<lower=1> K; // number of hidden states
int<lower=1> H; // number of elements in wavelet vector
vector[K] dir_alpha;
real y[T]; // observations
matrix[T,H] W; // Wavelet matrix
cov_matrix[H] I; //prior covariance
}

parameters {
    // Discrete state model
    simplex[K] pi1; // initial state probabilities
    simplex[K] A[K]; // transition probabilities
    // A[i][j] = p(z_t = j | z_{t-1} = i)
    // Continuous observation model
    vector[H] Mu[K]; // observation means
    real<lower=0> sigma; // observation standard deviations
    cov_matrix[H] Sigma[K]; 
    vector[T] eei[H]; // 
}

transformed parameters {
    vector[K] logalpha[T];
    { // Forward algorithm log p(z_t = j | y_{1:t})
        real accumulator[K];
        logalpha[1] = log(pi1) + multi_normal_lpdf(eei[1] | Mu[][1], Sigma[][1]);
        for (t in 2:T) {
            for (j in 1:K) { // j = current (t)
                for (i in 1:K) { // i = previous (t-1)
                    // Murphy (2012) p. 609 eq. 17.48
                    // belief state + transition prob + local evidence at t
                    accumulator[i] = logalpha[t-1, i] + log(A[i, j]) + multi_normal_lpdf(eei[t] | Mu[][j], Sigma[][i]);
                }
                logalpha[t, j] = log_sum_exp(accumulator);
            }
        }
    } // Forward
}

model{
    Mu ~ multi_normal(rep_vector(0.0,H),I);
    sigma ~ inv_gamma(.1,.1);
    for(k in 1:K)
        A[k] ~ dirichlet(dir_alpha);
    for( j in 1:K)
        Sigma[j] ~ inv_wishart(3.0, I); //Relevant part for this post

    for (t in 1:T)
        y[t] ~ normal(W[t,]*eei[t], pow(sigma,.5));// Likelihood 
}

generated quantities {
    vector[K] alpha[T];
    vector[K] beta[T];
    vector[K] gamma[T];
    vector[K] loggamma[T];
    int<lower=1, upper=K> zstar[T];
    { // Forward algortihm
    for (t in 1:T)
        alpha[t] = softmax(logalpha[t]);
    } // Forward
    { // Backward algorithm log p(eei_{t+1:T} | z_t = j)
        real accumulator[K];
        vector[K] logbeta[T];
        for (j in 1:K)
            logbeta[T, j] = 1;
        for (tforward in 0:(T-2)) {
            int t;
            t = T - tforward;
            for (j in 1:K) { // j = previous (t-1)
                for (i in 1:K) { // i = next (t)
                    // Murphy (2012) Eq. 17.58
                    // backwards t + transition prob + local evidence at t
                    accumulator[i] = logbeta[t, i] + log(A[j, i]) + multi_normal_lpdf(eei[t] | Mu[][i], Sigma[][i]);
                }
                logbeta[t-1, j] = log_sum_exp(accumulator);
            }
        }
        for (t in 1:T)
            beta[t] = softmax(logbeta[t]);
    } // Backward
    { // forward-backward algorithm log p(z_t = j | eei_{1:T})
    for(t in 1:T) {
        loggamma[t] = alpha[t] .* beta[t];
    }
    for(t in 1:T)
        gamma[t] = softmax(loggamma[t]);
    } // forward-backward
    { // Viterbi algorithm
        real logp_zstar;
        int bpointer[T, K]; // backpointer to the most likely previous state on the most probable path
        real delta[T, K]; // max prob for the sequence up to t
        // that ends with an emission from state k
        for (j in 1:K)
            delta[1, K] = multi_normal_lpdf(eei[1] | Mu[][j], Sigma[][j]);
        for (t in 2:T) {
            for (j in 1:K) { // j = current (t)
                delta[t, j] = negative_infinity();
                for (i in 1:K) { // i = previous (t-1)
                    real logp;
                    logp = delta[t-1, i] + log(A[i, j]) + multi_normal_lpdf(eei[t] | Mu[][i], Sigma[][i]);
                    if (logp > delta[t, j]) {
                        bpointer[t, j] = i;
                        delta[t, j] = logp;
                    }
                }
            }
        }
        logp_zstar = max(delta[T]);
        for (j in 1:K)
            if (delta[T, j] == logp_zstar)
                zstar[T] = j;
        for (t in 1:(T - 1)) {
            zstar[T - t] = bpointer[T - t + 1, zstar[T - t + 1]];
        }
    }
}

Скомпилировано с использованием:

%%time
sm = pystan.StanModel(file='HMM_code.stan')

И подходит с помощью:

%%time
fit = sm.sampling(data=HMM_data, iter=1, thin = 1, verbose = True)

Ошибка, которую я получаю, находится в первой строке при оценке функции multi_normal_pdf, говоря, что "LDLT_Factor параметра ковариации не является положительно определенным. Последняя условная дисперсия составляет 2.77556e-16"

Answer 1

Большие ковариационные матрицы легко могут быть численно сингулярными, даже в этом случае, когда они положительно определены по построению. Чтобы избежать этой проблемы и ненужных вычислений, в Stan обычно нужно объявить параметр как коэффициент Холецкого ковариационной или корреляционной матрицы (в этом случае вам также нужно объявить положительный вектор стандартных отклонений в параметрах). блок).

В этом случае вы бы назвали multi_normal_cholesky_lpdf функция, которая обусловливает фактор Холецкого ковариационной матрицы, а не саму ковариационную матрицу, которая, в свою очередь, может быть diag_pre_multiply вектора стандартных отклонений и коэффициент Холецкого корреляционной матрицы. Тем не менее, в этом случае вам нужно будет переключить приоры с обратного Wishart на lkj_corr_cholesky_lpdf для коэффициента Холецкого матрицы корреляции и все, что вы хотите (например, exponential_lpdf) для стандартных отклонений. Все это обсуждается в руководстве пользователя Stan.

Другой вариант - интегрировать ковариационные матрицы.