Сравнивая все переменные в функции ПЦР из пакета pls, R

Question

Я пытаюсь провести регрессионный анализ главных компонентов (PCR) в R. Обычно я делаю PCA (анализ основных компонентов), однако у меня есть мультиколлинеарность и я прочитал, что PCR может справиться с этим.

Я использую pcrфункция от pls пакет. Это требует формулы для определения переменных для сравнения. Я хочу иметь возможность сравнивать каждую переменную с любой другой переменной, как это делает PCA. Однако в этой функции я могу только выяснить, как сравнить одну переменную с любой другой переменной, и в зависимости от того, какую переменную я выберу, результат меняется. Конечно, возможно, я не правильно понимаю ПЦР.

Вот пример использования iris набор данных.

library(pls)
library(ggplot2)

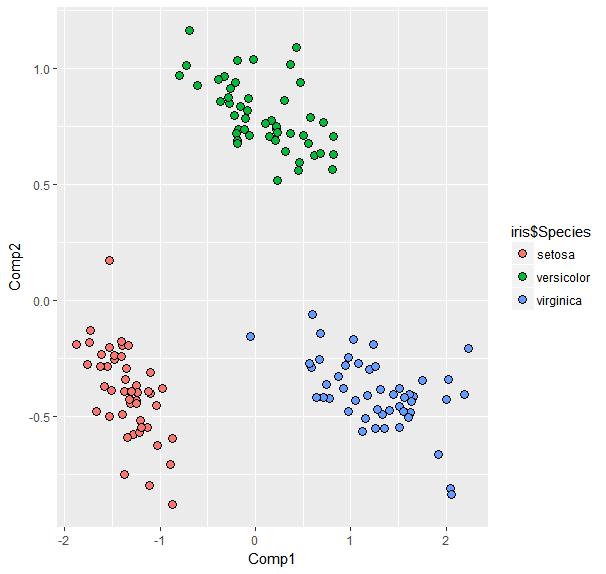
Сравнение Petal.Length для всех остальных переменных:

ir.pcr<-pcr(Petal.Length~ ., data = iris, validation = "CV")#PCR comparing `Petal.Length` with all other variables

df<-data.frame(ir.pcr$scores[,1],ir.pcr$scores[,2])#get first 2 COMP scores from PCR for ggplot
colnames(df)<-c('Comp1', 'Comp2')

ggplot(data=df,aes(x=Comp1,y=Comp2)) + 
  geom_point(aes(fill=iris$Species),shape=21,colour='black',size=3)#plot points

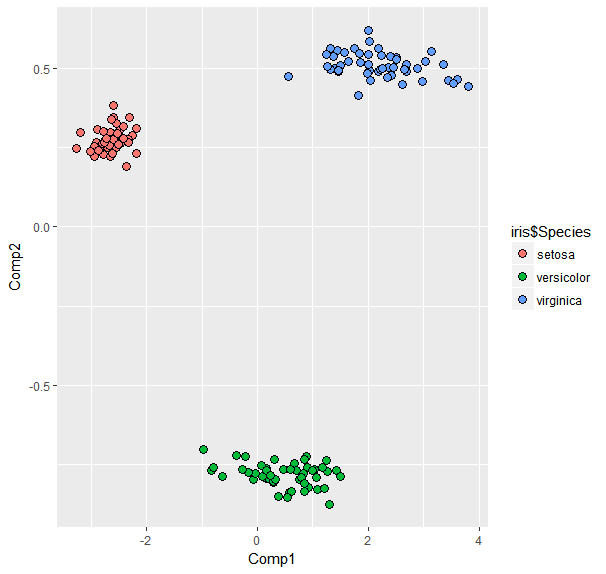
С помощью Sepal.Width по сравнению с любой другой переменной:

ir.pcr<-pcr(Sepal.Width~ ., data = iris, validation = "CV")#PCR

df<-data.frame(ir.pcr$scores[,1],ir.pcr$scores[,2])#get first 2 COMP scores from PCR for ggplot
colnames(df)<-c('Comp1', 'Comp2')

ggplot(data=df,aes(x=Comp1,y=Comp2)) + 
  geom_point(aes(fill=iris$Species),shape=21,colour='black',size=3)#plot points

Я понимаю, что в том числе . после ~ в формуле означает "сравнить со всем остальным". Если это так, то как я могу по существу иметь .~. чтобы иметь возможность сравнить каждую переменную с любой другой переменной?

Answer 1

ПЦР является основным компонентом регрессии. Это означает, что у вас есть одна зависимая переменная (в левой части ~) и множество независимых переменных (правая часть ~) прямо как в линейной регрессии.

Сначала ПЦР проводит PCA только по независимым переменным, а затем регрессирует зависимую переменную по основным компонентам из PCA. Вот почему вы получаете разные результаты при выборе разных зависимых переменных.

Это помогает иметь дело с мультиколлинеарностью только независимых переменных. Так что этот метод полезен, когда вы хотите запустить линейную регрессию, но у вас есть проблема мультиколлинеарности с независимыми переменными. Это бесполезно в задаче сокращения измерений (например, когда у вас нет указанной зависимой переменной), как PCA.