Создать массив случайных целых чисел с неравномерным распределением
Я хочу написать код Java для создания массива случайных целых чисел в диапазоне [1,4]. Длина массива равна N, что указывается во время выполнения. Проблема в том, что диапазон [1,4] не распределен равномерно:
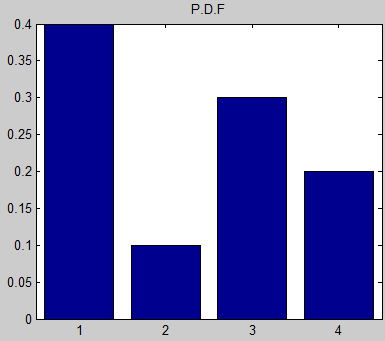
Это означает, что если я создаю массивы с N=100, число "1" будет появляться в массиве в среднем 40 раз, число "2" - 10 раз и т. Д.
Сейчас я использую этот код для генерации равномерно распределенных случайных чисел в диапазоне [1,4]:
public static void main(String[] args)
{
int N;
System.out.println();
System.out.print("Enter an integer number: ");
N = input.nextInt();
int[] a = new int[N];
Random generator = new Random();
for(int i = 0; i < a.length; i++)
{
a[i] = generator.nextInt(4)+1;
}
}
Как мне реализовать это с неравномерным распределением, как показано на графике выше?
6 ответов
Вот способ сделать это, начиная с вашего кода:
public static void main(String[] args){
int N;
System.out.println();
System.out.print("Enter an integer number: ");
N = input.nextInt();
int[] a = new int[N];
Random generator = new Random();
for (int i = 0; i < a.length; i++) {
float n = generator.nextFloat();
if (n <= 0.4) {
a[i] = 1;
} else if (n <= 0.7) {
a[i] = 3;
} else if (n <= 0.9) {
a[i] = 4;
} else {
a[i] = 2;
}
}
}
ОБНОВЛЕНИЕ: по предложению @pjs выберите числа в порядке вероятности снижения, чтобы вы могли выйти из блока if раньше
Другое простое решение - использовать nextDouble(), который генерирует случайный дубль в [0,1). Если значение <.4, выберите 1, иначе, если оно <(.4 +.2), выберите 2 и т. Д., Причем последняя ветвь всегда выбирает последний выбор. Это легко обобщается с помощью цикла for.
Для более общего подхода вы можете заполнить NavigableMap с вероятностью распределения:
double[] probs = {0.4, 0.1, 0.2, 0.3};
NavigableMap<Double, Integer> distribution = new TreeMap<Double, Integer>();
for(double p : probs) {
distribution.put(distribution.isEmpty() ? p : distribution.lastKey() + p, distribution.size() + 1);
}
и позже запросите карту с равномерно распределенным случайным ключом в диапазоне [0, 1>:
Random rnd = new Random();
for(int i=0; i<20; i++) {
System.out.println(distribution.ceilingEntry(rnd.nextDouble()).getValue());
}
Это заполнит карту следующими парами ключ / значение:
0.4 -> 1
0.5 -> 2
0.7 -> 3
1.0 -> 4
Чтобы запросить карту, сначала необходимо сгенерировать равномерно распределенный дубль в диапазоне от 0 до 1. Запросить карту с помощью ceilingEntry метод и передача случайного числа вернут "отображение, связанное с наименьшим ключом, большим или равным данному ключу", поэтому, например, передача значения в диапазоне <0,4, 0,5] вернет запись с отображением 0.5 -> 2, С помощью getValue() на возвращенной карте запись, следовательно, вернет 2.
Для конкретной проблемы, которую вы указали выше, решения, предоставленные другими, работают очень хорошо, и метод псевдонимов будет излишним. Тем не менее, вы сказали в комментарии, что вы собираетесь использовать это в дистрибутиве с гораздо большим диапазоном. В этом случае может потребоваться дополнительная установка таблицы псевдонимов для получения поведения O(1) для фактической генерации значений.
Вот источник на Java. Легко вернуть его обратно к использованию акций Java Random если вы не хотите взять Мерсенна Твистера:
/*
* Created on Mar 12, 2007
* Feb 13, 2011: Updated to use Mersenne Twister - pjs
*/
package edu.nps.or.simutils;
import java.lang.IllegalArgumentException;
import java.text.DecimalFormat;
import java.util.Comparator;
import java.util.Stack;
import java.util.PriorityQueue;
import java.util.Random;
import net.goui.util.MTRandom;
public class AliasTable<V> {
private static Random r = new MTRandom();
private static DecimalFormat df2 = new DecimalFormat(" 0.00;-0.00");
private V[] primary;
private V[] alias;
private double[] primaryP;
private double[] primaryPgivenCol;
private static boolean notCloseEnough(double target, double value) {
return Math.abs(target - value) > 1E-10;
}
/**
* Constructs the AliasTable given the set of values
* and corresponding probabilities.
* @param value
* An array of the set of outcome values for the distribution.
* @param pOfValue
* An array of corresponding probabilities for each outcome.
* @throws IllegalArgumentException
* The values and probability arrays must be of the same length,
* the probabilities must all be positive, and they must sum to one.
*/
public AliasTable(V[] value, double[] pOfValue) {
super();
if (value.length != pOfValue.length) {
throw new IllegalArgumentException(
"Args to AliasTable must be vectors of the same length.");
}
double total = 0.0;
for (double d : pOfValue) {
if (d < 0) {
throw new
IllegalArgumentException("p_values must all be positive.");
}
total += d;
}
if (notCloseEnough(1.0, total)) {
throw new IllegalArgumentException("p_values must sum to 1.0");
}
// Done with the safety checks, now let's do the work...
// Cloning the values prevents people from changing outcomes
// after the fact.
primary = value.clone();
alias = value.clone();
primaryP = pOfValue.clone();
primaryPgivenCol = new double[primary.length];
for (int i = 0; i < primaryPgivenCol.length; ++i) {
primaryPgivenCol[i] = 1.0;
}
double equiProb = 1.0 / primary.length;
/*
* Internal classes are UGLY!!!!
* We're what you call experts. Don't try this at home!
*/
class pComparator implements Comparator<Integer> {
public int compare(Integer i1, Integer i2) {
return primaryP[i1] < primaryP[i2] ? -1 : 1;
}
}
PriorityQueue<Integer> deficitSet =
new PriorityQueue<Integer>(primary.length, new pComparator());
Stack<Integer> surplusSet = new Stack<Integer>();
// initial allocation of values to deficit/surplus sets
for (int i = 0; i < primary.length; ++i) {
if (notCloseEnough(equiProb, primaryP[i])) {
if (primaryP[i] < equiProb) {
deficitSet.add(i);
} else {
surplusSet.add(i);
}
}
}
/*
* Pull the largest deficit element from what remains. Grab as
* much probability as you need from a surplus element. Re-allocate
* the surplus element based on the amount of probability taken from
* it to the deficit, surplus, or completed set.
*
* Lather, rinse, repeat.
*/
while (!deficitSet.isEmpty()) {
int deficitColumn = deficitSet.poll();
int surplusColumn = surplusSet.pop();
primaryPgivenCol[deficitColumn] = primaryP[deficitColumn] / equiProb;
alias[deficitColumn] = primary[surplusColumn];
primaryP[surplusColumn] -= equiProb - primaryP[deficitColumn];
if (notCloseEnough(equiProb, primaryP[surplusColumn])) {
if (primaryP[surplusColumn] < equiProb) {
deficitSet.add(surplusColumn);
} else {
surplusSet.add(surplusColumn);
}
}
}
}
/**
* Generate a value from the input distribution. The alias table
* does this in O(1) time, regardless of the number of elements in
* the distribution.
* @return
* A value from the specified distribution.
*/
public V generate() {
int column = (int) (primary.length * r.nextDouble());
return r.nextDouble() <= primaryPgivenCol[column] ?
primary[column] : alias[column];
}
public void printAliasTable() {
System.err.println("Primary\t\tprimaryPgivenCol\tAlias");
for(int i = 0; i < primary.length; ++i) {
System.err.println(primary[i] + "\t\t\t"
+ df2.format(primaryPgivenCol[i]) + "\t\t" + alias[i]);
}
System.err.println();
}
}
Позволять a1, a2, a3 а также a4 быть двойниками, которые определяют относительные вероятности и s = a1+a2+a3+a4Это означает вероятность 1 является a1/sвероятность для 2 является a2/s...
Затем создайте случайный двойной d, используя generator.nextDouble(),
Если 0 <= d < a1/s тогда целое число должно быть 1,
если a1/s <= d < (a1+a2)/s тогда целое число должно быть 2
если (a1+a2)/s <= d < (a1+a2+a3)/s тогда целое число должно быть 3
если (a1+a2+a3)/s <= d < 1 тогда целое число должно быть 4
Немного более расширяемая версия Miquel's (а также то, что предложила Тереза):
double[] distro=new double[]{.4,.1,.3,.2};
int N;
System.out.println();
System.out.print("Enter an integer number: ");
Scanner input = new Scanner(System.in);
N = input.nextInt();
int[] a = new int[N];
Random generator = new Random();
outer:
for(int i = 0; i < a.length; i++)
{
double rand=generator.nextDouble();
double val=0;
for(int j=1;j<distro.length;j++){
val+=distro[j-1];
if(rand<val){
a[i]=j;
continue outer;
}
}
a[i]=distro.length;
}