Построение прогнозируемых значений по модели Ime (с полиномами) в R

Question

Я использую линейную модель смешанного эффекта (запустить с lme() функция в пакете nlme в R), которая имеет один фиксированный эффект и один случайный член перехвата (для учета разных групп). Модель представляет собой кубическую полиномиальную модель, указанную так (следуя советам, приведенным ниже):

   M1 = lme(dv ~ poly(iv,3), data=dat, random= ~1|group, method="REML")

Только некоторые примеры данных:

> dput(dat)
structure(list(group = structure(c(1L, 1L, 1L, 1L, 1L, 1L, 1L, 
1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 1L, 
1L, 1L, 1L, 1L, 1L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 
2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L, 2L), .Label = c("1", 
"2"), class = "factor"), iv = c(24L, 100L, 110L, 115L, 116L, 
120L, 125L, 127L, 138L, 139L, 142L, 150L, 152L, 154L, 157L, 161L, 
168L, 177L, 181L, 189L, 190L, 198L, 200L, 213L, 216L, 225L, 254L, 
284L, 40L, 51L, 76L, 130L, 155L, 158L, 160L, 163L, 167L, 169L, 
170L, 177L, 185L, 190L, 203L, 206L, 208L, 219L, 223L, 233L, 238L, 
244L, 251L, 260L, 265L), dv = c(0L, 8L, 6L, 8L, 10L, 10L, 9L, 
11L, 12L, 15L, 16L, 19L, 13L, 10L, 17L, 22L, 18L, 22L, 25L, 20L, 
27L, 28L, 29L, 30L, 29L, 30L, 30L, 30L, 0L, 0L, 2L, 7L, 14L, 
12L, 17L, 10L, 14L, 13L, 16L, 15L, 17L, 21L, 25L, 20L, 26L, 27L, 
28L, 29L, 30L, 30L, 30L, 30L, 30L)), .Names = c("group", "iv", 
"dv"), row.names = c(NA, -53L), class = "data.frame")

Теперь я хотел бы построить подходящие значения, используя predict функция (значения iv не являются непрерывными в наборе данных, поэтому я хотел бы улучшить внешний вид / плавность подгонки кривой).

Используя онлайновые примеры того, как построить прогнозируемые значения из простой модели lme (без полиномов) (см. Здесь: Извлечение полосы прогнозирования из подгонки lme и http://glmm.wikidot.com/faq), я могу построить прогнозируемую "популяцию". 'означает для меня без полиномов, используя следующий код:

#model without polynomials
dat$group = factor(dat$group)
M2 = lme(dv ~ iv, data=dat, random= ~1|group, method="REML")

#1.create new data frame with new values for predictors (where groups aren't accounted for)
range(dat$iv)
new.dat = data.frame(iv = seq(from =24, to =284, by=1))

#2. predict the mean population response
new.dat$pred = predict(M2, newdata=new.dat, level=0)

#3. create a design matrix
Designmat <- model.matrix(eval(eval(M2$call$fixed)[-2]), new.dat[-ncol(new.dat)])

#4. get standard error and CI for predictions
predvar <- diag(Designmat %*% M2$varFix %*% t(Designmat)) 
new.dat$SE <- sqrt(predvar) 
new.dat$SE2 <- sqrt(predvar+M2$sigma^2)

# Create plot with different colours for grouping levels and plot predicted values for population mean
G1 = dat[dat$group==1, ]
G2 = dat[dat$group==2, ]

plot(G1$iv, G1$dv, xlab="iv", ylab="dv", ylim=c(0,30), xlim=c(0,350), pch=16, col=2)
points(G2$iv, G2$dv, xlab="", ylab="", ylim=c(0,30), xlim=c(0,350), pch=16, col=3)

F0 = new.dat$pred
I = order(new.dat$iv); eff = sort(new.dat$iv)
lines(eff, F0[I], lwd=2, type="l", ylab="", xlab="", col=1, xlim=c(0,30))
#lines(eff, F0[I] + 2 * new.dat$SE[I], lty = 2)
#lines(eff, F0[I] - 2 * new.dat$SE[I], lty = 2)

Я хотел бы расширить этот код, чтобы 1) построить прогнозируемые линии внутри группы, а также средние значения населения и 2) определить, как код может быть адаптирован для построения прогнозируемых кривых "население" и "внутри группы" для lme с полиномы (то есть модель M1 выше).

Получение групповых прогнозов: я могу получить один набор прогнозируемых значений для групп, используя приведенный ниже код, но я хотел бы построить линию для каждой группы, а также среднее значение по населению, а в случае данных примера я не вижу, как предсказанные значения для двух групповых строк могут быть извлечены?

new.dat = data.frame(iv = dat$iv, group=rep(c("1","2"),c(28,25)))
Pred = predict(M2, newdata=new.dat, level=0:1)

Кроме того, это не работает, если вы хотите предсказать большее число значений, чем количество исходных значений iv (например, в случае, если у вас есть нерегулярные данные). Очевидно, что приведенное ниже не будет работать из-за различного количества строк, но я борюсь с синтаксисом.

new.dat = data.frame(iv = seq(from =24, to =284, by=1), group=rep(c("1","2"),c(28,25)))

Для полиномиальной модели: я не понимаю, как можно включить poly(iv,3) в фрейм данных new.dat для подачи в функцию прогнозирования.

Любой совет о том, как достичь этих двух целей, был бы очень признателен, так как я пытался понять это некоторое время без радости (я бы предпочел использовать базовую графику, чем ggplot, если это возможно). Спасибо!

Answer 1

Позвольте мне объяснить более подробно, почему я думаю, что вы переходите на нелинейные термины слишком быстро и должны тратить больше времени на изучение ваших данных, прежде чем рассматривать полиномиальные термины:

Первый, более правильный способ ввода полиномиальных членов 2-го и 3-го порядка:

> M1 = lme(dv ~ poly(iv ,3), data=dat, random= ~1|group, method="REML")
> summary(M1)
Linear mixed-effects model fit by REML
 Data: dat 
       AIC      BIC    logLik
  245.4883 256.8393 -116.7442

Random effects:
 Formula: ~1 | group
        (Intercept) Residual
StdDev:    2.465855 2.435135

Fixed effects: dv ~ poly(iv, 3) 
                 Value Std.Error DF   t-value p-value
(Intercept)   18.14854  1.775524 48 10.221507  0.0000
poly(iv, 3)1  64.86375  2.476145 48 26.195452  0.0000
poly(iv, 3)2   2.76606  2.462331 48  1.123349  0.2669
poly(iv, 3)3 -13.90253  2.485106 48 -5.594339  0.0000
 Correlation: 
             (Intr) p(,3)1 p(,3)2
poly(iv, 3)1 -0.002              
poly(iv, 3)2 -0.002  0.027       
poly(iv, 3)3  0.002 -0.036 -0.030

Standardized Within-Group Residuals:
       Min         Q1        Med         Q3        Max 
-2.6349301 -0.6172897  0.1653097  0.7076490  1.6581112 

Number of Observations: 53
Number of Groups: 2 

Теперь, почему кубический термин был бы значимым, если квадратный член не был? Посмотрите на данные... которые должны были быть первым порядком бизнеса, а не последним:

library(lattice)
xyplot( dv ~ iv|group, dat)
png(); print(xyplot( dv ~ iv|group, dat) ); dev.off()

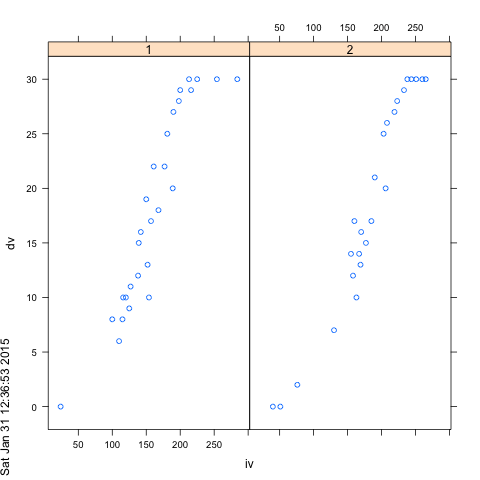
Как становится очевидным при простом вызове построения графиков, их систематическая отсечка в 30 (и, возможно, в 0, хотя там немного немного данных). Таким образом, вы бы приписали потолочный эффект, накладываемый вашими методами измерения, на какой-то нелинейный термин.

Answer 2

Perhaps not exactly the the answer asked for, but the data plotted by @42- looks sigmoidal. In laymans terms it is pretty flat, gets steep, and gets flat again. If that is a good way to interpret the process being studied, maybe it is a better, more explainable model to use than the generic polynomial. It would give more answers about specific features of the process.

A way to fit this type of data with random effects is given in this answer.

Non-linear mixed effects regression in R