Ищите библиотеку C/C++, вычисляющую максимум кривой Гаусса с использованием дискретных значений

Question

У меня есть некоторые дискретные значения и предположение, что эти значения лежат на кривой Гаусса. Должен быть алгоритм для максимального расчета, использующий только 3 дискретных значения. Знаете ли вы какую-либо библиотеку или код в C/C++, реализующий этот расчет?

Спасибо!

PS: оригинальная задача - реализация автофокуса. Я перемещаю (микроскоп) камеру и снимаю фотографии в разных положениях. Позиция, имеющая самые разные цвета, должна иметь лучший фокус.

РЕДАКТИРОВАТЬ Это было давно:-(Я просто хотел удалить этот вопрос, но оставил его, уважая хороший ответ.

Answer 1

У вас есть три точки, которые должны быть на кривой Гаусса; это означает, что они лежат на функции:

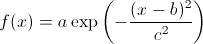
Если вы возьмете логарифм этой функции, вы получите:

который представляет собой простой полином 2-го класса, то есть параболу с вертикальной осью симметрии:

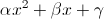
с

Итак, если вы знаете три коэффициента параболы, вы можете получить параметры кривой Гаусса; кстати, единственный параметр гауссовой функции, который представляет для вас определенный интерес, - это b, поскольку он сообщает вам, где находится центр распределения, т.е. где находится его максимум. Это немедленно выяснить, что

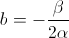
Все, что остается сделать, это подогнать параболу (с "оригинальным" x и логарифмом ваших значений). Теперь, если бы у вас было больше точек, было бы использовано полиномиальное соответствие, но, поскольку у вас есть только три точки, ситуация действительно проста: есть одна и только одна парабола, которая проходит через три точки.

Теперь вам просто нужно написать уравнение параболы для каждой из ваших точек и решить систему:

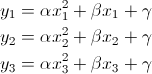
(с 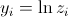где z s - фактические значения, прочитанные в соответствующем x)

Это можно решить вручную (через некоторое время), с помощью некоторого CAS или... глядя на Stackru:); решение таким образом:

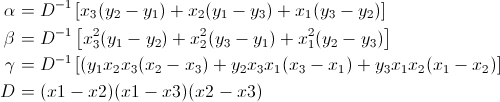
Поэтому, используя эти последние уравнения (помните: y s - это логарифм ваших "реальных" значений) и другие соотношения, вы можете легко написать простую алгебраическую формулу, чтобы получить параметр b вашей гауссовой кривой, то есть ее максимум.

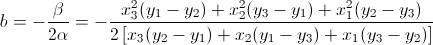
(Я, возможно, сделал некоторые ошибки в вычислениях, перепроверьте их перед использованием результатов, в любом случае процедура должна быть правильной)

(спасибо на http://www.codecogs.com/latex/eqneditor.php за уравнения LaTeX)