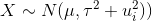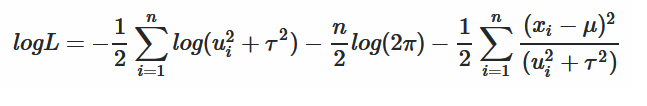Запись правильного нормального логарифмического правдоподобия в R

Question

У меня есть проблема относительно следующей модели,

где я хочу сделать вывод о µ и tau, u - известный вектор, а x - вектор данных. Логарифмическая вероятность

У меня проблема с записью правдоподобия в R.

x <- c(3.3569,1.9247,3.6156,1.8446,2.2196,6.8194,2.0820,4.1293,0.3609,2.6197)
mu <- seq(0,10,length=1000)

normal.lik1<-function(theta,x){ 
  u <- c(1,3,0.5,0.2,2,1.7,0.4,1.2,1.1,0.7)  
  mu<-theta[1] 
  tau<-theta[2] 
  n<-length(x) 

logl <-  sapply(c(mu,tau),function(mu,tau){logl<- -0.5*n*log(2*pi) -0.5*n*log(tau^2+u^2)- (1/(2*tau^2+u^2))*sum((x-mu)^2) } )

  return(logl) 
  } 

#test if it works for mu=1, tau=2
head(normal.lik1(c(1,2),x))
#Does not work..

Я хочу иметь возможность подключить вектор для mu и построить его поверх mu для фиксированного значения tau, скажем 2. Я также хочу узнать MLE для tau и mu, используя функцию optim. Я старался:

theta.hat<-optim(c(1,1),loglike2,control=list(fnscale=-1),x=x,,method="BFGS")$par

Но это не работает.. Любые предложения о том, как я могу написать вероятность?

Answer 1

Во-первых, как уже упоминалось в комментариях к вашему вопросу, нет необходимости использовать sapply(), Вы можете просто использовать sum() - так же, как в формуле журнала.

Я изменил эту часть в normal.lik1() и умножил выражение, которое назначено logl на минус 1, так что функция вычисляет минус logLikelihood. Вы хотите найти минимум сверх тета, так как функция возвращает положительные значения.

x < c(3.3569,1.9247,3.6156,1.8446,2.2196,6.8194,2.0820,4.1293,0.3609,2.6197)
u <- c(1,3,0.5,0.2,2,1.7,0.4,1.2,1.1,0.7) 

normal.lik1 <- function(theta,x,u){ 
  mu <- theta[1] 
  tau <- theta[2] 
  n <- length(x) 
  logl <- - n/2 * log(2*pi) - 1/2 * sum(log(tau^2+u^2)) - 1/2 * sum((x-mu)^2/(tau^2+u^2))
  return(-logl) 
}

Это можно сделать с помощью nlm(), например

nlm(normal.lik1, c(0,1), hessian=TRUE, x=x,u=u)$estimate

где c(0,1) являются начальными значениями для алгоритма.

Чтобы построить logLikelihood для диапазона значений mu и некоторые исправлены tau Вы можете настроить функцию так, чтобы mu а также tau это отдельные числовые аргументы.

normal.lik2 <- function(mu,tau,x,u){ 
  n <- length(x) 
  logl <- - n/2 * log(2*pi) - 1/2 * sum(log(tau^2+u^2)) - 1/2 * sum((x-mu)^2/(tau^2+u^2))
  return(logl) 
}

Затем определите некоторый диапазон для mu, вычислить логарифмическую вероятность и использовать plot(),

range.mu <- seq(-10,20,0.1)

loglik <- sapply(range.mu, function(m) normal.lik2(mu=m,tau=2,x=x,u=u))

plot(range.mu, loglik, type = "l")

Я уверен, что есть более элегантные способы сделать это, но это делает свое дело.