Угол между пересекающимися плоскостями, нарисованными с помощью matplotlib

Question

Мне нужно создать график с пересекающимися плоскостями, подобный представленному в вопросе: Как нарисовать пересекающиеся плоскости?, Принятый ответ на этот вопрос - отличный кусок кода от tacaswell (код ниже).

В этом коде вар angle используется, который, по-видимому, контролирует угол между каждой плоскостью. Для небольших значений это, конечно, ведет себя так, но для больших значений это не так.

Например, это результаты для значений angle = 0.25, 0.5, 1, 5, 50, 100,

Переменная, очевидно, влияет на угол между плоскостями, но она также контролирует расширение наклонной плоскости. Сначала я хоть angles было выражено в радианах, но это не так. Он также не выражен в градусах, как видно на изображении выше, где он никогда не достигает угла 90 ° между плоскостями.

Тогда возникает вопрос: что делает эта переменная? И как я могу контролировать угол между плоскостями?

---

Код:

from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np


fig = plt.figure()
ax = Axes3D(fig)

dim = 10

# Define x,y plane.
X, Y = np.meshgrid([-dim, dim], [-dim, dim])
Z = np.zeros((2, 2))

# Define inclined plane.
angle = 0.5  # <-- This is the variable
X2, Y2 = np.meshgrid([-dim, dim], [0, dim])
Z2 = Y2 * angle
X3, Y3 = np.meshgrid([-dim, dim], [-dim, 0])
Z3 = Y3 * angle

# Plot x,y plane.
ax.plot_surface(X, Y, Z, color='gray', alpha=.5, linewidth=0, zorder=1)
# Plot top half of inclined plane.
ax.plot_surface(X2, Y2, Z2, color='blue', alpha=.5, linewidth=0, zorder=3)
# Plot bottom half of inclined plane.
ax.plot_surface(X2, Y3, Z3, color='blue', alpha=.5, linewidth=0, zorder=-1)

ax.set_xlim(-10., 10.)
ax.set_ylim(-10., 10.)
ax.set_zlim(-10., 10.)
plt.show()

Answer 1

Что вызвано angle это просто множитель для Y-координаты. Таким образом, для малых углов результат одинаков, однако для поворота на 90 градусов коэффициент должен быть равен бесконечности.

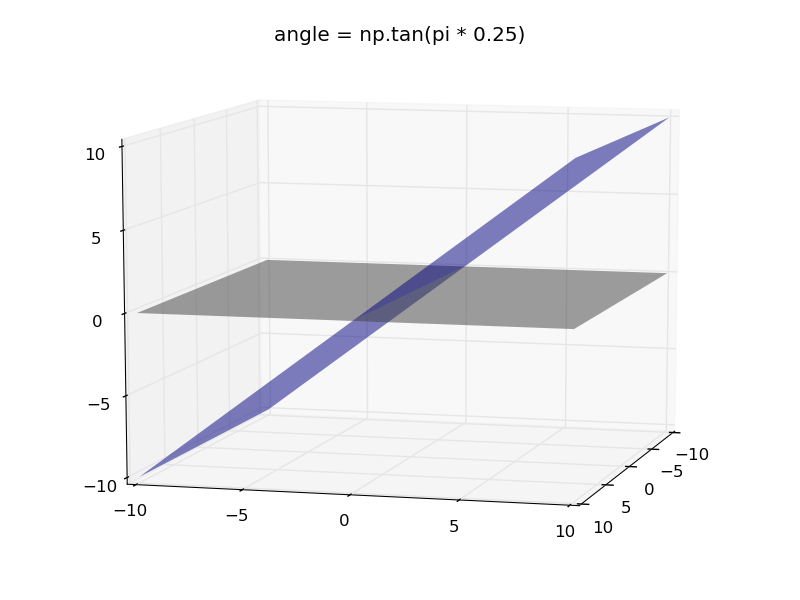
Вы можете переопределить угол, используя tanget и введя данные в радианах:

angle = np.tan(pi * 0.25)

Теперь вы увидите фактическое вращение с указанным углом.

---

более чистая модификация может быть:

# Define inclined plane.
angle = pi * 0.5  # <-- This is the variable
X2, Y2 = np.meshgrid([-dim, dim], [0, dim])
Z2 = Y2 * np.tan(angle)
X3, Y3 = np.meshgrid([-dim, dim], [-dim, 0])
Z3 = Y3 * np.tan(angle)