Регрессия гребня с помощью `glmnet` дает другие коэффициенты, чем те, которые я вычисляю по" определению учебника "

Question

Я бегу Ридж регрессии с использованием glmnetR пакет. Я заметил, что коэффициенты, которые я получаю из glmnet::glmnet Функции отличаются от тех, которые я получаю, вычисляя коэффициенты по определению (с использованием одного и того же значения лямбды). Может кто-нибудь объяснить мне, почему?

Данные (оба: ответ Y и дизайн матрицы X) масштабируются.

library(MASS)
library(glmnet)

# Data dimensions
p.tmp <- 100
n.tmp <- 100

# Data objects
set.seed(1)
X <- scale(mvrnorm(n.tmp, mu = rep(0, p.tmp), Sigma = diag(p.tmp)))
beta <- rep(0, p.tmp)
beta[sample(1:p.tmp, 10, replace = FALSE)] <- 10
Y.true <- X %*% beta
Y <- scale(Y.true + matrix(rnorm(n.tmp))) # Y.true + Gaussian noise

# Run glmnet 
ridge.fit.cv <- cv.glmnet(X, Y, alpha = 0)
ridge.fit.lambda <- ridge.fit.cv$lambda.1se

# Extract coefficient values for lambda.1se (without intercept)
ridge.coef <- (coef(ridge.fit.cv, s = ridge.fit.lambda))[2:(p.tmp+1)]

# Get coefficients "by definition"
ridge.coef.DEF <- solve(t(X) %*% X + ridge.fit.lambda * diag(p.tmp)) %*% t(X) %*% Y

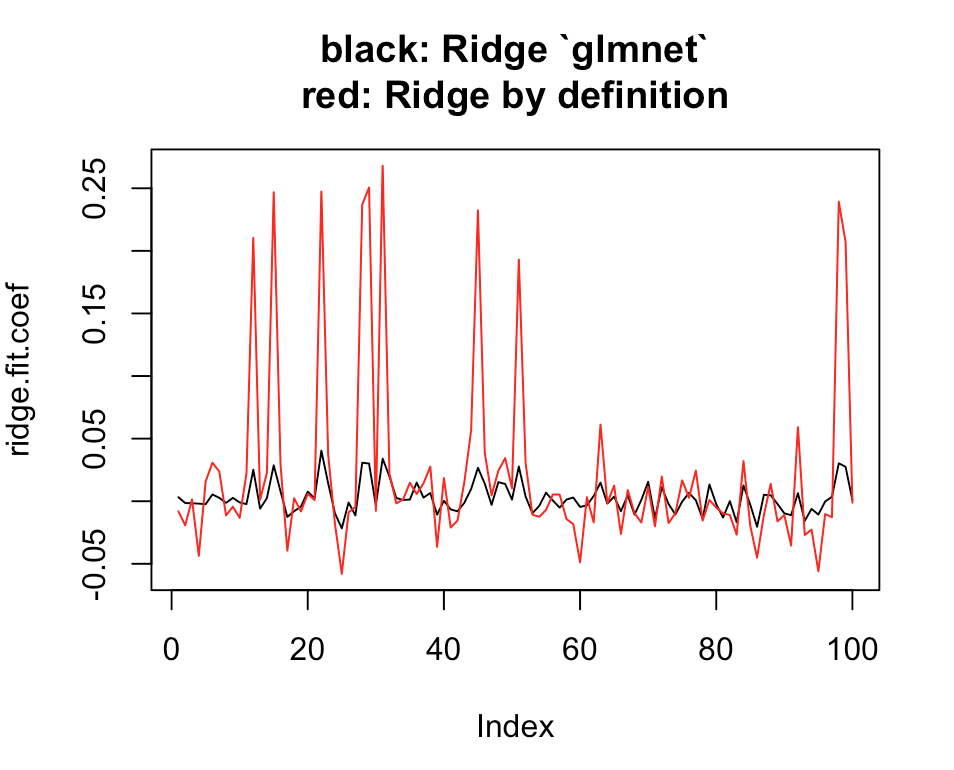
# Plot estimates
plot(ridge.coef, type = "l", ylim = range(c(ridge.coef, ridge.coef.DEF)),
     main = "black: Ridge `glmnet`\nred: Ridge by definition")
lines(ridge.coef.DEF, col = "red")

Answer 1

Если вы читаете ?glmnet, вы увидите, что штрафная целевая функция гауссовского ответа:

1/2 * RSS / nobs + lambda * penalty

В случае штрафа 1/2 * ||beta_j||_2^2 используется, у нас есть

1/2 * RSS / nobs + 1/2 * lambda * ||beta_j||_2^2

который пропорционален

RSS + lambda * nobs * ||beta_j||_2^2

Это отличается от того, что мы обычно видим в учебнике относительно регрессии гребня:

RSS + lambda * ||beta_j||_2^2

Формула, которую вы пишете:

##solve(t(X) %*% X + ridge.fit.lambda * diag(p.tmp)) %*% t(X) %*% Y
drop(solve(crossprod(X) + diag(ridge.fit.lambda, p.tmp), crossprod(X, Y)))

для результата учебника; за glmnet мы должны ожидать:

##solve(t(X) %*% X + n.tmp * ridge.fit.lambda * diag(p.tmp)) %*% t(X) %*% Y
drop(solve(crossprod(X) + diag(n.tmp * ridge.fit.lambda, p.tmp), crossprod(X, Y)))

Так, в учебнике используются штрафные наименьшие квадраты, но glmnet использует штрафованную среднеквадратичную ошибку.

Обратите внимание, что я не использовал ваш оригинальный код с t(), "%*%" а также solve(A) %*% b; с помощью crossprod а также solve(A, b) более эффективно! См. Раздел " Последующие действия " в конце.

---

Теперь давайте сделаем новое сравнение:

library(MASS)
library(glmnet)

# Data dimensions
p.tmp <- 100
n.tmp <- 100

# Data objects
set.seed(1)
X <- scale(mvrnorm(n.tmp, mu = rep(0, p.tmp), Sigma = diag(p.tmp)))
beta <- rep(0, p.tmp)
beta[sample(1:p.tmp, 10, replace = FALSE)] <- 10
Y.true <- X %*% beta
Y <- scale(Y.true + matrix(rnorm(n.tmp)))

# Run glmnet 
ridge.fit.cv <- cv.glmnet(X, Y, alpha = 0, intercept = FALSE)
ridge.fit.lambda <- ridge.fit.cv$lambda.1se

# Extract coefficient values for lambda.1se (without intercept)
ridge.coef <- (coef(ridge.fit.cv, s = ridge.fit.lambda))[-1]

# Get coefficients "by definition"
ridge.coef.DEF <- drop(solve(crossprod(X) + diag(n.tmp * ridge.fit.lambda, p.tmp), crossprod(X, Y)))

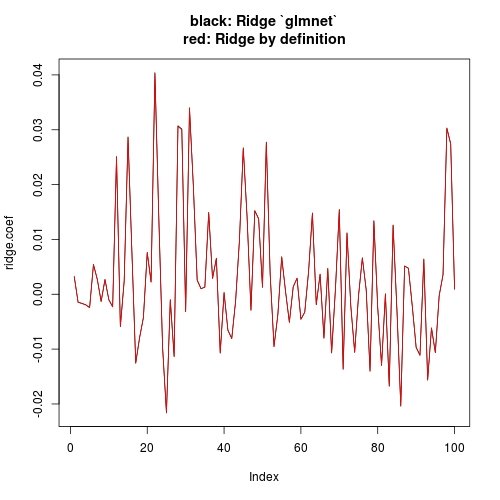
# Plot estimates
plot(ridge.coef, type = "l", ylim = range(c(ridge.coef, ridge.coef.DEF)),
     main = "black: Ridge `glmnet`\nred: Ridge by definition")
lines(ridge.coef.DEF, col = "red")

Обратите внимание, что я установил intercept = FALSE когда я звоню cv.glmnet (или же glmnet). Это имеет более концептуальное значение, чем то, что будет влиять на практике. Концептуально, наши вычисления в учебнике не имеют перехвата, поэтому мы хотим отбросить перехват при использовании glmnet, Но практически, так как ваш X а также Y стандартизированы, теоретическая оценка пересечения равна 0. Даже с intercepte = TRUE (glment по умолчанию), вы можете проверить, что оценка перехвата ~e-17 (численно 0), следовательно, оценка других коэффициентов не сильно пострадала. Другой ответ просто показывает это.

---

Следовать за

Что касается использования crossprod а также solve(A, b) - интересно! У вас случайно есть какое-либо упоминание о сравнении симуляции для этого?

t(X) %*% Y сначала возьму транспонировать X1 <- t(X) тогда делай X1 %*% Y, в то время как crossprod(X, Y) не будет делать транспонирование. "%*%" это обертка для DGEMM на случай op(A) = A, op(B) = B, в то время как crossprod это обертка для op(A) = A', op(B) = B, так же tcrossprod за op(A) = A, op(B) = B',

Основное использование crossprod(X) для t(X) %*% X; аналогично tcrossprod(X) за X %*% t(X), в таком случае DSYRK вместо DGEMM называется. Вы можете прочитать первый раздел " Почему встроенная функция lm так медленно работает в R"? для разума и ориентира.

Знать, что если X не квадратная матрица, crossprod(X) а также tcrossprod(X) не одинаково быстры, так как в них задействовано различное количество операций с плавающей запятой, для чего вы можете прочитать дополнительное замечание о любой более быстрой функции R, чем "tcrossprod", для симметричного умножения с плотной матрицей?

относительно solvel(A, b) а также solve(A) %*% b Пожалуйста, прочитайте первый раздел Как эффективно вычислить diag (X%% solve (A) %% t (X)) без обратной матрицы?

Answer 2

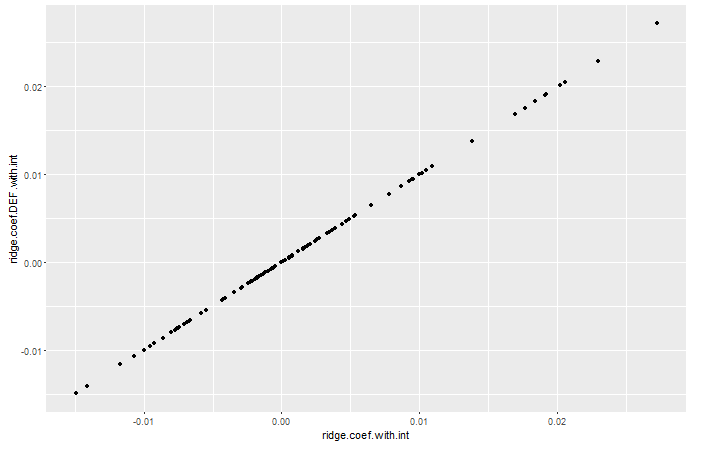
Добавляя к интересному сообщению Чжэюаня, мы провели еще несколько экспериментов, чтобы увидеть, что мы можем получить те же результаты с перехватом, как показано ниже:

# ridge with intercept glmnet
ridge.fit.cv.int <- cv.glmnet(X, Y, alpha = 0, intercept = TRUE, family="gaussian")
ridge.fit.lambda.int <- ridge.fit.cv.int$lambda.1se
ridge.coef.with.int <- as.vector(as.matrix(coef(ridge.fit.cv.int, s = ridge.fit.lambda.int)))

# ridge with intercept definition, use the same lambda obtained with cv from glmnet
X.with.int <- cbind(1, X)
ridge.coef.DEF.with.int <- drop(solve(crossprod(X.with.int) + ridge.fit.lambda.int * diag(n.tmp, p.tmp+1), crossprod(X.with.int, Y)))

ggplot() + geom_point(aes(ridge.coef.with.int, ridge.coef.DEF.with.int))

# comupte residuals
RSS.fit.cv.int <- sum((Y.true - predict(ridge.fit.cv.int, newx=X))^2) # predict adds inter
RSS.DEF.int <- sum((Y.true - X.with.int %*% ridge.coef.DEF.with.int)^2)

RSS.fit.cv.int
[1] 110059.9
RSS.DEF.int
[1] 110063.4