Точка за пределами области, которая ближе всего к точке внутри?
У меня есть программа, в которой сущность движется в двухмерном пространстве. Чтобы перейти на один шаг, сущность выбирает свою следующую точку, а затем устанавливает ее в качестве своей текущей точки.
Однако иногда следующая точка сущности заключается в Area (java.awt.geom.Area), что запрещено ("запретная зона" на самом деле является скоростным препятствием).
Как организация может выбрать точку за пределами Area что ближе всего к предпочтительной точке организации?
Area состоит из разных форм (иногда фигуры не соприкасаются).
Мой первоначальный план состоял в том, чтобы просто нарисовать линию до предпочтительной точки. Везде, где линия пересекла Area Во-первых, это будет следующий лучший момент. Тем не менее, найти пересечение между линией и Area оказывается довольно сложным.
РЕДАКТИРОВАТЬ: Это не обязательно найти ближайший пункт. Это будет просто найти точку шкафа на той же траектории. Я ищу ближайшую возможную точку.
возможно Area не лучший класс для использования. Все, что мне нужно, это то, что может добавить несколько фигур, даже если фигуры не соприкасаются.
4 ответа
Я решил проблему:
Сначала найдите все отрезки, которые ограничивают Area, Я написал код, чтобы сделать это на другой ответ.
Затем нужно просто выполнить итерацию по каждому сегменту линии и записать точку на сегменте, ближайшую к желаемой точке объекта. Сохраните их в структуре данных по вашему выбору (например, ArrayList).
См.: Наименьшее расстояние между точкой и отрезком
Наконец, определите, какая из точек ближе всего к желаемой точке. Вуаля!
Вот демонстрация:
import java.awt.Color;
import java.awt.Dimension;
import java.awt.Graphics;
import java.awt.Graphics2D;
import java.awt.geom.Area;
import java.awt.geom.Ellipse2D;
import java.awt.geom.Line2D;
import java.awt.geom.Path2D;
import java.awt.geom.PathIterator;
import java.awt.geom.Point2D;
import java.util.ArrayList;
import java.util.Random;
import javax.swing.JFrame;
public class AreaTest extends JFrame{
private static final long serialVersionUID = -2221432546854106311L;
Area area = new Area();
ArrayList<Line2D.Double> areaSegments = new ArrayList<Line2D.Double>();
Point2D.Double insidePoint = new Point2D.Double(225, 225);
Point2D.Double closestPoint = new Point2D.Double(-1, -1);
Point2D.Double bestPoint = new Point2D.Double(-1, -1);
ArrayList<Point2D.Double> closestPointList = new ArrayList<Point2D.Double>();
AreaTest() {
Path2D.Double triangle = new Path2D.Double();
Random random = new Random();
// Draw three random triangles
for (int i = 0; i < 3; i++) {
triangle.moveTo(random.nextInt(400) + 50, random.nextInt(400) + 50);
triangle.lineTo(random.nextInt(400) + 50, random.nextInt(400) + 50);
triangle.lineTo(random.nextInt(400) + 50, random.nextInt(400) + 50);
triangle.closePath();
area.add(new Area(triangle));
triangle.reset();
}
// Place a point inside the area
if (!area.contains(insidePoint)); {
while (!area.contains(insidePoint)) {
insidePoint.setLocation(random.nextInt(400) + 50, random.nextInt(400) + 50);
}
}
// Note: we're storing double[] and not Point2D.Double
ArrayList<double[]> areaPoints = new ArrayList<double[]>();
double[] coords = new double[6];
for (PathIterator pi = area.getPathIterator(null); !pi.isDone(); pi.next()) {
// Because the Area is composed of straight lines
int type = pi.currentSegment(coords);
// We record a double array of {segment type, x coord, y coord}
double[] pathIteratorCoords = {type, coords[0], coords[1]};
areaPoints.add(pathIteratorCoords);
}
double[] start = new double[3]; // To record where each polygon starts
for (int i = 0; i < areaPoints.size(); i++) {
// If we're not on the last point, return a line from this point to the next
double[] currentElement = areaPoints.get(i);
// We need a default value in case we've reached the end of the ArrayList
double[] nextElement = {-1, -1, -1};
if (i < areaPoints.size() - 1) {
nextElement = areaPoints.get(i + 1);
}
// Make the lines
if (currentElement[0] == PathIterator.SEG_MOVETO) {
start = currentElement; // Record where the polygon started to close it later
}
if (nextElement[0] == PathIterator.SEG_LINETO) {
areaSegments.add(
new Line2D.Double(
currentElement[1], currentElement[2],
nextElement[1], nextElement[2]
)
);
} else if (nextElement[0] == PathIterator.SEG_CLOSE) {
areaSegments.add(
new Line2D.Double(
currentElement[1], currentElement[2],
start[1], start[2]
)
);
}
}
// Calculate the nearest point on the edge
for (Line2D.Double line : areaSegments) {
// From: https://stackru.com/questions/6176227
double u =
((insidePoint.getX() - line.x1) * (line.x2 - line.x1) + (insidePoint.getY() - line.y1) * (line.y2 - line.y1))
/ ((line.x2 - line.x1) * (line.x2 - line.x1) + (line.y2 - line.y1) * (line.y2 - line.y1));
double xu = line.x1 + u * (line.x2 - line.x1);
double yu = line.y1 + u * (line.y2 - line.y1);
if (u < 0) {
closestPoint.setLocation(line.getP1());
} else if (u > 1) {
closestPoint.setLocation(line.getP2());
} else {
closestPoint.setLocation(xu, yu);
}
closestPointList.add((Point2D.Double) closestPoint.clone());
if (closestPoint.distance(insidePoint) < bestPoint.distance(insidePoint)) {
bestPoint.setLocation(closestPoint);
}
}
setSize(new Dimension(500, 500));
setLocationRelativeTo(null); // To center the JFrame on screen
setDefaultCloseOperation(EXIT_ON_CLOSE);
setResizable(false);
setVisible(true);
}
public void paint(Graphics g) {
// Fill the area
Graphics2D g2d = (Graphics2D) g;
g.setColor(Color.lightGray);
g2d.fill(area);
// Draw the border line by line
g.setColor(Color.black);
for (Line2D.Double line : areaSegments) {
g2d.draw(line);
}
// Draw the inside point
g.setColor(Color.red);
g2d.fill(
new Ellipse2D.Double(
insidePoint.getX() - 3,
insidePoint.getY() - 3,
6,
6
)
);
// Draw the other close points
for (Point2D.Double point : closestPointList) {
g.setColor(Color.black);
g2d.fill(
new Ellipse2D.Double(
point.getX() - 3,
point.getY() - 3,
6,
6
)
);
}
// Draw the outside point
g.setColor(Color.green);
g2d.fill(
new Ellipse2D.Double(
bestPoint.getX() - 3,
bestPoint.getY() - 3,
6,
6
)
);
}
public static void main(String[] args) {
new AreaTest();
}
}
Вот результат:
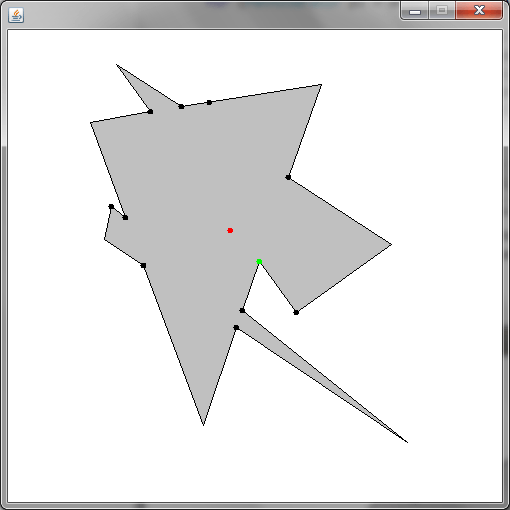
И опять:

Посмотреть мой ответ на этот пост
Вы можете получить ближайшую точку за пределами многоугольника с помощью простого и легкого подхода:
Просто найдите ближайший линейный сегмент и найдите перпендикулярный угол к тому сегменту, который пересекает точку ввода.
Пример кода:
Vector2 - 2 двойных, x и y (как в Unity)
public class PolyCollisions {
// Call this function...
public static Vector2 doCollisions (Vector2[] polygon, Vector2 point) {
if(!pointIsInPoly(polygon, point)) {
// The point is not colliding with the polygon, so it does not need to change location
return point;
}
// Get the closest point off the polygon
return closestPointOutsidePolygon(polygon, point);
}
// Check if the given point is within the given polygon (Vertexes)
//
// If so, call on collision if required, and move the point to the
// closest point outside of the polygon
public static boolean pointIsInPoly(Vector2[] verts, Vector2 p) {
int nvert = verts.length;
double[] vertx = new double[nvert];
double[] verty = new double[nvert];
for(int i = 0; i < nvert; i++) {
Vector2 vert = verts[i];
vertx[i] = vert.x;
verty[i] = vert.y;
}
double testx = p.x;
double testy = p.y;
int i, j;
boolean c = false;
for (i = 0, j = nvert-1; i < nvert; j = i++) {
if ( ((verty[i]>testy) != (verty[j]>testy)) &&
(testx < (vertx[j]-vertx[i]) * (testy-verty[i]) / (verty[j]-verty[i]) + vertx[i]) )
c = !c;
}
return c;
}
// Gets the closed point that isn't inside the polygon...
public static Vector2 closestPointOutsidePolygon (Vector2[] poly, Vector2 point) {
return getClosestPointInSegment(closestSegment(poly, point), point);
}
public static Vector2 getClosestPointInSegment (Vector2[] segment, Vector2 point) {
return newPointFromCollision(segment[0], segment[1], point);
}
public static Vector2 newPointFromCollision (Vector2 aLine, Vector2 bLine, Vector2 p) {
return nearestPointOnLine(aLine.x, aLine.y, bLine.x, bLine.y, p.x, p.y);
}
public static Vector2 nearestPointOnLine(double ax, double ay, double bx, double by, double px, double py) {
// https://stackru.com/questions/1459368/snap-point-to-a-line-java
double apx = px - ax;
double apy = py - ay;
double abx = bx - ax;
double aby = by - ay;
double ab2 = abx * abx + aby * aby;
double ap_ab = apx * abx + apy * aby;
double t = ap_ab / ab2;
if (t < 0) {
t = 0;
} else if (t > 1) {
t = 1;
}
return new Vector2(ax + abx * t, ay + aby * t);
}
public static Vector2[] closestSegment (Vector2[] points, Vector2 point) {
Vector2[] returns = new Vector2[2];
int index = closestPointIndex(points, point);
returns[0] = points[index];
Vector2[] neighbors = new Vector2[] {
points[(index+1+points.length)%points.length],
points[(index-1+points.length)%points.length]
};
double[] neighborAngles = new double[] {
getAngle(new Vector2[] {point, returns[0], neighbors[0]}),
getAngle(new Vector2[] {point, returns[0], neighbors[1]})
};
if(neighborAngles[0] < neighborAngles[1]) {
returns[1] = neighbors[0];
} else {
returns[1] = neighbors[0];
}
return returns;
}
public static double getAngle (Vector2[] abc) {
// https://stackru.com/questions/1211212/how-to-calculate-an-angle-from-three-points
// atan2(P2.y - P1.y, P2.x - P1.x) - atan2(P3.y - P1.y, P3.x - P1.x)
return Math.atan2(abc[2].y - abc[0].y, abc[2].x - abc[0].x) - Math.atan2(abc[1].y - abc[0].y, abc[1].x - abc[0].x);
}
//public static Vector2 lerp (Vector2 a, Vector2 b, double c) {
//
// return new Vector2(c*(a.x-b.x)+b.x, c*(a.y-b.y)+b.y);
//
//}
/*public static Vector2 closestPoint (Vector2[] points, Vector2 point) {
int leastDistanceIndex = 0;
double leastDistance = Double.MAX_VALUE;
for(int i = 0; i < points.length; i++) {
double dist = distance(points[i], point);
if(dist < leastDistance) {
leastDistanceIndex = i;
leastDistance = dist;
}
}
return points[leastDistanceIndex];
}*/
public static int closestPointIndex (Vector2[] points, Vector2 point) {
int leastDistanceIndex = 0;
double leastDistance = Double.MAX_VALUE;
for(int i = 0; i < points.length; i++) {
double dist = distance(points[i], point);
if(dist < leastDistance) {
leastDistanceIndex = i;
leastDistance = dist;
}
}
return leastDistanceIndex;
}
public static double distance (Vector2 a, Vector2 b) {
return Math.sqrt(Math.pow(Math.abs(a.x-b.x), 2)+Math.pow(Math.abs(a.y-b.y), 2));
}
}
Полезные ссылки / ответы
Формула для расстояния между двумя точками (javascript):
var xDiff = ( point1x - point2x ),
yDiff = ( point1y - point2y ),
distance = Math.sqrt( ( xDiff * xDiff ) + ( yDiff * yDiff ) );
Обведите "предложенную новую точку", начиная с одного x-1, y-1 to x+1, y+1, В каждой точке проверяйте, чтобы убедиться, что это не запрещенная точка, не точка, из которой вы только что пришли, и не за пределами карты. Если он соответствует всем этим критериям, используйте приведенную выше формулу для измерения расстояния и добавьте его в массив. В конце цикла "1-point out" проверьте, есть ли какие-либо расстояния в этом массиве. Если так, возьмите самый маленький и все готово. Если их нет, переходите на x-2, y-2 to x+2, y+2 (2 балла).
Это будет очень быстро для небольшой области, на которую вы ссылаетесь.
Демо: http://jsfiddle.net/ThinkingStiff/V7Bqm/
var X = 0,
Y = 1,
currentPoint = [5,5],
proposedPoint = [5,6],
forbiddenPoints = [[5,6],[6,6],[4,7],[5,7],[6,7],[4,8],[5,8]],
map = { left:1, top:1, right:10, bottom:10 };
function closestSafePoint( point ) {
var x = point[X], y = point[Y], safePoints = [];
for( var left = x - 1, top = y - 1, right = x + 1, bottom = y + 1;
left <= map.left || top <= map.top || right <= map.right || bottom <= map.bottom;
left--, top--, right++, bottom++) {
checkHorizontalPoints( safePoints, point, left, right, top );
checkHorizontalPoints( safePoints, point, left, right, bottom );
checkVerticalPoints( safePoints, point, top + 1, bottom - 1, left );
checkVerticalPoints( safePoints, point, top + 1, bottom - 1, right );
safePoints.sort( function( a, b ){ return a[1] - b[1] } );
return safePoints.length ? safePoints[0] : point;
};
};
function checkHorizontalPoints( points, fromPoint, startX, endX, y ) {
for( var x = startX; x <= endX ; x++ ) {
var toPoint = [x, y];
if( !isForbidden( toPoint ) && !isCurrent( toPoint) && onMap( toPoint ) ) {
points.push( [toPoint, distance( fromPoint, toPoint )] );
};
};
};
function checkVerticalPoints( points, fromPoint, startY, endY, x ) {
for( var y = startY; y <= endY ; y++ ) {
var toPoint = [x, y];
if( !isForbidden( toPoint ) && !isCurrent( toPoint) && onMap( toPoint ) ) {
points.push( [toPoint, distance( fromPoint, toPoint )] );
};
};
};
function isForbidden( point ) {
for( var index = 0; index < forbiddenPoints.length; index++ ) {
if( forbiddenPoints[index].toString() == point.toString() ) return true;
};
};
function isCurrent( point ) {
return currentPoint.toString() == point.toString() ? true : false;
};
function onMap( point ) {
var x = point[X], y = point[Y];
return x >= map.left && y >= map.top && x <= map.right && y <= map.bottom;
};
function distance( pointA, pointB ) {
var xDiff = ( pointA[X] - pointB[X] ),
yDiff = ( pointA[Y] - pointB[Y] );
return Math.sqrt( ( xDiff * xDiff ) + ( yDiff * yDiff ) );
};
console.log(
'current: ' + currentPoint + ', '
+ 'proposed: ' + proposedPoint + ', '
+ 'closest: ' + closestSafePoint( proposedPoint )[0]
);
Одна из оптимизаций, которую вы могли бы сделать для этого, если вы уверены, что большинство ваших безопасных точек будут на расстоянии одного или двух пунктов, - это пробиться, как только вы достигнете точки, расстояние которой будет таким же, как и на уровне, на котором вы находитесь., Так что, если вы находитесь на первом цикле, и вы получите точку, которая является расстоянием = 1, остановитесь, так как вы никогда не станете ближе, чем это.
ОБНОВЛЕНИЕ: я заметил, что вы добавили "ту же траекторию" к вашему вопросу. Но в одном из комментариев вы также говорите, что он не может перепрыгнуть через запрещенную область. Эти заявления, кажется, противоречат друг другу.
Та же траектория немного сложнее и требует некоторого триггера. Проверьте мою демонстрацию круговых divs на http://jsfiddle.net/ThinkingStiff/uLu7v/. На полпути вниз есть функция "точка на луче":
$this.siblings( ".circle" ).each( function()
Это вычисляет расстояние, чтобы переместить окружающие круги на луче от выбранного круга. Это может быть использовано для расчета точки на вашей траектории. Но я думаю, что моя первоначальная функция - это то, что вы ищете, и вы не имели в виду ту же траекторию.
Самый легкий (и самый неэффективный) подход - грубая сила. У вас есть предпочтительная точка внутри области. чтобы найти ближайшую к нему точку: удерживайте две переменные, одну для минимального расстояния и одну для текущей ближайшей точки. Теперь просто перешагните через любую другую точку в вашем двухмерном пространстве: если эта точка не находится внутри запрещенной области (или любой запрещенной области, если их много), то вычислите расстояние между ней и предпочтительной точкой. Если это расстояние меньше текущего минимального расстояния, сделайте так, чтобы оно стало текущим минимальным расстоянием, и сделайте точку текущей текущей ближайшей точкой. когда вы закончите, у вас будет ближайшая точка за пределами области, и если ничего не было найдено, вы останетесь на своей исходной точке.
Я не специалист по геометрическим алгоритмам, но если двумерное пространство очень велико и вычисления не завершаются достаточно быстро, возможно, вы можете попытаться улучшить его следующим образом: в классе Area есть метод contains, который "проверяет, является ли внутреннее пространство формы полностью содержит указанную прямоугольную область ". поэтому начните создавать прямоугольники (или квадраты) вокруг предпочтительной точки. вы начинаете с минимального прямоугольника, окружающего точку, и в каждом цикле вы увеличиваете его на одну точку в каждом направлении. для каждого прямоугольника, который вы создаете, проверьте, содержится ли он в области. Вы останавливаете вычисление прямоугольников, когда вы нажимаете на первый прямоугольник, который не полностью содержится в области. затем вы используете вышеупомянутый алгоритм (грубая сила), но только для точек, содержащихся в этом прямоугольнике и не находящихся внутри области.
