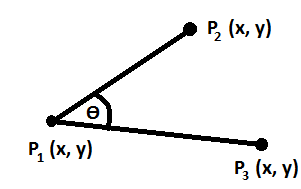Как рассчитать угол из трех точек?
Допустим, у вас есть это:
P1 = (x=2, y=50)
P2 = (x=9, y=40)
P3 = (x=5, y=20)
Предположим, что P1 является центральной точкой круга. Это всегда то же самое. Я хочу угол, который состоит из P2 а также P3или, другими словами, угол, который находится рядом с P1, Внутренний угол, чтобы быть точным. Это всегда будет острый угол, поэтому менее -90 градусов.
Я подумал: чувак, это простая геометрия математики. Но я искал формулу около 6 часов и обнаружил, что люди говорят только о сложных вещах НАСА, таких как arccos и векторные скалярные продукты. Моя голова чувствует себя как в холодильнике.
Некоторые математические гуру, которые думают, что это простая проблема? Я не думаю, что язык программирования здесь имеет значение, но для тех, кто думает, что это имеет значение: Java и Objective-C. Мне нужно это для обоих, но я не пометил это для них.
16 ответов
Если вы имеете в виду угол, который является вершиной P1, то использование закона косинуса должно работать:
агссоз((P122 + P132 - P232) / (2 * P12 * P13))
где P12 - длина сегмента от P1 до P2, рассчитанная по
sqrt ((P1x - P2x)2 + (P1y - P2y)2)
Это становится очень просто, если вы думаете, что это два вектора, один из точки P1 в P2 и один из P1 в P3
так:
a = (p1.x - p2.x, p1.y - p2.y)
b = (p1.x - p3.x, p1.y - p3.y)
Затем вы можете инвертировать формулу точечного произведения: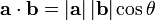
чтобы получить угол: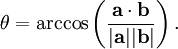
Помни что 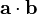 просто означает:
a1*b1 + a2*b2 (только 2 измерения здесь...)
просто означает:
a1*b1 + a2*b2 (только 2 измерения здесь...)
Лучший способ справиться с вычислением углов - это использовать atan2(y, x) это дало точку x, y возвращает угол от этой точки и X+ ось относительно происхождения.
Учитывая, что вычисление
double result = atan2(P3.y - P1.y, P3.x - P1.x) -
atan2(P2.y - P1.y, P2.x - P1.x);
т.е. вы в основном переводите две точки -P1 (другими словами, вы переводите все так, чтобы P1 заканчивается в начале координат), а затем вы учитываете разницу абсолютных углов P3 и из P2,
Преимущества atan2 является то, что представлен полный круг (вы можете получить любое число между -π и π), где вместо acos вам нужно обработать несколько случаев в зависимости от признаков, чтобы вычислить правильный результат.
Единственная особая точка для atan2 является (0, 0)... это означает, что оба P2 а также P3 должен отличаться от P1 как в этом случае не имеет смысла говорить о ракурсе.
Позвольте мне привести пример на JavaScript, я много с этим боролся:
/**
* Calculates the angle (in radians) between two vectors pointing outward from one center
*
* @param p0 first point
* @param p1 second point
* @param c center point
*/
function find_angle(p0,p1,c) {
var p0c = Math.sqrt(Math.pow(c.x-p0.x,2)+
Math.pow(c.y-p0.y,2)); // p0->c (b)
var p1c = Math.sqrt(Math.pow(c.x-p1.x,2)+
Math.pow(c.y-p1.y,2)); // p1->c (a)
var p0p1 = Math.sqrt(Math.pow(p1.x-p0.x,2)+
Math.pow(p1.y-p0.y,2)); // p0->p1 (c)
return Math.acos((p1c*p1c+p0c*p0c-p0p1*p0p1)/(2*p1c*p0c));
}
Бонус: пример с HTML5-canvas
В основном, у вас есть два вектора, один вектор из P1 в P2 и другой из P1 в P3. Так что все, что вам нужно, это формула для расчета угла между двумя векторами.
Посмотрите здесь для хорошего объяснения и формулы.
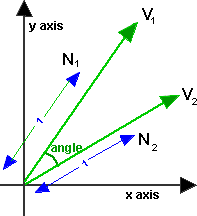
Если вы думаете о P1 как о центре круга, вы думаете, что это слишком сложно. У вас есть простой треугольник, поэтому ваша проблема разрешима с помощью закона косинусов. Нет необходимости в какой-либо трансформации полярной координаты или что-то в этом роде. Скажем, расстояния P1-P2 = A, P2-P3 = B и P3-P1 = C:
Угол = Арккос ( (B^2-A^2-C^2) / 2AC)
Все, что вам нужно сделать, это рассчитать длину расстояний A, B и C. Они легко доступны из x- и y-координат ваших точек и теоремы Пифагора.
Длина = sqrt( (X2-X1)^2 + (Y2-Y1)^2)
Недавно я столкнулся с подобной проблемой, только мне нужно было различать положительный и отрицательный углы. В случае, если это кому-нибудь пригодится, я рекомендую фрагмент кода, который я взял из этого списка рассылки, об обнаружении поворота поверх события касания для Android:
@Override
public boolean onTouchEvent(MotionEvent e) {
float x = e.getX();
float y = e.getY();
switch (e.getAction()) {
case MotionEvent.ACTION_MOVE:
//find an approximate angle between them.
float dx = x-cx;
float dy = y-cy;
double a=Math.atan2(dy,dx);
float dpx= mPreviousX-cx;
float dpy= mPreviousY-cy;
double b=Math.atan2(dpy, dpx);
double diff = a-b;
this.bearing -= Math.toDegrees(diff);
this.invalidate();
}
mPreviousX = x;
mPreviousY = y;
return true;
}
Очень простое геометрическое решение с объяснением
Несколько дней назад тот же самый человек попал в ту же задачу и должен был сидеть с книгой по математике. Я решил проблему путем объединения и упрощения некоторых основных формул.
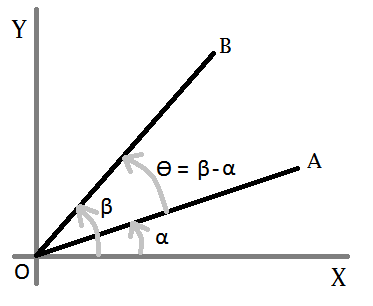
Давайте рассмотрим эту цифру
Мы хотим знать ϴ, поэтому нам нужно сначала выяснить α и β. Теперь для любой прямой
y = m * x + c
Пусть -A = (ax, ay), B = (bx, by) и O = (ox, oy). Так что для линии ОА -
oy = m1 * ox + c ⇒ c = oy - m1 * ox ...(eqn-1)
ay = m1 * ax + c ⇒ ay = m1 * ax + oy - m1 * ox [from eqn-1]
⇒ ay = m1 * ax + oy - m1 * ox
⇒ m1 = (ay - oy) / (ax - ox)
⇒ tan α = (ay - oy) / (ax - ox) [m = slope = tan ϴ] ...(eqn-2)
Точно так же для линии OB -
tan β = (by - oy) / (bx - ox) ...(eqn-3)
Теперь нам нужно ϴ = β - α, В тригонометрии мы имеем формулу
tan (β-α) = (tan β + tan α) / (1 - tan β * tan α) ...(eqn-4)
После замены значения tan α (из уравнения-2) и tan b (из уравнения-3) в уравнении-4, и, применяя упрощение, получаем
tan (β-α) = ( (ax-ox)*(by-oy)+(ay-oy)*(bx-ox) ) / ( (ax-ox)*(bx-ox)-(ay-oy)*(by-oy) )
Так,
ϴ = β-α = tan^(-1) ( ((ax-ox)*(by-oy)+(ay-oy)*(bx-ox)) / ((ax-ox)*(bx-ox)-(ay-oy)*(by-oy)) )
Вот и все!
Теперь возьмите следующую цифру
Этот C# или Java-метод вычисляет угол (ϴ) -
private double calculateAngle(double P1X, double P1Y, double P2X, double P2Y,
double P3X, double P3Y){
double numerator = P2Y*(P1X-P3X) + P1Y*(P3X-P2X) + P3Y*(P2X-P1X);
double denominator = (P2X-P1X)*(P1X-P3X) + (P2Y-P1Y)*(P1Y-P3Y);
double ratio = numerator/denominator;
double angleRad = Math.Atan(ratio);
double angleDeg = (angleRad*180)/Math.PI;
if(angleDeg<0){
angleDeg = 180+angleDeg;
}
return angleDeg;
}
В Objective-C вы можете сделать это
float xpoint = (((atan2((newPoint.x - oldPoint.x) , (newPoint.y - oldPoint.y)))*180)/M_PI);
Или читайте больше здесь
Вы упомянули угол со знаком (-90). Во многих приложениях углы могут иметь знаки (положительные и отрицательные, см. http://en.wikipedia.org/wiki/Angle). Если точки (скажем) P2(1,0), P1(0,0), P3(0,1), то угол P3-P1-P2 условно положителен (PI/2), тогда как угол P2-P1- Р3 отрицательный. Использование длин сторон не будет различать + и -, поэтому, если это имеет значение, вам нужно будет использовать векторы или такие функции, как Math.atan2(a, b).
Углы также могут выходить за пределы 2*PI, и хотя это не относится к текущему вопросу, было достаточно важно, чтобы я написал свой собственный класс Angle (также чтобы убедиться, что градусы и радианы не перепутаны). Вопросы относительно того, будет ли угол1 меньше, чем угол2, критически зависят от того, как определяются углы. Также может быть важно решить, будет ли строка (-1,0)(0,0)(1,0) представлена как Math.PI или -Math.PI
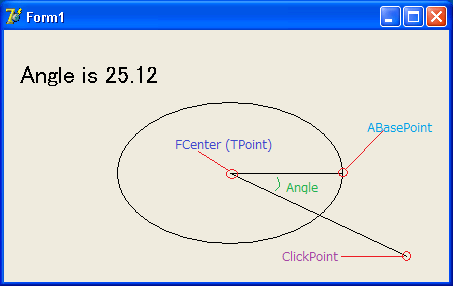
В последнее время у меня тоже такая же проблема... В Delphi она очень похожа на Objective-C.
procedure TForm1.FormPaint(Sender: TObject);
var ARect: TRect;
AWidth, AHeight: Integer;
ABasePoint: TPoint;
AAngle: Extended;
begin
FCenter := Point(Width div 2, Height div 2);
AWidth := Width div 4;
AHeight := Height div 4;
ABasePoint := Point(FCenter.X+AWidth, FCenter.Y);
ARect := Rect(Point(FCenter.X - AWidth, FCenter.Y - AHeight),
Point(FCenter.X + AWidth, FCenter.Y + AHeight));
AAngle := ArcTan2(ClickPoint.Y-Center.Y, ClickPoint.X-Center.X) * 180 / pi;
AngleLabel.Caption := Format('Angle is %5.2f', [AAngle]);
Canvas.Ellipse(ARect);
Canvas.MoveTo(FCenter.X, FCenter.Y);
Canvas.LineTo(FClickPoint.X, FClickPoint.Y);
Canvas.MoveTo(FCenter.X, FCenter.Y);
Canvas.LineTo(ABasePoint.X, ABasePoint.Y);
end;
function p(x, y) {return {x,y}}
function normaliseToInteriorAngle(angle) {
if (angle < 0) {
angle += (2*Math.PI)
}
if (angle > Math.PI) {
angle = 2*Math.PI - angle
}
return angle
}
function angle(p1, center, p2) {
const transformedP1 = p(p1.x - center.x, p1.y - center.y)
const transformedP2 = p(p2.x - center.x, p2.y - center.y)
const angleToP1 = Math.atan2(transformedP1.y, transformedP1.x)
const angleToP2 = Math.atan2(transformedP2.y, transformedP2.x)
return normaliseToInteriorAngle(angleToP2 - angleToP1)
}
function toDegrees(radians) {
return 360 * radians / (2 * Math.PI)
}
console.log(toDegrees(angle(p(-10, 0), p(0, 0), p(0, -10))))Вот метод C# для возврата угла (0-360) против часовой стрелки от горизонтали для точки на окружности.
public static double GetAngle(Point centre, Point point1)
{
// Thanks to Dave Hill
// Turn into a vector (from the origin)
double x = point1.X - centre.X;
double y = point1.Y - centre.Y;
// Dot product u dot v = mag u * mag v * cos theta
// Therefore theta = cos -1 ((u dot v) / (mag u * mag v))
// Horizontal v = (1, 0)
// therefore theta = cos -1 (u.x / mag u)
// nb, there are 2 possible angles and if u.y is positive then angle is in first quadrant, negative then second quadrant
double magnitude = Math.Sqrt(x * x + y * y);
double angle = 0;
if(magnitude > 0)
angle = Math.Acos(x / magnitude);
angle = angle * 180 / Math.PI;
if (y < 0)
angle = 360 - angle;
return angle;
}
Ура, Пол
Есть простой ответ на это с использованием математики средней школы..
Допустим, у вас есть 3 балла
Чтобы получить угол от точки А до Б
angle = atan2(A.x - B.x, B.y - A.y)
Чтобы получить угол от точки B до C
angle2 = atan2(B.x - C.x, C.y - B.y)
Answer = 180 + angle2 - angle
If (answer < 0){
return answer + 360
}else{
return answer
}
Я только что использовал этот код в своем недавнем проекте, замените B на P1. Вы можете также удалить "180 +", если хотите
Ну, другие ответы, кажется, охватывают все необходимое, поэтому я хотел бы просто добавить это, если вы используете JMonkeyEngine:
Vector3f.angleBetween(otherVector)
как это то, что я пришел сюда в поисках:)
Atan2 output in degrees
PI/2 +90
| |
| |
PI ---.--- 0 +180 ---.--- 0
| |
| |
-PI/2 +270
public static double CalculateAngleFromHorizontal(double startX, double startY, double endX, double endY)
{
var atan = Math.Atan2(endY - startY, endX - startX); // Angle in radians
var angleDegrees = atan * (180 / Math.PI); // Angle in degrees (can be +/-)
if (angleDegrees < 0.0)
{
angleDegrees = 360.0 + angleDegrees;
}
return angleDegrees;
}
// Angle from point2 to point 3 counter clockwise
public static double CalculateAngle0To360(double centerX, double centerY, double x2, double y2, double x3, double y3)
{
var angle2 = CalculateAngleFromHorizontal(centerX, centerY, x2, y2);
var angle3 = CalculateAngleFromHorizontal(centerX, centerY, x3, y3);
return (360.0 + angle3 - angle2)%360;
}
// Smaller angle from point2 to point 3
public static double CalculateAngle0To180(double centerX, double centerY, double x2, double y2, double x3, double y3)
{
var angle = CalculateAngle0To360(centerX, centerY, x2, y2, x3, y3);
if (angle > 180.0)
{
angle = 360 - angle;
}
return angle;
}
}