Разделение выпуклой оболочки на две отдельные части

Я пытаюсь решить довольно сложную для меня проблему. Я не новичок в программировании, но я не знаю, как решить эту проблему. Ему дается набор точек (точка []) с координатами Xi и Yi в качестве входных данных. Программа должна выводить окружность выпуклой оболочки многоугольника, но если это необходимо, она может разделить оболочку на две части, две отдельные выпуклые оболочки, для каждой из которых будет содержаться несколько точек. Цель этого деления состоит в том, чтобы иметь более короткую окружность (если сумма окружностей этих двух корпусов короче, чем длина окружности одного корпуса; например, две группы точек, удаленных друг от друга). Проблема также в том, что не может быть более двух корпусов. Буду признателен за любые идеи.

Есть простая иллюстрация этой проблемы (может быть гораздо больше точек). Здесь вы можете видеть, что окружность двух отдельных корпусов короче, чем окружность одного.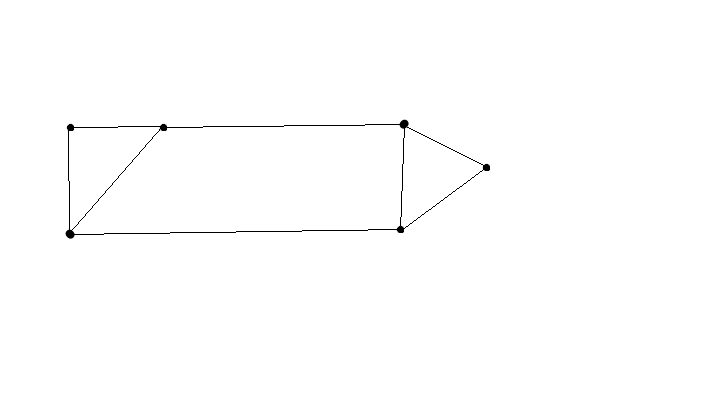

ДОБАВИТЬ: На самом деле под "окружностью" я подразумеваю периметр.

Вот ключевая часть моего кода:

m.x = (a.x + b.x)/2;
    m.y = (a.y + b.y)/2;

    ab.first = b.x - a.x;
    ab.second = b.y - a.y;

    for (i=0; i<n; ++i)
    {
        if (p[i].x * ab.first + p[i].y * ab.second - (SQ(ab.second) + SQ(ab.first))/2 > 0)
            left[l++]=p[i];
        else if (p[i].x * ab.first + p[i].y * ab.second - (SQ(ab.second) + SQ(ab.first))/2 < 0)
            right[r++]=p[i];
        if (p[i].x * ab.first + p[i].y * ab.second - (SQ(ab.second) + SQ(ab.first))/2 == 0)
            mid[md++]=p[i];
    }
Источник

2 ответа

Решение

Кажется, что два корпуса будут полезны, когда существуют два (или более) длинно разделенных кластера. Поэтому я бы предложил попробовать простой метод (вероятно, приблизительный):

construct convex hull
find the farthest pair of points (A, B) in hull with rotating calipers
divide all the points with middle perpendicular to AB segment
find hulls of resulted clouds and calculate profit or loss

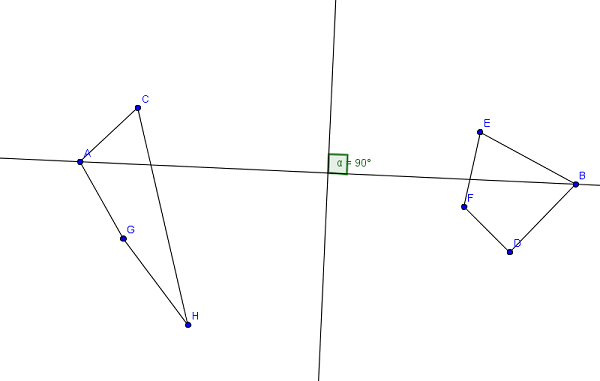
Добавлено: поиск самой дальней пары точек с помощью вращающихся скоб

Добавлено 2: Как разделить облако точек на средний перпендикуляр:

Средняя точка: M = (A + B) / 2
(MX = (AX + BX)/2, MY = (AY + BY)/2)

Вектор AB: (BX-AX, BY-AY)

Средняя перпендикулярная линия имеет общее уравнение:

(y-M.Y) / AB.X = - (x-M.X) / AB.Y
(y-M.Y) * AB.Y + (x-M.X) * AB.X = 0
//incorrect  x * AB.X + y * AB.Y - (AB.Y^2 + AB.X^2)/2 = 0
x * AB.X + y * AB.Y - (B.Y^2 - A.Y^2 + B.X^2 - A.X^2)/2 = 0

Когда вы используете P[i].X и P[i].Y для каждой точки вместо x и y в последнем уравнении, вы получите положительное значение для точек слева и отрицательное значение для точек справа от линии (и нулевое значение для точек на линии)

Источник

Я согласен с MBo, что хитрость заключается в том, чтобы найти широкий интервал, в котором можно разрезать два корпуса. Но я не согласен с тем, что вращение суппортов является правильным подходом. То, что вас волнует, это не внешние измерения, а внутренние измерения. Если у вас очень широкий набор точек, которые организованы в две параллельные горизонтальные линии, вы хотите разрезать между двумя линиями, а не на половине каждой.

По сути, я думаю, что вы хотите найти "толстую" разделительную линию, которая разрезает набор точек на две части и максимально удалена от точек с обеих сторон. Это известно как "самая далекая проблема гиперплоскости" и обычно используется для неконтролируемого варианта алгоритма машины опорных векторов.

Это сложная задача (NP-hard), но существуют алгоритмы аппроксимации. Основная идея состоит в том, чтобы взять много потенциальных углов для линии и выяснить, где поставить линию этого угла, чтобы максимизировать ее разделение.

Источник
Другие вопросы по тегам