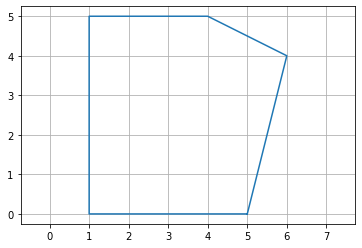
Как определить, находится ли список точек многоугольника по часовой стрелке?
Имея список точек, как мне найти, если они расположены по часовой стрелке?
Например:
point[0] = (5,0)
point[1] = (6,4)
point[2] = (4,5)
point[3] = (1,5)
point[4] = (1,0)
сказал бы, что это против часовой стрелки (или против часовой стрелки, для некоторых людей).
25 ответов
Некоторые из предложенных методов потерпят неудачу в случае невыпуклого многоугольника, такого как полумесяц. Вот простой, который будет работать с невыпуклыми многоугольниками (он даже будет работать с самопересекающимся многоугольником, подобным восьмерке, сообщая вам, в основном ли он по часовой стрелке).
Суммируйте по краям, (x2 - x1) (y2 + y1). Если результат положительный, кривая идет по часовой стрелке, если она отрицательная, кривая против часовой стрелки. (Результат в два раза больше замкнутой области с условием +/-.)
point[0] = (5,0) edge[0]: (6-5)(4+0) = 4
point[1] = (6,4) edge[1]: (4-6)(5+4) = -18
point[2] = (4,5) edge[2]: (1-4)(5+5) = -30
point[3] = (1,5) edge[3]: (1-1)(0+5) = 0
point[4] = (1,0) edge[4]: (5-1)(0+0) = 0
---
-44 counter-clockwise
Найдите вершину с наименьшим y (и наибольшим x, если есть связи). Пусть вершина будет A и предыдущая вершина в списке будет B и следующая вершина в списке будет C, Теперь вычислите знак перекрестного произведения AB а также AC,
Рекомендации:
Как мне найти ориентацию простого многоугольника? в часто задаваемых вопросах: comp.graphics.algorithms.
Кривая ориентации в Википедии.
Я думаю, это довольно старый вопрос, но я все равно собираюсь выкинуть другое решение, потому что оно простое и не математически интенсивное - оно просто использует базовую алгебру. Вычислите подписанную площадь многоугольника. Если оно отрицательное, точки расположены по часовой стрелке, если положительно, они против часовой стрелки. (Это очень похоже на решение Беты.)
Вычислите область со знаком: A = 1/2 * (x1* y2 - x2* y1 + x2* y3 - x3* y2 +... + xn* y1 - x1* yн)
Или в псевдокоде:
signedArea = 0
for each point in points:
x1 = point[0]
y1 = point[1]
if point is last point
x2 = firstPoint[0]
y2 = firstPoint[1]
else
x2 = nextPoint[0]
y2 = nextPoint[1]
end if
signedArea += (x1 * y2 - x2 * y1)
end for
return signedArea / 2
Обратите внимание, что если вы проверяете только порядок, вам не нужно делить на 2.
Перекрестное произведение измеряет степень перпендикулярности двух векторов. Представьте, что каждое ребро вашего многоугольника является вектором в плоскости xy трехмерного (3-D) пространства XYZ. Тогда перекрестным произведением двух последовательных ребер является вектор в направлении z (положительное направление z, если второй сегмент направлен по часовой стрелке, минус направление z, если против часовой стрелки). Величина этого вектора пропорциональна синусу угла между двумя исходными краями, поэтому он достигает максимума, когда они перпендикулярны, и сужается, чтобы исчезнуть, когда края коллинеарны (параллельны).
Итак, для каждой вершины (точки) многоугольника вычислите величину перекрестного произведения двух смежных ребер:
Using your data:
point[0] = (5, 0)
point[1] = (6, 4)
point[2] = (4, 5)
point[3] = (1, 5)
point[4] = (1, 0)
Так обозначьте края какedgeA это сегмент от point0 в point1 а такжеedgeB между point1 в point2
...edgeE находится между point4 а также point0,
Тогда вершина А (point0) находится междуedgeE [От point4 в point0]edgeA [От point0 в `point1'
Эти два ребра сами являются векторами, координаты x и y которых можно определить, вычитая координаты их начальной и конечной точек:
edgeE знак равно point0 - point4 знак равно (1, 0) - (5, 0) знак равно (-4, 0) а такжеedgeA знак равно point1 - point0 знак равно (6, 4) - (1, 0) знак равно (5, 4) а также
И перекрестное произведение этих двух смежных ребер вычисляется с использованием определителя следующей матрицы, которая строится путем помещения координат двух векторов под символами, представляющими три координатные оси (i, j& k). Третья (нулевая)-значная координата существует потому, что концепция кросс-произведения является трехмерной конструкцией, и поэтому мы расширяем эти 2-D векторы в 3-D, чтобы применить кросс-произведение:
i j k
-4 0 0
1 4 0
Учитывая, что все перекрестные произведения дают вектор, перпендикулярный к плоскости умножаемых двух векторов, определитель матрицы выше имеет только k, (или ось Z) компонент.
Формула для расчета величины k или компонент оси Za1*b2 - a2*b1 = -4* 4 - 0* 1 знак равно -16
Величина этого значения (-16)- это мера синуса угла между двумя исходными векторами, умноженная на произведение величин двух векторов.
На самом деле, другая формула для его стоимостиA X B (Cross Product) = |A| * |B| * sin(AB),
Итак, чтобы вернуться к показателю угла, вам нужно разделить это значение, (-16), на произведение величин двух векторов.
|A| * |B| знак равно 4 * Sqrt(17) знак равно 16.4924...
Таким образом, мера греха (AB) = -16 / 16.4924 знак равно -.97014...
Это мера того, изогнулся ли следующий сегмент после вершины влево или вправо, и насколько. Нет необходимости принимать арк-синус. Все, что нас волнует, это его величина и, конечно, его знак (положительный или отрицательный)!
Сделайте это для каждой из 4 других точек по замкнутому пути и сложите значения из этого расчета в каждой вершине.
Если итоговая сумма положительна, вы пошли по часовой стрелке, отрицательно, против часовой стрелки.
Вот простая реализация алгоритма на C#, основанная на этом ответе.
Давайте предположим, что у нас есть Vector тип, имеющий X а также Y свойства типа double,
public bool IsClockwise(IList<Vector> vertices)
{
double sum = 0.0;
for (int i = 0; i < vertices.Count; i++) {
Vector v1 = vertices[i];
Vector v2 = vertices[(i + 1) % vertices.Count]; // % is the modulo operator
sum += (v2.X - v1.X) * (v2.Y + v1.Y);
}
return sum > 0.0;
}
Реализация ответа Шона в JavaScript:
function calcArea(poly) {
if(!poly || poly.length < 3) return null;
let end = poly.length - 1;
let sum = poly[end][0]*poly[0][1] - poly[0][0]*poly[end][1];
for(let i=0; i<end; ++i) {
const n=i+1;
sum += poly[i][0]*poly[n][1] - poly[n][0]*poly[i][1];
}
return sum;
}
function isClockwise(poly) {
return calcArea(poly) > 0;
}
let poly = [[352,168],[305,208],[312,256],[366,287],[434,248],[416,186]];
console.log(isClockwise(poly));
let poly2 = [[618,186],[650,170],[701,179],[716,207],[708,247],[666,259],[637,246],[615,219]];
console.log(isClockwise(poly2));Уверен, что это правильно. Кажется, это работает:-)
Эти полигоны выглядят так, если вам интересно:

Начните с одной из вершин и вычислите угол, образованный каждой стороной.
Первый и последний будут равны нулю (так что пропустите); в остальном синус угла будет задан как произведение произведенных нормализаций на единицу длины (точка [n]-точка [0]) и (точка [n-1]-точка [0]).
Если сумма значений положительна, то ваш многоугольник нарисован против часовой стрелки.
Это реализованная функция для OpenLayers 2. Условие наличия многоугольника по часовой стрелке area < 0Это подтверждается этой ссылкой.
function IsClockwise(feature)
{
if(feature.geometry == null)
return -1;
var vertices = feature.geometry.getVertices();
var area = 0;
for (var i = 0; i < (vertices.length); i++) {
j = (i + 1) % vertices.length;
area += vertices[i].x * vertices[j].y;
area -= vertices[j].x * vertices[i].y;
// console.log(area);
}
return (area < 0);
}
Для чего бы это ни стоило, я использовал этот миксин для расчета порядка намотки приложений Google Maps API v3.
В коде используется побочный эффект областей многоугольника: порядок вершин по часовой стрелке дает положительную область, а порядок вращения тех же вершин против часовой стрелки дает ту же площадь, что и отрицательное значение. Код также использует своего рода частный API в библиотеке геометрии Карт Google. Я чувствовал себя комфортно, используя его - используйте на свой страх и риск.
Пример использования:
var myPolygon = new google.maps.Polygon({/*options*/});
var isCW = myPolygon.isPathClockwise();
Полный пример с юнит-тестами @ http://jsfiddle.net/stevejansen/bq2ec/
/** Mixin to extend the behavior of the Google Maps JS API Polygon type
* to determine if a polygon path has clockwise of counter-clockwise winding order.
*
* Tested against v3.14 of the GMaps API.
*
* @author stevejansen_github@icloud.com
*
* @license http://opensource.org/licenses/MIT
*
* @version 1.0
*
* @mixin
*
* @param {(number|Array|google.maps.MVCArray)} [path] - an optional polygon path; defaults to the first path of the polygon
* @returns {boolean} true if the path is clockwise; false if the path is counter-clockwise
*/
(function() {
var category = 'google.maps.Polygon.isPathClockwise';
// check that the GMaps API was already loaded
if (null == google || null == google.maps || null == google.maps.Polygon) {
console.error(category, 'Google Maps API not found');
return;
}
if (typeof(google.maps.geometry.spherical.computeArea) !== 'function') {
console.error(category, 'Google Maps geometry library not found');
return;
}
if (typeof(google.maps.geometry.spherical.computeSignedArea) !== 'function') {
console.error(category, 'Google Maps geometry library private function computeSignedArea() is missing; this may break this mixin');
}
function isPathClockwise(path) {
var self = this,
isCounterClockwise;
if (null === path)
throw new Error('Path is optional, but cannot be null');
// default to the first path
if (arguments.length === 0)
path = self.getPath();
// support for passing an index number to a path
if (typeof(path) === 'number')
path = self.getPaths().getAt(path);
if (!path instanceof Array && !path instanceof google.maps.MVCArray)
throw new Error('Path must be an Array or MVCArray');
// negative polygon areas have counter-clockwise paths
isCounterClockwise = (google.maps.geometry.spherical.computeSignedArea(path) < 0);
return (!isCounterClockwise);
}
if (typeof(google.maps.Polygon.prototype.isPathClockwise) !== 'function') {
google.maps.Polygon.prototype.isPathClockwise = isPathClockwise;
}
})();
Код C# для реализации ответа LHF:
// https://en.wikipedia.org/wiki/Curve_orientation#Orientation_of_a_simple_polygon
public static WindingOrder DetermineWindingOrder(IList<Vector2> vertices)
{
int nVerts = vertices.Count;
// If vertices duplicates first as last to represent closed polygon,
// skip last.
Vector2 lastV = vertices[nVerts - 1];
if (lastV.Equals(vertices[0]))
nVerts -= 1;
int iMinVertex = FindCornerVertex(vertices);
// Orientation matrix:
// [ 1 xa ya ]
// O = | 1 xb yb |
// [ 1 xc yc ]
Vector2 a = vertices[WrapAt(iMinVertex - 1, nVerts)];
Vector2 b = vertices[iMinVertex];
Vector2 c = vertices[WrapAt(iMinVertex + 1, nVerts)];
// determinant(O) = (xb*yc + xa*yb + ya*xc) - (ya*xb + yb*xc + xa*yc)
double detOrient = (b.X * c.Y + a.X * b.Y + a.Y * c.X) - (a.Y * b.X + b.Y * c.X + a.X * c.Y);
// TBD: check for "==0", in which case is not defined?
// Can that happen? Do we need to check other vertices / eliminate duplicate vertices?
WindingOrder result = detOrient > 0
? WindingOrder.Clockwise
: WindingOrder.CounterClockwise;
return result;
}
public enum WindingOrder
{
Clockwise,
CounterClockwise
}
// Find vertex along one edge of bounding box.
// In this case, we find smallest y; in case of tie also smallest x.
private static int FindCornerVertex(IList<Vector2> vertices)
{
int iMinVertex = -1;
float minY = float.MaxValue;
float minXAtMinY = float.MaxValue;
for (int i = 0; i < vertices.Count; i++)
{
Vector2 vert = vertices[i];
float y = vert.Y;
if (y > minY)
continue;
if (y == minY)
if (vert.X >= minXAtMinY)
continue;
// Minimum so far.
iMinVertex = i;
minY = y;
minXAtMinY = vert.X;
}
return iMinVertex;
}
// Return value in (0..n-1).
// Works for i in (-n..+infinity).
// If need to allow more negative values, need more complex formula.
private static int WrapAt(int i, int n)
{
// "+n": Moves (-n..) up to (0..).
return (i + n) % n;
}
Если вы используете Matlab, функция ispolycw возвращает true, если вершины многоугольника расположены по часовой стрелке.
Как также объяснено в этой статье Википедии Кривая ориентации, учитывая 3 балла p, q а также r на плоскости (то есть с координатами x и y), вы можете вычислить знак следующего определителя
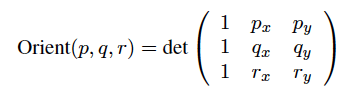
Если определитель является отрицательным (т.е. Orient(p, q, r) < 0), то многоугольник ориентируется по часовой стрелке (CW). Если определитель является положительным (т.е. Orient(p, q, r) > 0), многоугольник ориентирован против часовой стрелки (против часовой стрелки). Определитель равен нулю (т.е. Orient(p, q, r) == 0) если очки p, q а также r коллинеарны.
В приведенной выше формуле мы добавляем перед координатами p, q а также r потому что мы используем однородные координаты.
Вот простая реализация Python 3, основанная на этом ответе (который, в свою очередь, основан на решении, предложенном в принятом ответе)
def is_clockwise(points):
# points is your list (or array) of 2d points.
assert len(points) > 0
s = 0.0
for p1, p2 in zip(points, points[1:] + [points[0]]):
s += (p2[0] - p1[0]) * (p2[1] + p1[1])
return s > 0.0
Другое решение для этого;
const isClockwise = (vertices=[]) => {
const len = vertices.length;
const sum = vertices.map(({x, y}, index) => {
let nextIndex = index + 1;
if (nextIndex === len) nextIndex = 0;
return {
x1: x,
x2: vertices[nextIndex].x,
y1: x,
y2: vertices[nextIndex].x
}
}).map(({ x1, x2, y1, y2}) => ((x2 - x1) * (y1 + y2))).reduce((a, b) => a + b);
if (sum > -1) return true;
if (sum < 0) return false;
}
Возьмите все вершины как массив, как это;
const vertices = [{x: 5, y: 0}, {x: 6, y: 4}, {x: 4, y: 5}, {x: 1, y: 5}, {x: 1, y: 0}];
isClockwise(vertices);
После тестирования нескольких ненадежных реализаций алгоритм, который дал удовлетворительные результаты в отношении ориентации CW/CCW, был опубликован OP в этой теме (shoelace_formula_3).
Как всегда, положительное число представляет ориентацию CW, а отрицательное число - CCW.
Вот быстрое решение 3.0, основанное на ответах выше:
for (i, point) in allPoints.enumerated() {
let nextPoint = i == allPoints.count - 1 ? allPoints[0] : allPoints[i+1]
signedArea += (point.x * nextPoint.y - nextPoint.x * point.y)
}
let clockwise = signedArea < 0
Решение для R, чтобы определить направление и повернуть, если по часовой стрелке (нашел это необходимым для объектов):
coords <- cbind(x = c(5,6,4,1,1),y = c(0,4,5,5,0))
a <- numeric()
for (i in 1:dim(coords)[1]){
#print(i)
q <- i + 1
if (i == (dim(coords)[1])) q <- 1
out <- ((coords[q,1]) - (coords[i,1])) * ((coords[q,2]) + (coords[i,2]))
a[q] <- out
rm(q,out)
} #end i loop
rm(i)
a <- sum(a) #-ve is anti-clockwise
b <- cbind(x = rev(coords[,1]), y = rev(coords[,2]))
if (a>0) coords <- b #reverses coords if polygon not traced in anti-clockwise direction
Мое решение C# / LINQ основано на совете по продуктам @charlesbretana ниже. Вы можете указать эталонную норму для обмотки. Он должен работать до тех пор, пока кривая в основном находится в плоскости, определенной восходящим вектором.
using System.Collections.Generic;
using System.Linq;
using System.Numerics;
namespace SolidworksAddinFramework.Geometry
{
public static class PlanePolygon
{
/// <summary>
/// Assumes that polygon is closed, ie first and last points are the same
/// </summary>
public static bool Orientation
(this IEnumerable<Vector3> polygon, Vector3 up)
{
var sum = polygon
.Buffer(2, 1) // from Interactive Extensions Nuget Pkg
.Where(b => b.Count == 2)
.Aggregate
( Vector3.Zero
, (p, b) => p + Vector3.Cross(b[0], b[1])
/b[0].Length()/b[1].Length());
return Vector3.Dot(up, sum) > 0;
}
}
}
с модульным тестом
namespace SolidworksAddinFramework.Spec.Geometry
{
public class PlanePolygonSpec
{
[Fact]
public void OrientationShouldWork()
{
var points = Sequences.LinSpace(0, Math.PI*2, 100)
.Select(t => new Vector3((float) Math.Cos(t), (float) Math.Sin(t), 0))
.ToList();
points.Orientation(Vector3.UnitZ).Should().BeTrue();
points.Reverse();
points.Orientation(Vector3.UnitZ).Should().BeFalse();
}
}
}
Для тех, кто не хочет «изобретать велосипед», думаю, стоит упомянуть, что эта проверка реализована в красивом пакете Python под названием (github) (который основан на библиотеке GEOS C/C++):
Shapely — это пакет Python под лицензией BSD для управления и анализа плоских геометрических объектов. Он использует широко распространенную библиотеку геометрии с открытым исходным кодом GEOS (движок PostGIS и порт JTS). Shapely объединяет геометрию и операции GEOS, предоставляя как многофункциональный интерфейс Geometry для сингулярных (скалярных) геометрий, так и высокопроизводительные ufuncs NumPy для операций, использующих массивы геометрий. Shapely не ориентирован в первую очередь на форматы сериализации данных или системы координат, но может быть легко интегрирован с другими пакетами.
Источник: Shapelyhttps://shapely.readthedocs.io/en/stable/
Небольшой пример с учетом координат OP:
import numpy as np
from shapely.geometry import Polygon
points = np.array([
(5,0),
(6,4),
(4,5),
(1,5),
(1,0)
])
P = Polygon(points)
Это недавно построенный полигон:
import matplotlib.pyplot as plt
x,y = P.exterior.coords.xy
plt.plot(x,y)
plt.axis('equal')
plt.grid()
plt.show()
И вы можете напрямую использоватьсвойство LinearRing, чтобы проверить, является ли полигон CW или CCW:
type(P.exterior)
>: shapely.geometry.polygon.LinearRing
P.exterior.is_ccw
>: True
Если наоборот:
points = np.flipud(points)
points
>:
array([[1, 0],
[1, 5],
[4, 5],
[6, 4],
[5, 0]])
P1 = Polygon(points)
P1.exterior.is_ccw
>: True
Документация и ссылки для дальнейшего чтения:
стройный
is_ccw(github): https://github.com/shapely/shapely/blob/eba985c6e0170ecdd90c83592fd0afa7ae793cb8/shapely/predicates.py#L72-L108libgeos (github): https://github.com/libgeos/geos
Ссылка на API GEOS: https://libgeos.org/doxygen/classgeos_1_1algorithm_1_1Orientation.html#a5af93795969b80f97d7997195974d7c8
Реализация GEOS (github): https://github.com/libgeos/geos/blob/ab0ce6dafdf7f75ec6d234b6c65bb209037dda17/src/algorithm/Orientation.cpp#L43-L133
Javascript-реализация ответа lhf
(опять же, это работает только для простых многоугольников, а не для восьмерки)
Хотя эти ответы верны, они математически более интенсивны, чем необходимо. Предположим, координаты карты, где самая северная точка является самой высокой точкой на карте. Найдите самую северную точку, и если 2 точки связаны, то это самый северный, а затем самый восточный (это точка, которую lhf использует в своем ответе). В ваших очках,
точка [0] = (5,0)
точка [1] = (6,4)
точка [2] = (4,5)
точка [3] = (1,5)
точка [4] = (1,0)
Если мы предположим, что P2 - самая северная точка, то восточная точка либо предыдущей, либо следующей точки определяет по часовой стрелке, CW или CCW. Поскольку самая северная точка находится на северной стороне, если P1 (предыдущий) к P2 перемещается на восток, направление - CW. В этом случае он движется на запад, поэтому в направлении принятого ответа указано CCW. Если предыдущая точка не имеет горизонтального перемещения, то та же система применяется к следующей точке, P3. Если P3 к западу от P2, это так, тогда движение - это против часовой стрелки. Если движение P2 к P3 - восток, в этом случае это запад, движение CW. Предположим, что nte, P2 в ваших данных, является самой северной, чем восточной точкой, а prv - предыдущей точкой, P1 в ваших данных, а nxt - следующей точкой, P3 в ваших данных, а [0] - горизонтально или восточно / запад, где запад меньше, чем восток, и [1] является вертикальным.
if (nte[0] >= prv[0] && nxt[0] >= nte[0]) return(CW);
if (nte[0] <= prv[0] && nxt[0] <= nte[0]) return(CCW);
// Okay, it's not easy-peasy, so now, do the math
if (nte[0] * nxt[1] - nte[1] * nxt[0] - prv[0] * (nxt[1] - crt[1]) + prv[1] * (nxt[0] - nte[0]) >= 0) return(CCW); // For quadrant 3 return(CW)
return(CW) // For quadrant 3 return (CCW)
Это мое решение, используя объяснения в других ответах:
def segments(poly):
"""A sequence of (x,y) numeric coordinates pairs """
return zip(poly, poly[1:] + [poly[0]])
def check_clockwise(poly):
clockwise = False
if (sum(x0*y1 - x1*y0 for ((x0, y0), (x1, y1)) in segments(poly))) < 0:
clockwise = not clockwise
return clockwise
poly = [(2,2),(6,2),(6,6),(2,6)]
check_clockwise(poly)
False
poly = [(2, 6), (6, 6), (6, 2), (2, 2)]
check_clockwise(poly)
True
Гораздо более простой в вычислительном отношении метод, если вы уже знаете точку внутри многоугольника:
Выберите любой отрезок из исходного многоугольника, точки и их координаты в указанном порядке.
Добавьте известную "внутреннюю" точку и сформируйте треугольник.
Рассчитайте CW или CCW, как предложено здесь, с этими тремя точками.
Я думаю, что для того, чтобы некоторые точки давались по часовой стрелке, все ребра должны быть положительными, а не только сумма ребер. Если одно ребро отрицательно, то по крайней мере 3 очка даются против часовой стрелки.
Найти центр масс этих точек.
Предположим, есть линии от этой точки до ваших точек.
найти угол между двумя линиями для line0 line1
чем сделать это для line1 и line2
...
...
если этот угол монотонно увеличивается, чем против часовой стрелки,
иначе, если монотонно уменьшается, то по часовой стрелке
остальное (не монотонно)
Вы не можете решить, так что это не мудро