Деформированное изображение, появляющееся в цилиндрической проекции

Question

Я хочу деформировать плоское изображение таким образом, чтобы оно представляло собой проекцию, исходящую из цилиндра.

У меня есть плоское изображение, как это:

и я хочу показать это как-то так в 2D-изображении:

Я немного отказался от геометрических проекций. Я посетил некоторые другие вопросы, подобные этому, но я не понимаю, как я буду представлять эти цилиндрические координаты (theta и rho) в координатах x,y в декартовой (x,y) плоскости. Не могли бы вы, ребята, помочь мне с подробным примером? Я пишу код для iPhone и не использую сторонние библиотеки, такие как OpenCV и т. Д.

Огромное спасибо.

Answer 1

Это ответ на 2 части, математика и код

математический

Мне нравится эта проблема, потому что интересная проекция интересна, но математику можно решить вручную без особых сложностей. Для начала важно понять, почему именно изображение искажается так, как оно выглядит. Допустим, перед нами плоское изображение с вогнутым цилиндром.

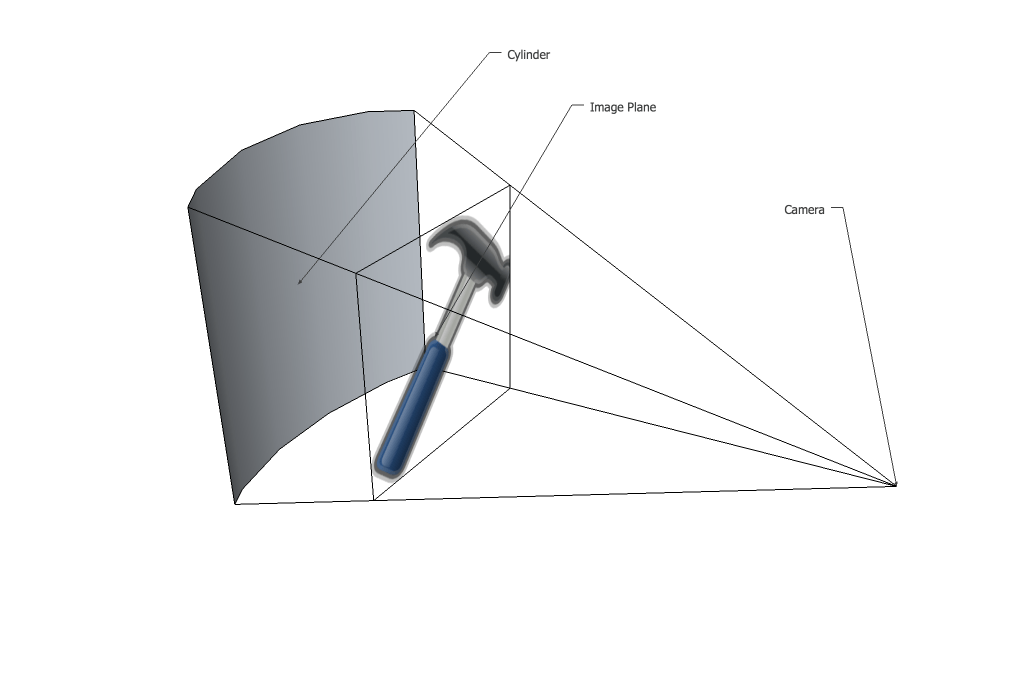
Первым шагом является создание ортографической проекции, перемещающей изображение на искривленную поверхность.

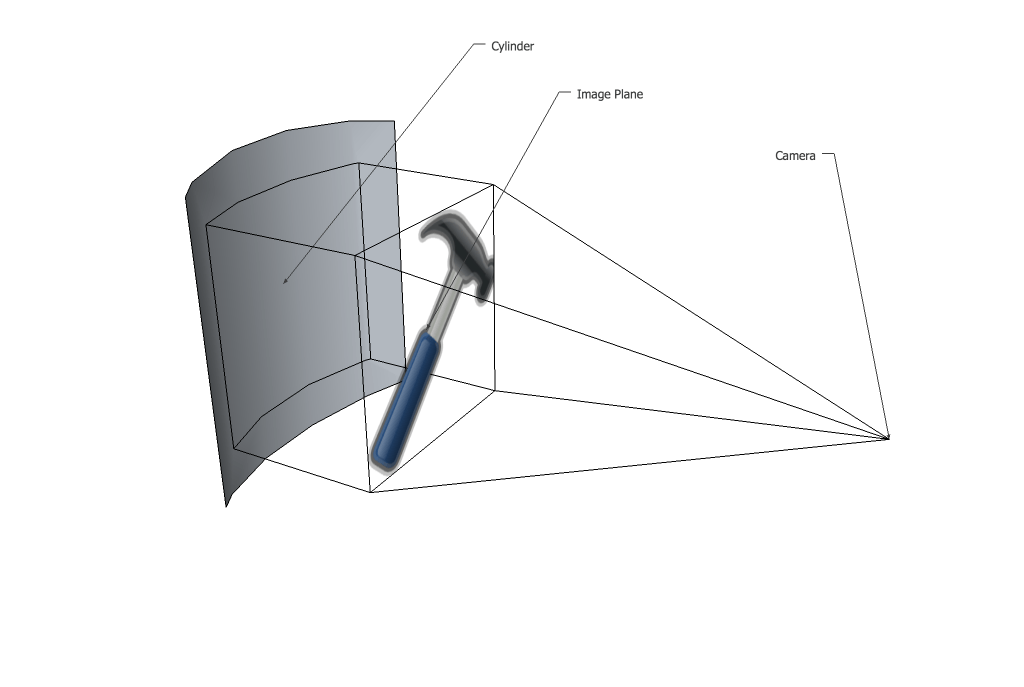
Затем эти точки проецируются с перспективой обратно на плоскость изображения. Обратите внимание, что в этом случае все изображение сжимается, потому что все части цилиндра имели большую координату z, чем плоскость изображения. В вашем случае цилиндр касается плоскости изображения на левом и правом краях, поэтому не происходит усадка. Когда точки проецируются назад, обратите внимание, что они больше не образуют плоскую линию на плоскости изображения, появляется кривая из-за координаты z цилиндра, изменяющейся в зависимости от x.

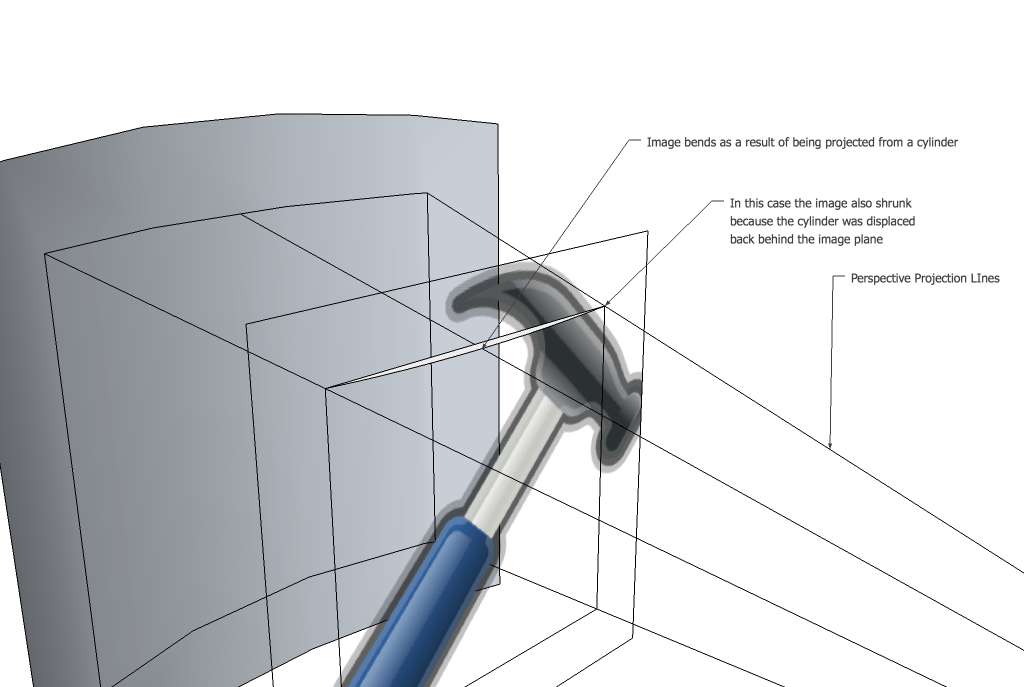
Первый трюк заключается в том, что мы действительно хотим представить этот процесс задом наперед. Сначала вы можете подумать, что хотите взять каждый пиксель исходного изображения и переместить его в новое изображение. Это на самом деле работает намного лучше, если вы проверите каждый пиксель в вашем новом изображении, где он появился на старом изображении, и установите его цвет. Это означает, что вам нужно сделать 3 вещи.

1. Настройте параметры своего цилиндра
2. Спроецируйте луч с камеры, пройдя через каждую точку нового изображения, и найдите его координаты x,y,z на цилиндре.
3. Используйте ортографическую проекцию, чтобы переместить этот луч обратно в плоскость изображения (просто означает падение компонента z)

Отслеживание всего может быть немного сложным, поэтому я попытаюсь использовать последовательную терминологию. Прежде всего, я предполагаю, что вы хотите гарантировать, что ваш цилиндр касается вашего изображения по краям. Если это так, то вы можете выбрать 2 свободных параметра: радиус цилиндра и фокусное расстояние.

Уравнение окружности в плоскости zx имеет вид

x^2+(z-z0)^2 = r^2

предполагая, что центр круга лежит на оси Z. Если край цилиндра будет касаться края плоскости изображения, которая имеет ширину w и фокусное расстояние f, то

omega^2+(f-z0)^2 = r^2 //define omega = width/2, it cleans it up a bit
z0 = f-sqrt(r^2-omega^2)

Теперь мы знаем все параметры цилиндра, который мы переходим к шагу 2, проецируем линии от камеры через плоскость изображения в xim к цилиндру в xc. Вот краткая схема терминологии.

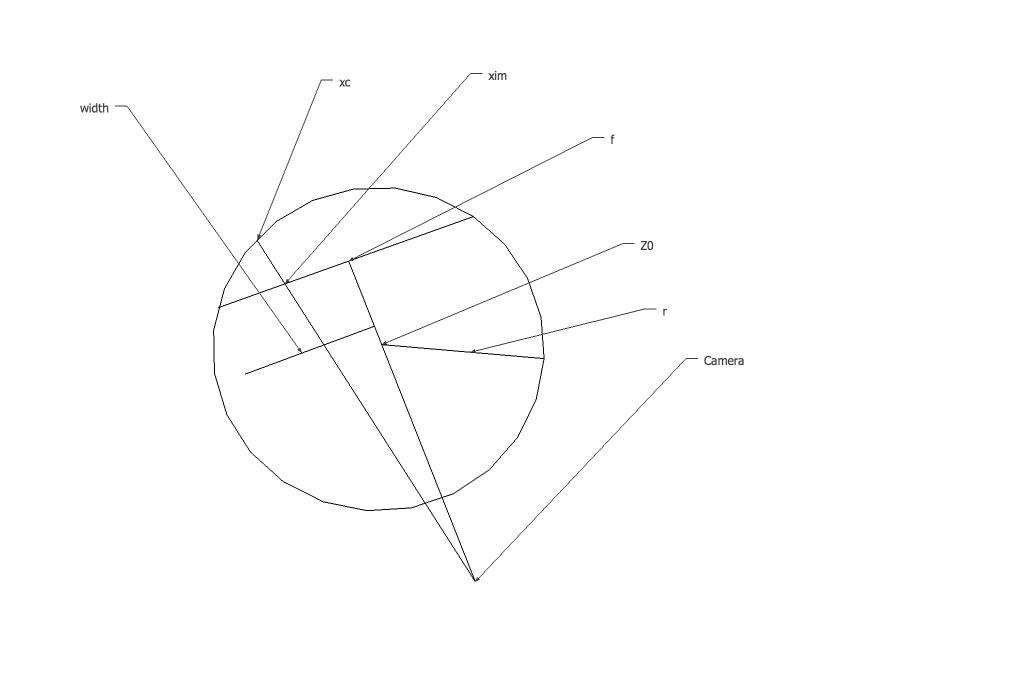
Мы знаем, что проецируемая линия начинается в начале координат и пересекает плоскость изображения в xim. Мы можем написать его уравнение как

x = xim*z/f

Поскольку мы хотим, чтобы координата х, когда он проходит через цилиндр, объединить уравнения

xim^2*z^2/f^2 + z^2 - 2*z*z0 +z0^2 - r^2 = 0

Вы можете использовать квадратное уравнение, чтобы решить для z, а затем снова подключиться к уравнению линии, чтобы получить х. Эти два решения соответствуют двум местам, где линия касается окружности, поскольку нас интересует только то, что происходит после плоскости изображения, и это всегда будет иметь большую координату x, используйте -b + sqrt(...), затем

xc = xim*z/f;
yc = yim*z/f;

Последний шаг удаления ортогональной проекции - это просто, просто отбросьте компонент z, и все готово.

Код

Я знаю, что вы сказали, что не используете openCV, но я собираюсь использовать его в своей демонстрации в качестве контейнера изображений. Все операции выполняются на попиксельной основе, поэтому вам не составит труда преобразовать их в любой контейнер изображений, который вы используете. Сначала я сделал функцию, которая преобразует координаты изображения в конечном изображении в координаты исходного изображения. OpenCV помещает источник изображения в верхнем левом углу, поэтому я начинаю с вычитания w/2 и h/2 и заканчиваю добавлением их обратно в

cv::Point2f convert_pt(cv::Point2f point,int w,int h)
{
//center the point at 0,0
cv::Point2f pc(point.x-w/2,point.y-h/2);

//these are your free parameters
float f = w;
float r = w;

float omega = w/2;
float z0 = f - sqrt(r*r-omega*omega);

float zc = (2*z0+sqrt(4*z0*z0-4*(pc.x*pc.x/(f*f)+1)*(z0*z0-r*r)))/(2* (pc.x*pc.x/(f*f)+1)); 
cv::Point2f final_point(pc.x*zc/f,pc.y*zc/f);
final_point.x += w/2;
final_point.y += h/2;
return final_point;
}

Теперь осталось только сэмплировать каждую точку нового изображения на старом. Есть много способов сделать это, и я делаю самый простой из известных мне, билинейная интерполяция. Кроме того, это настроено только для работы с оттенками серого, поэтому сделать так, чтобы оно работало с цветом, просто применить процесс ко всем 3 каналам. Я просто подумал, что так будет яснее.

for(int y = 0; y < height; y++)
{
    for(int x = 0; x < width; x++)
    {
        cv::Point2f current_pos(x,y);
        current_pos = convert_pt(current_pos, width, height);

        cv::Point2i top_left((int)current_pos.x,(int)current_pos.y); //top left because of integer rounding

        //make sure the point is actually inside the original image
        if(top_left.x < 0 ||
           top_left.x > width-2 ||
           top_left.y < 0 ||
           top_left.y > height-2)
        {
            continue;
        }

        //bilinear interpolation
        float dx = current_pos.x-top_left.x;
        float dy = current_pos.y-top_left.y;

        float weight_tl = (1.0 - dx) * (1.0 - dy);
        float weight_tr = (dx)       * (1.0 - dy);
        float weight_bl = (1.0 - dx) * (dy);
        float weight_br = (dx)       * (dy);

        uchar value =   weight_tl * image.at<uchar>(top_left) +
        weight_tr * image.at<uchar>(top_left.y,top_left.x+1) +
        weight_bl * image.at<uchar>(top_left.y+1,top_left.x) +
        weight_br * image.at<uchar>(top_left.y+1,top_left.x+1);

        dest_im.at<uchar>(y,x) = value;
    }
}

Вот пример вывода для f = w/2 и r = w.