Тесселяция круга в OpenGL

Question

У меня проблемы с пониманием математики этой функции. Я хотел бы услышать логику формул (особенно что это за тангенциальный и радиальный фактор), написанных здесь, чтобы создать точки, которые позже (когда он отправляет массив vec3 в функцию) образуют круг в OpenGL.

void doTesselate(const Arc& arc, int slices, std::vector<glm::vec3>& vertices)
{
  double dang = (arc.endAngle() - arc.startAngle()) * Deg2Rad;

  double radius = arc.radius();
  double angIncr = dang / slices;

  double tangetial_factor = tan(angIncr);
  double radial_factor = 1 - cos(angIncr);

  double startAngle = arc.startAngle() * Deg2Rad;
  const glm::vec3& center = arc.center();

  double x = center.x - radius * cos(startAngle);
  double y = center.y - radius * sin(startAngle);

  ++slices;
  for (int ii = 0; ii < slices; ii++) {
    vertices.push_back(glm::vec3(x, y, center.z));

    double tx = center.y - y;
    double ty = x - center.x;

    x += tx * tangetial_factor;
    y += ty * tangetial_factor;

    double rx = center.x - x;
    double ry = center.y - y;

    x += rx * radial_factor;
    y += ry * radial_factor;
  }
}

Answer 1

Идея заключается в следующем:

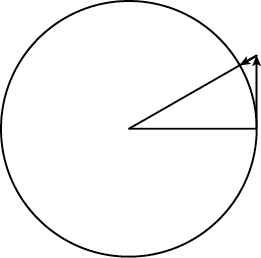
Начиная с текущей точки, вы идете немного в тангенциальном направлении и затем возвращаетесь к центру.

Вектор (tx, ty) является касательной в текущей точке с длиной, равной радиусу. Чтобы добраться до нового угла, нужно двигаться tan(angle) * radius по касательной. radius уже включены в касательный вектор и tan(angle) это tangetial_factor (вы получаете это непосредственно из определения тангенса).

После этого, (rx, ry) вектор к центру Этот вектор имеет длину l:

cos(angle) = radius / l
l = radius / cos(angle)

Нам нужно найти несколько m этого вектора, так что исправленная точка снова лежит на окружности с заданным радиусом. Если мы просто проверим длину, то мы хотим найти:

target distance = current distance    - m * length of (rx, ry)
         radius = radius / cos(angle) - m * radius / cos(angle)
              1 = (1 - m) / cos(angle)
     cos(angle) = 1 - m
 1 - cos(angle) = m

И этот кратный точно radial_factor (количество, которое вам нужно переместить к центру, чтобы попасть на круг).