Построение дерева квадрантов таким образом, что существует только одна разница уровней между соседними узлами (LOD)

Question

Я пытаюсь построить квадродерево, которое делит регион на основе позиции и максимальной глубины. Я хочу использовать это для реализации уровня детализации на местности. Другими словами, у меня есть позиция (x, y), область (x, y, ширина), и я передаю ее в метод сборки (region, position, maxDepth), который затем должен возвращать массив узлов, которые покрывают весь самолет.

Моя реализация немного отличается от этого тем, что глубина, а корневая область представлена ​​объектом Quadtree. Чтобы получить общее подразделение, затем вызывается метод-член get(x, y, radius), который затем возвращает массив узлов, которые покрывают всю корневую область (проверьте код внизу).

Чтобы избежать появления артефактов, для меня важно, чтобы между соседними узлами был максимум 1 уровень.

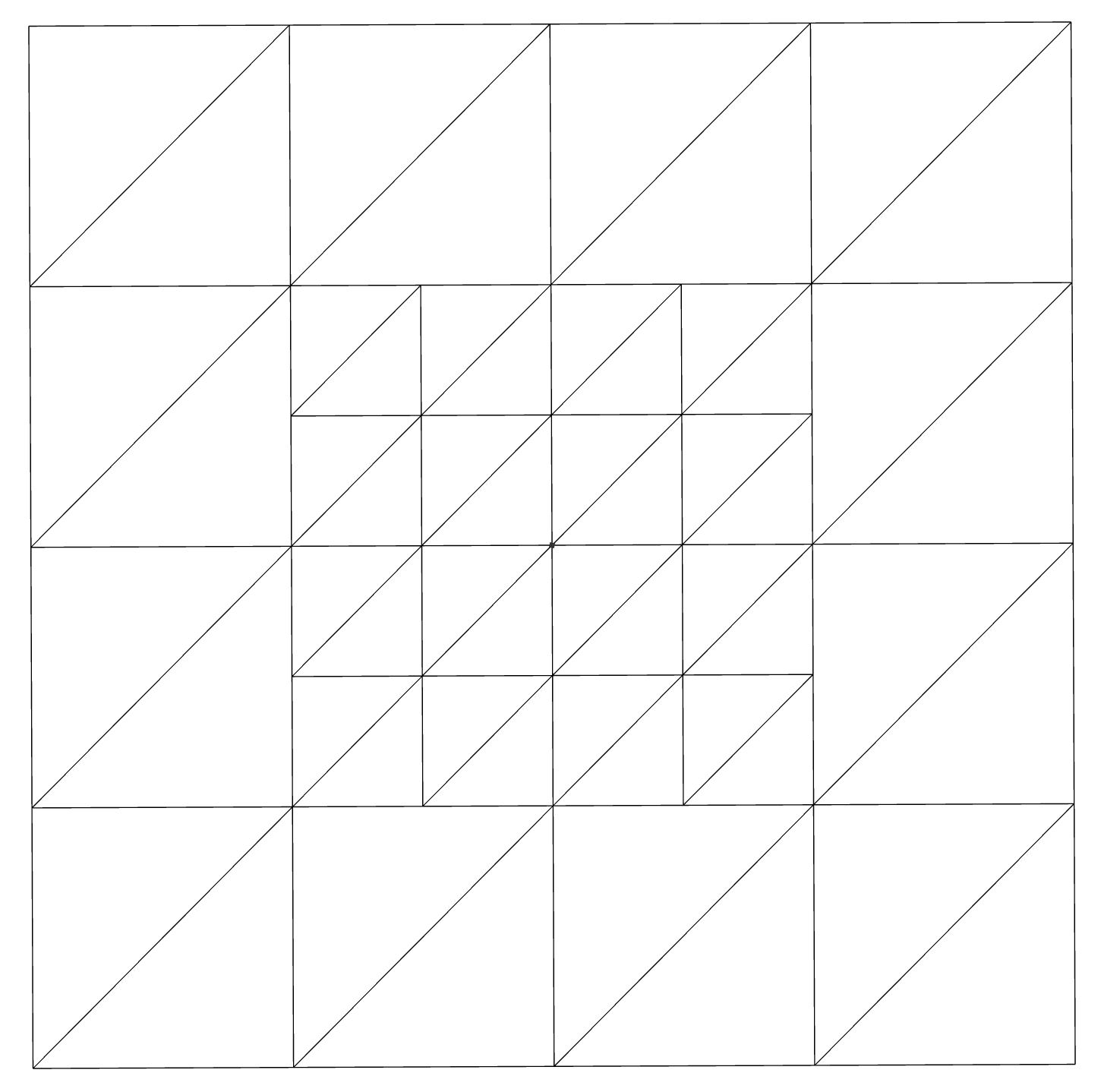
Ниже приведен пример приемлемого результата. Самое большое различие между соседними узлами - 1. (Вы можете игнорировать диагональные линии, они просто являются результатом триангуляции)

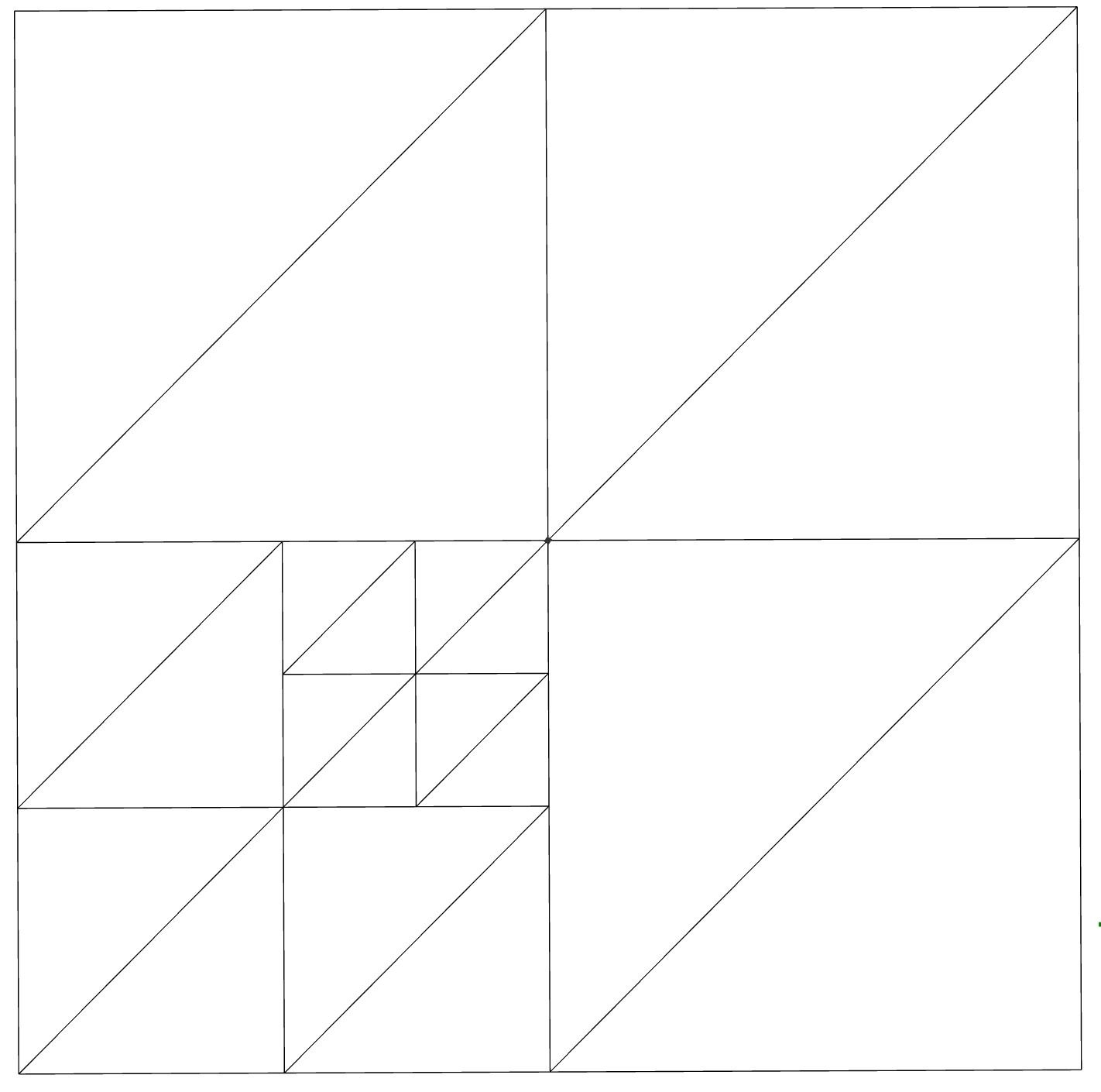
Это, с другой стороны, неприемлемо, поскольку между тремя соседними узлами существует разность 2.

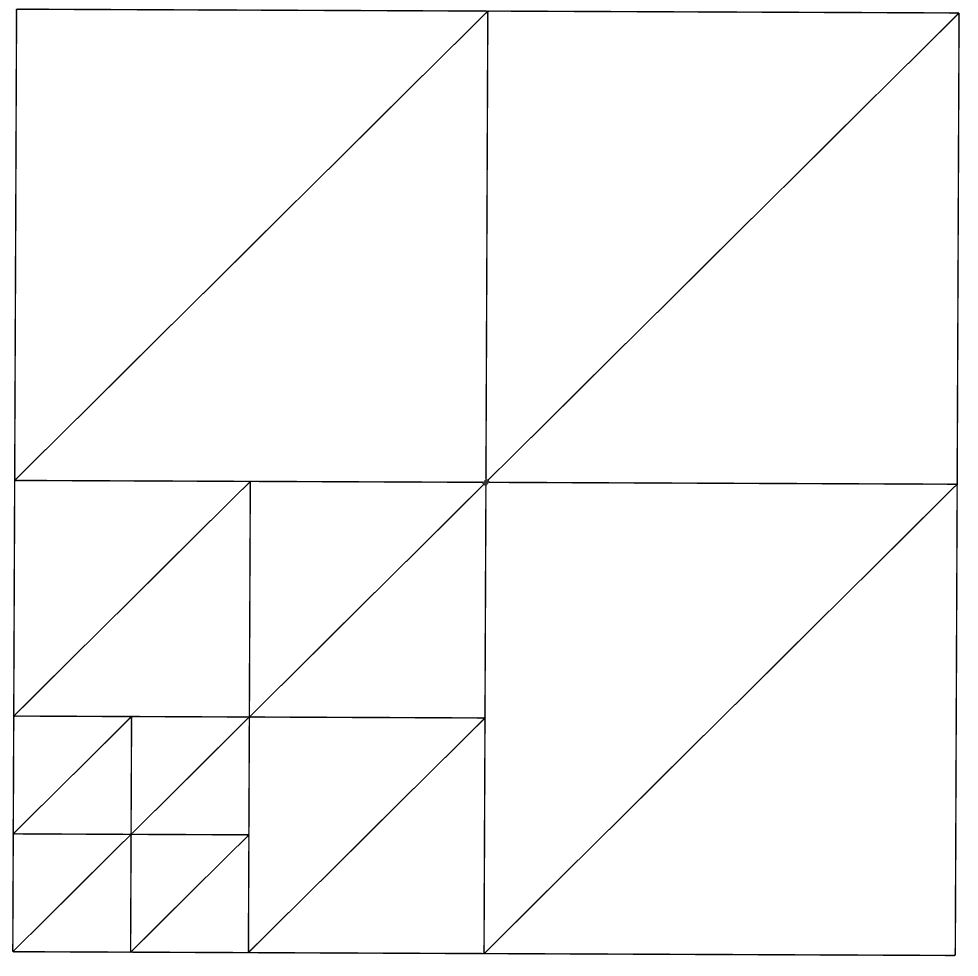
Чтобы это исправить, нам нужно разделить соседние узлы следующим образом:

Еще один пример приемлемого решения будет следующим:

Это код, который у меня есть на данный момент.

class Quadtree {

    constructor({ x, y, width }, levels = 6, parent = null) {

        this.x = x;
        this.y = y;
        this.width = width;

        this.parent = parent;
        this.children = null;

        if (levels > 0) {
            this.children = this.constructor.split(this, levels); // recursively split quadtree.
        }
    }

    /**
     * Checks for intersection.
     * @param  {x, y, radius} circle
     * @param  {x, y, width} square
     * @return {boolean}
     */
    static intersects(circle, square) {
        let deltaX = circle.x - Math.max(square.x, Math.min(circle.x, square.x + square.width));
        let deltaY = circle.y - Math.max(square.y, Math.min(circle.y, square.y + square.width));

        return (deltaX * deltaX + deltaY * deltaY) < (circle.radius * circle.radius);
    }

    /**
     * Splits a node.
     */
    static split(node, levels) {
        let width = node.width / 2;
        let x = node.x;
        let y = node.y;

        // bottom left
        let q1 = new Quadtree({
            x: x,
            y: y,
            width
        }, levels - 1, node);

        // bottom right
        let q2 = new Quadtree({
            x: x + width,
            y: y,
            width
        }, levels - 1, node);

        // top left
        let q3 = new Quadtree({
            x: x,
            y: y + width,
            width
        }, levels - 1, node);

        // top right
        let q4 = new Quadtree({
            x: x + width,
            y: y + width,
            width
        }, levels - 1, node);

        return [q1, q2, q3, q4];
    }

    /**
     * Gets the least amount of nodes covered by the given circle.
     * @param  {x, y, radius} circle
     * @return {Array} An array of Quadtree-nodes.
     */
    get(circle) {

        if (this.children !== null && this.constructor.intersects(circle, { x: this.x, y: this.y, width: this.width })) { // we need to go deeper.
            return this.children.reduce((arr, child) => {

                return arr.concat(child.get(circle));

            }, []);

        } else {
            return [ this ];
        }
    }
}

Вот пример того, как я бы использовал это:

let tree = new Quadtree({ x: 0, y: 0, width: 100}, 2);
let nodes = tree.get({x: 15, y: 15, radius: 5}); // returns an array of nodes covering the whole region.

Примеры:

tree.get({x: -15, y: -15, radius: 5});
[ Quadtree { x: 0, y: 0, width: 100 } ] // returns the top node.

tree.get({x: 15, y: 15, radius: 5});
[ 7 Quadtree-nodes ]

Последний пример возвращает семь узлов Quadtree, например:

#-------#-------#
|       |       |
|       |       |
|       |       |
#---#---#-------#
|   |   |       |
#---#---|       |
|   |   |       |
#---#---#-------#

Если это полезно, то Quadtree-узлы также хранят указатель на своих родителей.

Я иду на это в неправильном направлении? Выполнение ограничений путем возврата к дереву и отслеживания позиций, а что нет, кажется мне слишком сложным. Здесь есть другой угол?

Answer 1

Можно гарантировать, что никакие два соседних узла не удалены более чем на два уровня друг от друга, лишь с небольшой модификацией алгоритма. Идея состоит в том, чтобы разделить узел, когда есть пересечение между кругом и определенным прямоугольником, размеры которого зависят от квадрата узла, а также его глубины.

Подумайте, что влияет на необходимость разделения узла на заданной глубине, начиная с самого глубокого уровня вверх.

1. Узел максимальной глубины не может быть разделен.

2. Узел глубины maxDepth - 1 следует разделять, только если он пересекает круг.

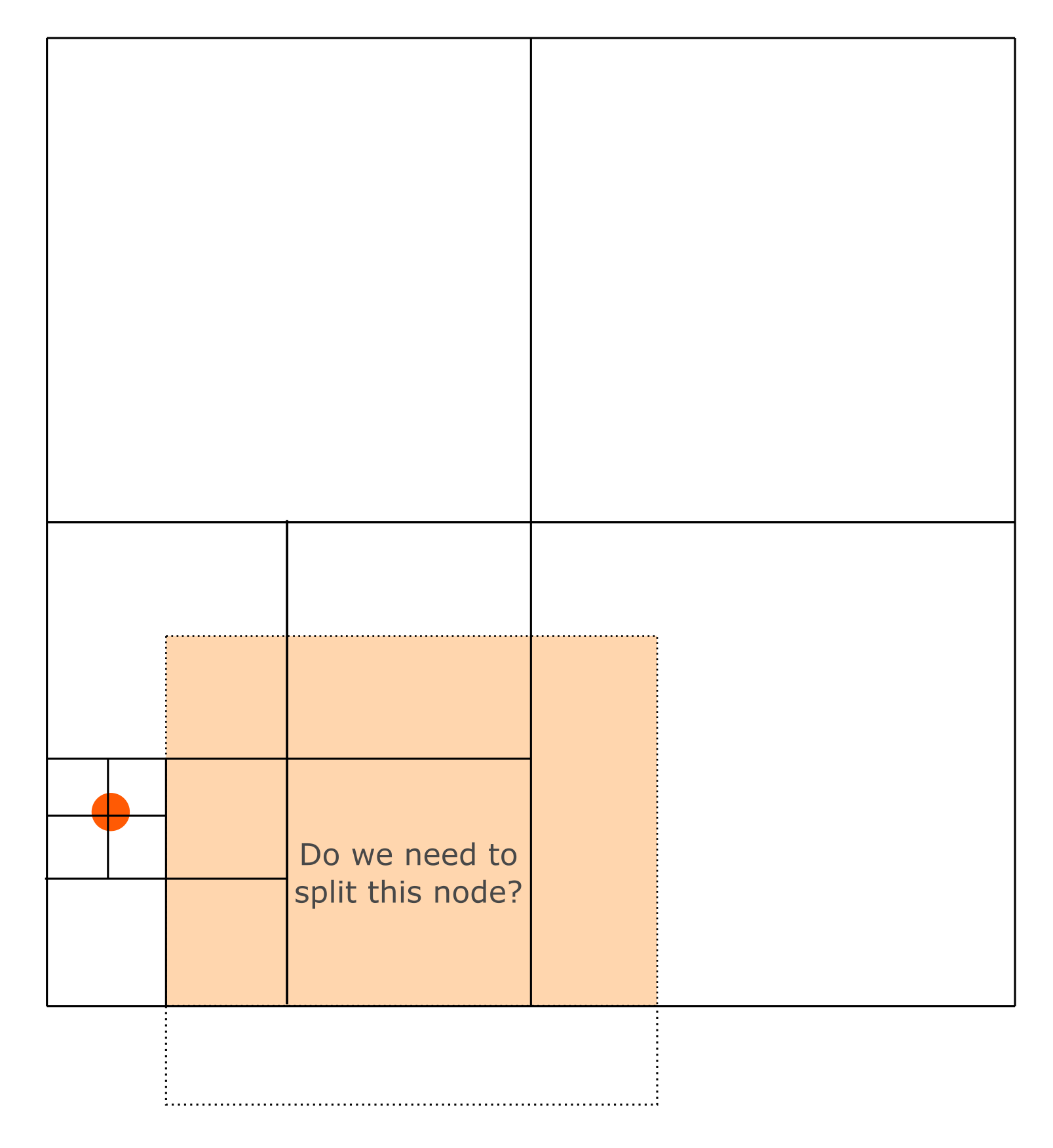
3. Узел глубины maxDepth - 2 должен быть разделен, если он либо пересекает круг, либо примыкает к узлу глубины maxDepth(поэтому сохранение его неразделенным нарушит требование). Но последнее условие равносильно нахождению рядом с узлом глубиныmaxDepth - 1это было разделено. Что, в свою очередь, эквивалентно наличию соседнего узла глубиныmaxDepth - 1который пересекает круг (см. предыдущий абзац). Как определить, так ли это, без обхода соседних узлов и обратного отслеживания? Обратите внимание, что объединение текущего узла(x, y, x + width, y + width) а все его соседние узлы на один уровень глубже равны пересечению квадрата (x - width/2, y - width/2, x + width*2, y+width*2)и квадратный корень. Таким образом, все условие сводится к нахождению пересечения между кругом, квадратным корнем и текущим квадратом, увеличенным в два раза. (Смотрите картинку.)

4. Применяя аналогичные рассуждения к следующему уровню, узел (x, y, x + width, y + width) глубины maxDepth - 3 следует разделить, если есть пересечение между кругом, квадратным корнем и квадратом (x - width*3/4, y - width*3/4, x + width*5/2, y + width*5/2).

5. Наконец, обобщая это на узел произвольной глубины, узел (x, y, x + width, y + width) должен быть разделен тогда и только тогда, когда есть пересечение между кругом, квадратным корнем и квадратом (x - width*inflationRatio/2, y - inflationRatio/2, x + width*(1+inflationRatio), y + width*(1+inflationRatio)), где inflationRatio = 2^(2-maxDepth+depth). (Это можно доказать по индукции, где каждый раздутый квадрат равен объединению узла и всех смежных раздутых квадратов на один уровень глубже).