Прогнозирование с помощью Lowess в R (ИЛИ согласование Loess & Lowess)
Я пытаюсь интерполировать / локально экстраполировать некоторые данные о зарплате, чтобы заполнить набор данных.
Вот набор данных и график доступных данных:
experience salary
1: 1 21878.67
2: 2 23401.33
3: 3 23705.00
4: 4 24260.00
5: 5 25758.60
6: 6 26763.40
7: 7 27920.00
8: 8 28600.00
9: 9 28820.00
10: 10 32600.00
11: 12 30650.00
12: 14 32600.00
13: 15 32600.00
14: 16 37700.00
15: 17 33380.00
16: 20 36784.33
17: 23 35600.00
18: 25 33590.00
19: 30 32600.00
20: 31 33920.00
21: 35 32600.00
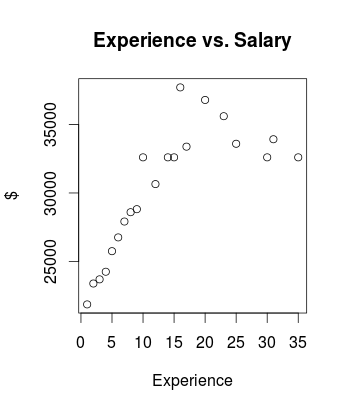
Учитывая явную нелинейность, я надеюсь, что интерполировать и экстраполировать (я хочу заполнить опыт для лет от 0 до 40) через локальную линейную оценку, поэтому я по умолчанию lowess, что дает это:
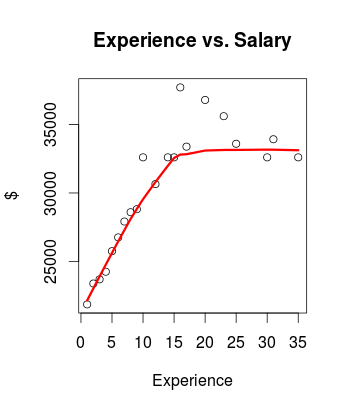
Это хорошо на графике, но исходные данные отсутствуют - графическое устройство R заполнило пробелы для нас. Я не смог найти predict Метод для этой функции, как кажется R движется к использованию loessчто, как я понимаю, является обобщением.
Тем не менее, когда я использую loess (настройка surface="direct" чтобы иметь возможность экстраполировать, как указано в ?loess), который имеет стандарт predict Методом подгонка менее удовлетворительная:
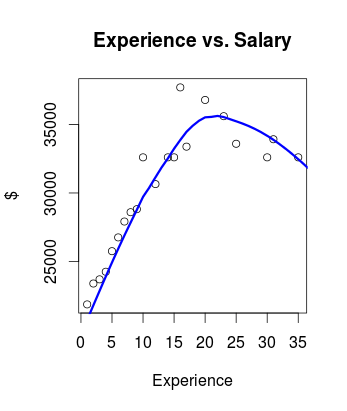
(Есть веские теоретические причины, чтобы сказать, что зарплата не должна уменьшаться - здесь есть некоторый шум / возможное неправильное измерение, определяющее форму буквы U)
И я не могу, кажется, быть в состоянии возиться с любым из параметров, чтобы вернуть неубывающую подгонку, заданную lowess,
Любые предложения, что делать?
1 ответ
Я не знаю, как "согласовать" эти две функции, но я использовал cobs пакет (Непараметрические регрессионные квантили B-сплайнов) с некоторым успехом для подобных задач. Квантиль по умолчанию - это (локальный) медиана или квантиль 0,5. В этом наборе данных выбор по умолчанию для диапазона или ширины ядра кажется очень подходящим.
require(cobs)
Loading required package: cobs
Package cobs (1.3-0) attached. To cite, see citation("cobs")
Rbs <- cobs(x=dat$experience,y=dat$salary, constraint= "increase")
qbsks2():
# Performing general knot selection ...
#
# Deleting unnecessary knots ...
Rbs
#COBS regression spline (degree = 2) from call:
# cobs(x = dat$experience, y = dat$salary, constraint = "increase")
#{tau=0.5}-quantile; dimensionality of fit: 5 from {5}
#x$knots[1:4]: 0.999966, 5.000000, 15.000000, 35.000034
plot(Rbs, lwd = 2.5)
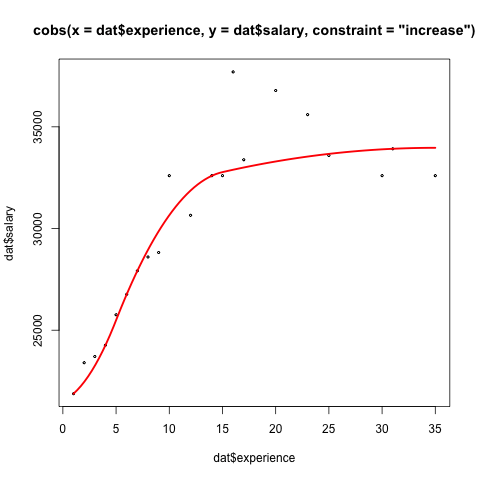
У него есть метод предикторов, хотя вам нужно будет использовать уникальные аргументы, поскольку он не поддерживает обычные data= формализм:
help(predict.cobs)
predict(Rbs, z=seq(0,40,by=5))
z fit
[1,] 0 21519.83
[2,] 5 25488.71
[3,] 10 30653.44
[4,] 15 32773.21
[5,] 20 33295.84
[6,] 25 33669.14
[7,] 30 33893.12
[8,] 35 33967.78
[9,] 40 33893.12