Использование гауссовой смеси для одномерного массива в python sklearn

Question

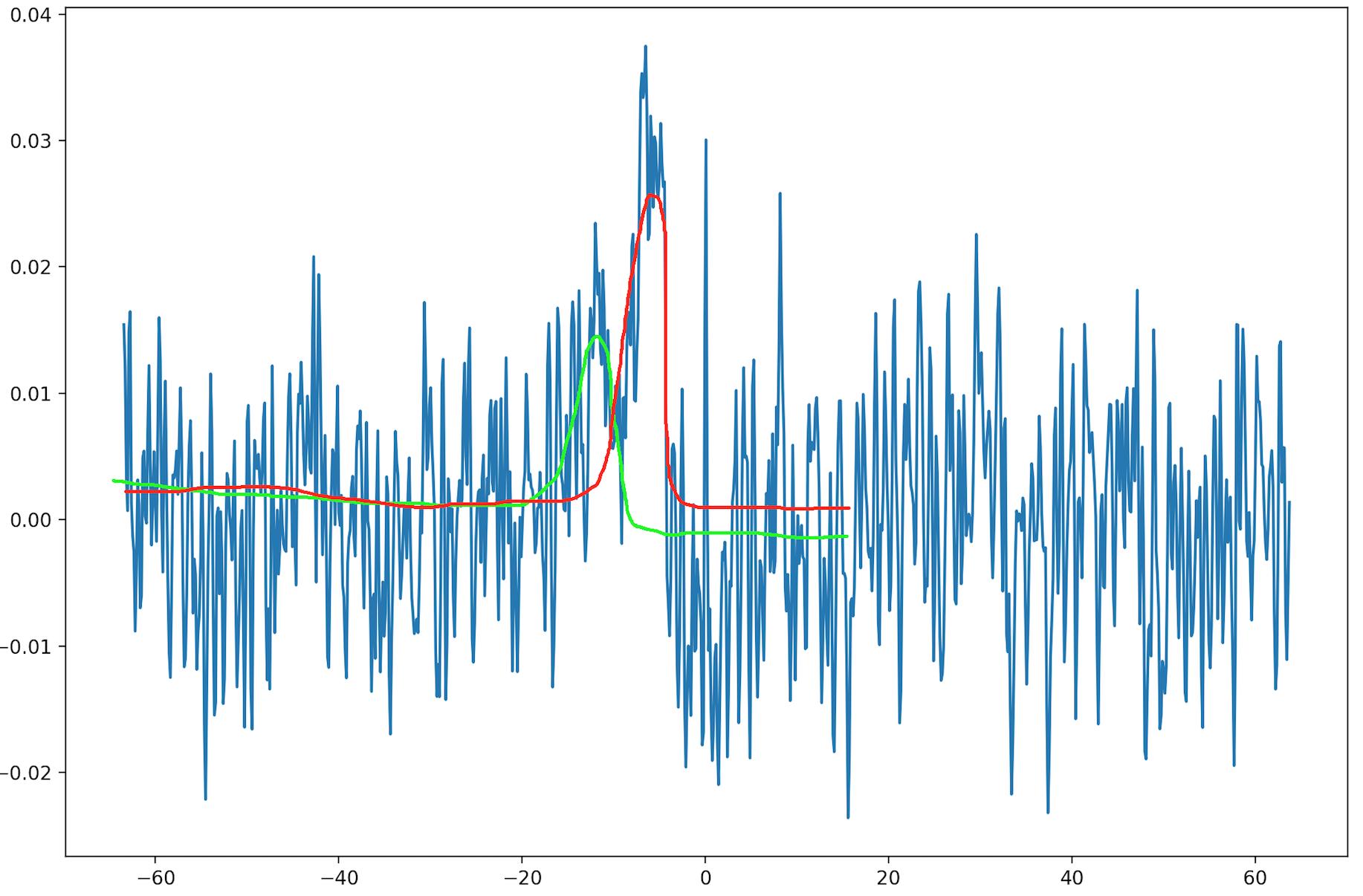
Я хотел бы использовать модель гауссовой смеси, чтобы получить что-то похожее на изображение ниже, кроме правильных гауссиан.

Я пытаюсь использовать питон sklearn.mixture.GaussianMixture но я потерпел неудачу. Я могу рассматривать каждый пик, как если бы он был высотой гистограммы для любого заданного значения x. У меня вопрос: должен ли я найти способ преобразовать этот график в гистограмму и удалить отрицательные значения, или есть ли способ применить GMM непосредственно к этому массиву для получения красных и зеленых гауссианов?

Answer 1

Существует различие между подгонкой кривой для прохождения набора точек с использованием кривой Гаусса и моделированием распределения вероятности некоторых данных с использованием GMM.

Когда вы используете GMM, вы делаете позже, и это не сработает.

• Если вы примените GMM, используя только переменную на оси Y, вы получите гауссово распределение Y, которое не учитывает переменную X.
• Если вы примените GMM, используя 2 переменные, вы получите двумерные гауссианы, которые не помогут вашей проблеме.

Теперь, если вы хотите соответствовать кривой Гаусса. Попробуйте ответить на этот вопрос.

import numpy
from scipy.optimize import curve_fit
import matplotlib.pyplot as plt

# Define some test data which is close to Gaussian
data = numpy.random.normal(size=10000)

hist, bin_edges = numpy.histogram(data, density=True)
bin_centres = (bin_edges[:-1] + bin_edges[1:])/2

# Define model function to be used to fit to the data above:
# Adapt it to as many gaussians you may want
# by copying the function with different A2,mu2,sigma2 parameters
def gauss(x, *p):
    A, mu, sigma = p
    return A*numpy.exp(-(x-mu)**2/(2.*sigma**2))

# p0 is the initial guess for the fitting coefficients (A, mu and sigma above)
p0 = [1., 0., 1.]

coeff, var_matrix = curve_fit(gauss, bin_centres, hist, p0=p0)

# Get the fitted curve
hist_fit = gauss(bin_centres, *coeff)

plt.plot(bin_centres, hist, label='Test data')
plt.plot(bin_centres, hist_fit, label='Fitted data')

# Finally, lets get the fitting parameters, i.e. the mean and standard deviation:
print 'Fitted mean = ', coeff[1]
print 'Fitted standard deviation = ', coeff[2]

plt.show()

Обновление о том, как адаптировать код для нескольких гауссов:

def gauss2(x, *p):
    A1, mu1, sigma1, A2, mu2, sigma2 = p
    return A1*numpy.exp(-(x-mu1)**2/(2.*sigma1**2)) + A2*numpy.exp(-(x-mu2)**2/(2.*sigma2**2))

# p0 is the initial guess for the fitting coefficients initialize them differently so the optimization algorithm works better
p0 = [1., -1., 1.,1., -1., 1.]

#optimize and in the end you will have 6 coeff (3 for each gaussian)
coeff, var_matrix = curve_fit(gauss, X_data, y_data, p0=p0)

#you can plot each gaussian separately using 
pg1 = coeff[0:3]
pg2 = coeff[3:]

g1 = gauss(X_data, *pg1)
g2 = gauss(X_data, *pg2)

plt.plot(X_data, y_data, label='Data')
plt.plot(X_data, g1, label='Gaussian1')
plt.plot(X_data, g2, label='Gaussian2')