Разница между двумя кватернионами
решаемая
Я создаю систему трехмерного портала в моем движке (как игра Portal). Каждый из порталов имеет свою ориентацию, сохраненную в кватернионе. Для рендеринга виртуальной сцены на одном из порталов мне нужно вычислить разницу между двумя кватернионами и использовать результат для поворота виртуальной сцены.
При создании первого портала на левой стене и второго на правой стене вращение от одного к другому будет происходить только по одной оси, но, например, когда первый портал будет создан на полу, а второй - на правой стене вращение от одного к другому может быть в двух осях, и это проблема, потому что вращение идет не так, как надо.
Я думаю, что проблема существует, потому что ориентация, например, X ось и Z Оси хранятся вместе в одном кватернионе, и мне нужно это отдельно, чтобы вручную умножить X * Z (или же Z * X), но как это сделать только с одним кватернионом (разница кватернионов)? Или есть другой способ исправить поворот сцены?
РЕДАКТИРОВАТЬ:
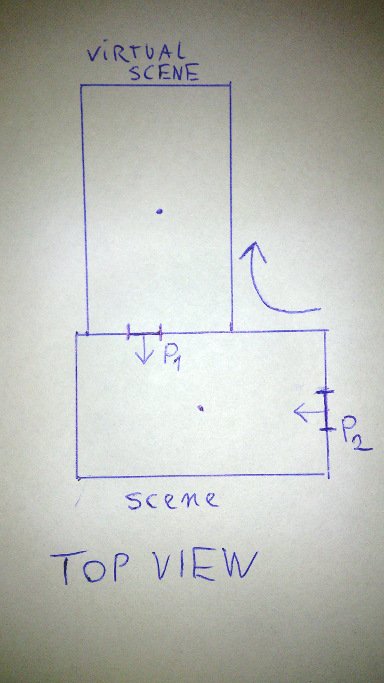
Здесь на этом рисунке два портала P1 и P2, стрелки показывают, как они вращаются. Поскольку я смотрю в P1, я увижу то, что видит P2. Чтобы найти вращение, в котором мне нужно повернуть основную сцену, чтобы она была похожа на виртуальную сцену на этом рисунке, я делаю следующее:
- Получение разности от кватерниона P2 к кватерниону P1
- Результат поворота на 180 градусов по оси Y (портал вверх)
- Использование результата для поворота виртуальной сцены
Этот метод выше работает только тогда, когда разница имеет место только по одной оси. Когда один портал будет находиться на полу или на потолке, это не будет работать, поскольку разностный кватернион встроен в более чем одну ось. Как и предполагалось, я пытался умножить кватернион P1 на кватернион P2, и наоборот, но это не работает.
РЕДАКТИРОВАТЬ 2:
Чтобы найти разницу от P2 до P1, я делаю следующее:
Quat q1 = P1->getOrientation();
Quat q2 = P2->getOrientation();
Quat diff = Quat::diff(q2, q1); // q2 * diff = q1 //
Вот функция Quat::diff:
GE::Quat GE::Quat::diff(const Quat &a, const Quat &b)
{
Quat inv = a;
inv.inverse();
return inv * b;
}
Inverse:
void GE::Quat::inverse()
{
Quat q = (*this);
q.conjugate();
(*this) = q / Quat::dot((*this), (*this));
}
Сопряженные:
void GE::Quat::conjugate()
{
Quat q;
q.x = -this->x;
q.y = -this->y;
q.z = -this->z;
q.w = this->w;
(*this) = q;
}
Скалярное произведение:
float GE::Quat::dot(const Quat &q1, const Quat &q2)
{
return q1.x*q2.x + q1.y*q2.y + q1.z*q2.z + q1.w*q2.w;
}
Оператор *:
const GE::Quat GE::Quat::operator* ( const Quat &q) const
{
Quat qu;
qu.x = this->w*q.x + this->x*q.w + this->y*q.z - this->z*q.y;
qu.y = this->w*q.y + this->y*q.w + this->z*q.x - this->x*q.z;
qu.z = this->w*q.z + this->z*q.w + this->x*q.y - this->y*q.x;
qu.w = this->w*q.w - this->x*q.x - this->y*q.y - this->z*q.z;
return qu;
}
Оператор /:
const GE::Quat GE::Quat::operator/ (float s) const
{
Quat q = (*this);
return Quat(q.x / s, q.y / s, q.z / s, q.w / s);
}
Все это работает, потому что я проверил это с библиотекой GLM
5 ответов
Я решил свою проблему. Как оказалось, мне не нужна разница между двумя поворотами. Просто умножьте одно вращение на 180 градусов, а затем умножьте на обратное значение второго вращения (используя матрицы):
Matrix m1 = p1->getOrientation().toMatrix();
Matrix m2 = p2->getOrientation().toMatrix();
Matrix model = m1 * Matrix::rotation(180, Vector3(0,1,0)) * Matrix::inverse(m2);
и перевод рассчитывается так:
Vector3 position = -p2->getPosition();
position = model * position + p1->getPosition();
model = Matrix::translation(position) * model;
Если вы хотите найти кватернион diff такой, что diff * q1 == q2, тогда вам нужно использовать мультипликативный обратный:
diff * q1 = q2 ---> diff = q2 * inverse(q1)
where: inverse(q1) = conjugate(q1) / abs(q1)
and: conjugate( quaternion(re, i, j, k) ) = quaternion(re, -i, -j, -k)
Если ваши кватернионы являются кватернионами вращения, все они должны быть единичными кватернионами. Это облегчает поиск обратного: abs(q1) = 1, ваш inverse(q1) = conjugate(q1) можно найти, просто отрицая i, j, а также k компоненты.
Однако для описываемого вами вида геометрической конфигурации на основе сцены вы, вероятно, на самом деле не хотите делать это, потому что вам также нужно правильно вычислять перевод.
Самый простой способ сделать все правильно - преобразовать ваши кватернионы в матрицы вращения 4x4 и умножить их в соответствующем порядке с матрицами перевода 4x4, как описано в большинстве вводных текстов компьютерной графики.
Конечно, можно составлять евклидовы преобразования вручную, сохраняя ваши вращения в форме кватернионов, одновременно применяя кватернионы к отдельному вектору трансляции. Однако этот метод технически неясен и склонен к ошибкам кодирования: есть веские причины, по которым форма матрицы 4х4 является обычной, и одна из самых больших заключается в том, что кажется, что так проще сделать это правильно.
Нет, вы должны умножить два кватерниона вместе, чтобы получить последний кватернион, который вы желаете.
Допустим, ваше первое вращение q1 а второй q2, Вы хотите применить их в таком порядке.
Полученный кватернион будет q2 * q1, который будет представлять ваше составное вращение (напомним, что кватернионы используют левое умножение, поэтому q2 применяется к q1 умножением слева)
Для краткого руководства по вычислению одного кватерниона, обратитесь к моему предыдущему ответу переполнения стека
Редактировать:
Чтобы уточнить, вы столкнулись с аналогичной проблемой с матрицами вращения и углами Эйлера. Вы определяете свои преобразования для X, Y и Z, а затем умножаете их вместе, чтобы получить результирующую матрицу преобразования ( вики). У вас та же проблема здесь. Матрицы вращения и кватернионы в большинстве случаев эквивалентны для представления вращений. Кватернионы предпочтительнее в основном потому, что их немного проще представить (и легче решить проблему блокировки карданного подвеса)
Кватернионы работают следующим образом: локальная система отсчета представлена в виде мнимых направлений кватернионов i,j,k. Например, для наблюдателя, стоящего в дверце 1 портала и смотрящего в направлении стрелки, направление i может представлять направление стрелки, j вверх и k=ij указывает справа от наблюдателя. В глобальных координатах, представленных кватернионом q1, оси в трехмерных координатах
q1*(i,j,k)*q1^-1=q1*(i,j,k)*q1',
где q'- сопряженное, а для единичных кватернионов сопряженное - обратное.
Теперь задача состоит в том, чтобы найти единичный кватернион q так, чтобы направления q*(i,j,k)*q'в локальной системе отсчета 1, выраженные в глобальных координатах, совпадали с повернутыми направлениями системы 2 в глобальных координатах. Из эскиза это означает, что вперед становится назад, а слева становится вправо, то есть
q1*q*(i,j,k)*q'*q1'=q2*(-i,j,-k)*q2'
=q2*j*(i,j,k)*j'*q2'
что легко достигается приравниванием
q1*q=q2*j or q=q1'*q2*j.
Но детали могут отличаться, в основном то, что другая ось может представлять направление "вверх" вместо j.
Если глобальная система эскиза находится снизу, так что global-i указывает вперед в вертикальном направлении, global-j вверх и global-k вправо, то local1-(i,j,k) является global-(-i,j,-k), давая
q1=j.
local2-(i,j,k) является глобальным -(-k,j,i), который может быть реализован
q2=sqrt(0.5)*(1+j),
поскольку
(1+j)*i*(1-j)=i*(1-j)^2=-2*i*j=-2*k and
(1+j)*k*(1-j)=(1+j)^2*k= 2*j*k= 2*i
Сравнение этого с фактическими значениями в вашей реализации покажет, как следует изменить назначение осей и направлений кватернионов.
Проверьте https://www.emis.de/proceedings/Varna/vol1/GEOM09.pdf
Представьте себе, чтобы получить dQ от Q1 до Q2, я объясню, почему dQ = Q1 * · Q2 вместо Q2 · Q1 *
Это вращает кадр, а не объект. Для любого вектора v в R3 вращательное действие оператора L(v) = Q*·v·Q
Это не Q · v · Q *, которое является действием вращения объекта.
Если вы поворачиваете Q1, затем Q1 *, а затем Q2, вы можете написать (Q1 · Q1 * · Q2) * · v · (Q1 · Q1 * · Q2) = (Q1 * · Q2) * · Q1 * · v · Q1 · (Q1 * · Q2) = dQ * · Q1 * · v · Q1 · dQ
Так что dQ = Q1 * · Q2