GMM - логарифмическое правдоподобие не монотонно

Question

Вчера я реализовал GMM (модель гауссовой смеси), используя алгоритм максимизации ожидания.

Как вы помните, он моделирует некое неизвестное распределение как смесь гауссиан, которые нам нужны для изучения его средних и дисперсионных значений, а также весов для каждого гауссиана.

это математика, стоящая за кодом (это не так уж сложно) http://mccormickml.com/2014/08/04/gaussian-mixture-models-tutorial-and-matlab-code/

это мой код:

import numpy as np
from scipy.stats import multivariate_normal
import matplotlib.pyplot as plt

#reference for this code is http://mccormickml.com/2014/08/04/gaussian-mixture-models-tutorial-and-matlab-code/

def expectation(data, means, covs, priors): #E-step. returns the updated probabilities
    m = data.shape[0]                       #gets the data, means covariances and priors of all clusters
    numOfClusters = priors.shape[0]

    probabilities = np.zeros((m, numOfClusters))
    for i in range(0, m):
        for j in range(0, numOfClusters):
            sum = 0
            for l in range(0, numOfClusters):
                sum += normalPDF(data[i, :], means[l], covs[l]) * priors[l, 0]
            probabilities[i, j] = normalPDF(data[i, :], means[j], covs[j]) * priors[j, 0] / sum

    return probabilities

def maximization(data, probabilities): #M-step. this updates the means, covariances, and priors of all clusters
    m, n = data.shape
    numOfClusters = probabilities.shape[1]

    means = np.zeros((numOfClusters, n))
    covs = np.zeros((numOfClusters, n, n))
    priors = np.zeros((numOfClusters, 1))

    for i in range(0, numOfClusters):
        priors[i, 0] = np.sum(probabilities[:, i]) / m #update priors

        for j in range(0, m): #update means
            means[i] += probabilities[j, i] * data[j, :]

            vec = np.reshape(data[j, :] - means[i, :], (n, 1))
            covs[i] += probabilities[j, i] * np.dot(vec, vec.T) #update covs

        means[i] /= np.sum(probabilities[:, i])
        covs[i] /= np.sum(probabilities[:, i])

    return [means, covs, priors]

def normalPDF(x, mean, covariance): #this is simply multivariate normal pdf
    n = len(x)

    mean = np.reshape(mean, (n, ))
    x = np.reshape(x, (n, ))

    var = multivariate_normal(mean=mean, cov=covariance,)
    return var.pdf(x)


def initClusters(numOfClusters, data): #initialize all the gaussian clusters (means, covariances, priors
    m, n = data.shape

    means = np.zeros((numOfClusters, n))
    covs = np.zeros((numOfClusters, n, n))
    priors = np.zeros((numOfClusters, 1))

    initialCovariance = np.cov(data.T)

    for i in range(0, numOfClusters):
        means[i] = np.random.rand(n) #the initial mean for each gaussian is chosen randomly
        covs[i] = initialCovariance #the initial covariance of each cluster is the covariance of the data
        priors[i, 0] = 1.0 / numOfClusters #the initial priors are uniformly distributed.

    return [means, covs, priors]

def logLikelihood(data, probabilities): #data is our data. probabilities[i, j] = k means probability example i belongs in cluster j is 0 < k < 1
    m = data.shape[0] #num of examples

    examplesByCluster = np.zeros((m, 1))
    for i in range(0, m):
        examplesByCluster[i, 0] = np.argmax(probabilities[i, :])
    examplesByCluster = examplesByCluster.astype(int) #examplesByCluster[i] = j means that example i belongs in cluster j

    result = 0
    for i in range(0, m):
        result += np.log(probabilities[i, examplesByCluster[i, 0]]) #example i belongs in cluster examplesByCluster[i, 0]

    return result

m = 2000 #num of training examples
n = 8 #num of features for each example

data = np.random.rand(m, n)
numOfClusters = 2 #num of gaussians
numIter = 30 #num of iterations of EM
cost = np.zeros((numIter, 1))

[means, covs, priors] = initClusters(numOfClusters, data)

for i in range(0, numIter):
    probabilities = expectation(data, means, covs, priors)
    [means, covs, priors] = maximization(data, probabilities)

    cost[i, 0] = logLikelihood(data, probabilities)

plt.plot(cost)
plt.show()

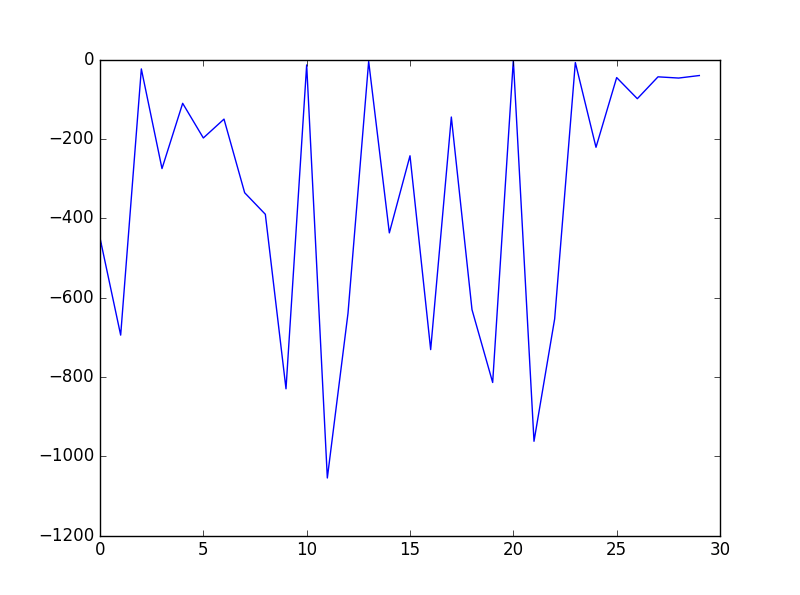
проблема в том, что логарифмическая вероятность ведет себя странно. Я ожидаю, что это будет монотонным увеличением. Но это не так.

Например, с 2000 примерами 8 объектов с 3 гауссовыми кластерами логарифмическое правдоподобие выглядит следующим образом (30 итераций) -

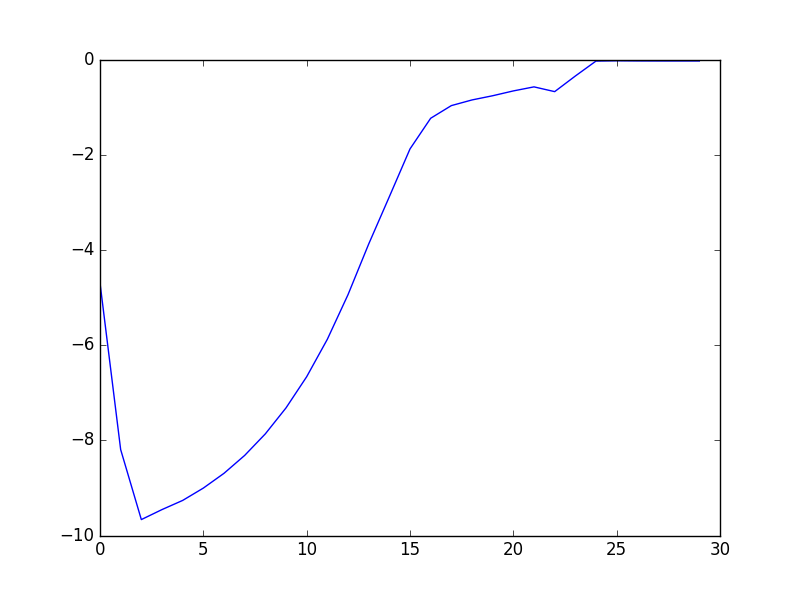
Так что это очень плохо. Но в других тестах, которые я запускал, например, один тест с 15 примерами из 2 функций и 2 кластеров, логарифмическая вероятность такова:

Лучше, но все же не идеально.

Почему это происходит и как я могу это исправить?

Answer 1

Проблема заключается в шаге максимизации.

Код использует means для расчета covs, Однако это делается в том же цикле, прежде чем делить means по сумме вероятностей.

Это приводит к взрыву предполагаемых ковариаций.

Вот предлагаемое исправление:

def maximization(data, probabilities): #M-step. this updates the means, covariances, and priors of all clusters
    m, n = data.shape
    numOfClusters = probabilities.shape[1]

    means = np.zeros((numOfClusters, n))
    covs = np.zeros((numOfClusters, n, n))
    priors = np.zeros((numOfClusters, 1))

    for i in range(0, numOfClusters):
        priors[i, 0] = np.sum(probabilities[:, i]) / m   #update priors

        for j in range(0, m): #update means
            means[i] += probabilities[j, i] * data[j, :]

        means[i] /= np.sum(probabilities[:, i])

    for i in range(0, numOfClusters):
        for j in range(0, m): #update means
            vec = np.reshape(data[j, :] - means[i, :], (n, 1))
            covs[i] += probabilities[j, i] * np.multiply(vec, vec.T) #update covs

        covs[i] /= np.sum(probabilities[:, i])

    return [means, covs, priors]

И полученная функция стоимости (200 точек данных, 4 функции):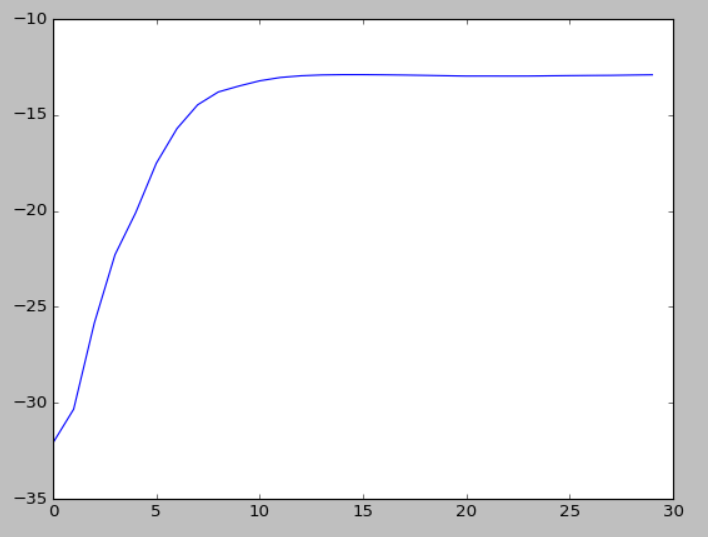

РЕДАКТИРОВАТЬ: я был убежден, что эта ошибка была единственной проблемой в коде, однако, запустив несколько дополнительных примеров, я все еще иногда вижу немонотонное поведение (хотя и менее ошибочное, чем раньше). Так что это, кажется, только часть проблемы.

РЕДАКТИРОВАТЬ 2: Была другая проблема в вычислении ковариации: умножение вектора должно быть поэлементным, а не точечным произведением - имейте в виду, что результатом должен быть вектор. Результаты кажутся постоянно монотонно растущими в настоящее время.