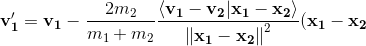Двумерное столкновение с двумя движущимися объектами

Question

Я работаю над двумерным столкновением с двумя движущимися объектами. Это очень просто. У меня есть две сферы, которые имеют разную геометрию и массу. Они сталкиваются под углом 45°. Мне нужно рассчитать векторы скорости обеих сфер после столкновения. Я нашел формулу, которую использовал в википедии, и в этом вопросе: физика двумерного столкновения упругих шаров

Проблема в том, что результирующий импульс отличается от стартового. Начальный - 35 кг м / с, а конечный - 33,75 кг / с. Я посмотрел на доказательство для формулы, она использует сохранение полного импульса, что, вероятно, означает, что изменение общего импульса должно быть равно 0. Моего нет.

Может кто-нибудь объяснить, в чем проблема или что я делаю не так?

Спасибо за ответ.

Я пробовал это в разных случаях много раз, и я всегда немного разочарован в конечном результате.

Мой код:

import numpy as np

v_1 = np.array([3, 0]) #velocity of object 1
v_2 = np.array([0, 2]) #velocity of object 2
r_1 = 0.05 #m ; radius of sphere 1
r_2 = 0.1 #m ; radius of sphere 2
m_1 = 5 #kg ; mass of object 1
m_2 = 10 #kg ; mass of object 2

x_1 = np.array([-(r_1 + r_2)*np.cos(np.pi/4), 0]) #vector of position 1
x_2 = np.array([0, -(r_1 + r_2)*np.cos(np.pi/4)]) #vector of position 2

v_1_p = v_1 - 2*m_2/(m_1 + m_2)*((v_1 - v_2)@(x_1 - x_2))/(np.linalg.norm(x_2 - 
x_1)**2)*(x_1 - x_2) #velocity after colision for object 1 
v_2_p = v_2 - 2*m_1/(m_1 + m_2)*((v_2 - v_1)@(x_2 - x_1))/(np.linalg.norm(x_2 - 
x_1)**2)*(x_2 - x_1) #velocity after colision for object 2

v_1_p_v = np.sqrt(np.sum(v_1_p**2)) #magnitude of velocity 1 
v_2_p_v = np.sqrt(np.sum(v_2_p**2)) #magnitude of velocity 2

p_0 = np.sum(m_1*v_1 + m_2*v_2) #momentum before colision
# value: 35
p_1 = m_1*v_1_p_v + m_2*v_2_p_v #momentum after colision
# value: 33.74652441384409

Я ожидал, что общий импульс до столкновения будет таким же, как и после столкновения.

Answer 1

Проблемы:

1. np.sum(m_1*v_1 + m_2*v_2) не имеет никакого математического смысла, потому что вы добавляете компоненты результирующего вектора импульса, который не равен величине. Измените это на m_1*v_1 + m_2*v_2,

2. m_1*v_1_p_v + m_2*v_2_p_v неверно, потому что вы не можете сложить векторные величины вместе, чтобы получить результирующую векторную величину - ||v1|| + ||v2|| != ||v1 + v2||, Измените это на m_1*v_1_p + m_2*v_2_p,

3. Остерегайтесь целочисленного деления в 2*m_2/(m_1 + m_2), Измените это на (2.0*m_2)/(m_1 + m_2)и аналогично для m_1,