Распределение средств из гамма-распределения не соответствует теоретическим значениям в Python

Question

Я делаю задание для определенного курса на Coursera. Весь смысл в том, чтобы использовать центральную предельную теорему для некоторого распределения (я выбрал гамма-распределение) и построить на диаграмме теоретические значения для функции плотности вероятности нормального распределения с E = Ebase и D = Dbase/n, где E и D - математическое ожидание и дисперсия распределения средств.

Средство взято из выборок размера n, где каждая единица генерируется гамма-распределением с вручную вставленными параметрами (я использую k = 2, theta = 0.5) и поэтому Ebase = k*theta а также Dbase = k*theta^2, На той же диаграмме должна быть гистограмма, нормированная на 1.

Теоретически, чем больше n, тем более подходящими должны быть две графики. Но у меня так в записной книжке ipython:

import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import scipy.stats as sts
%matplotlib inline
k = 2.0
Theta = 0.5
listOfSizes = [20,50,100,300]
number = 0
for n in listOfSizes:
    means =[]
    for i in range (1000):
       sum = 0.0
       for number in np.random.gamma(k,Theta,size = n):
           sum+=number
       mean = sum/n
       means.append(mean)
dispersionOfMeansTheoretical =(k*(Theta**2))/n
mathExpectancyOfMeansTheoretical = (k*Theta)
arguments = np.linspace(0,2,2048)
plt.figure(n)
theoryFunction = sts.norm.pdf(arguments, loc = mathExpectancyOfMeansTheoretical, scale = dispersionOfMeansTheoretical)
plt.plot(arguments, theoryFunction)
plt.hist(means, bins=50, normed = 1)
plt.ylabel('$PDF$ with n ='+str(n))
plt.xlabel('$x$')

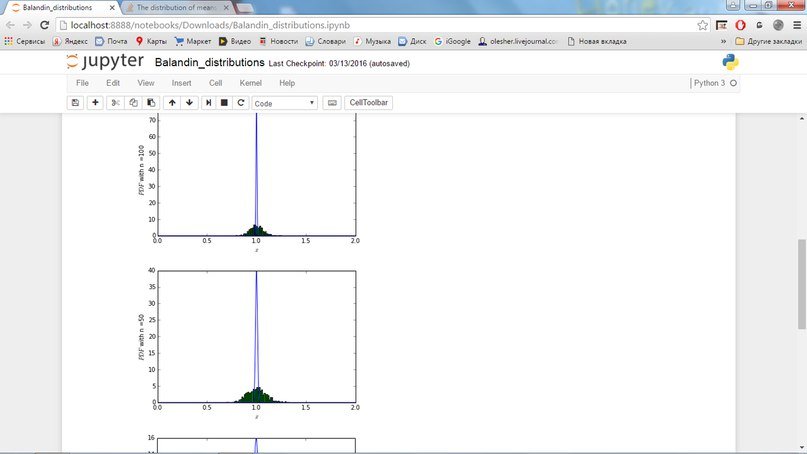
Я дважды проверил это в Wiki, и мне кажется, что я вставил правильную параметризацию для всего, но я действительно не могу найти ошибку. Что я пропустил?