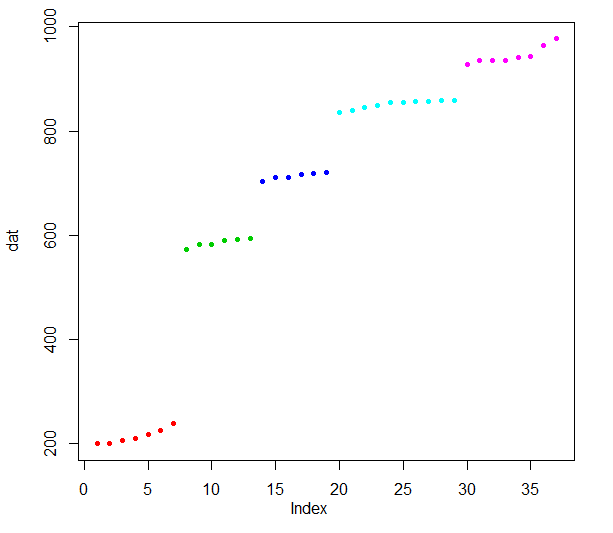
Распознавать уровни данных 1D, зная только количество уровней

Question

Привет, ребята, у меня есть датчик, который выводит данные состоит из одного атрибута (моно значение). Пример набора последовательных данных выглядит следующим образом:

образец: 199 200 205 209 217 224 239 498 573 583 583 590 591 594 703 710 711 717 719 721 836 840 845 849 855 855 856 857 858 858 928 935 936 936 942 943 964 977 977

Вы можете увидеть данные с первого ввода изображения. 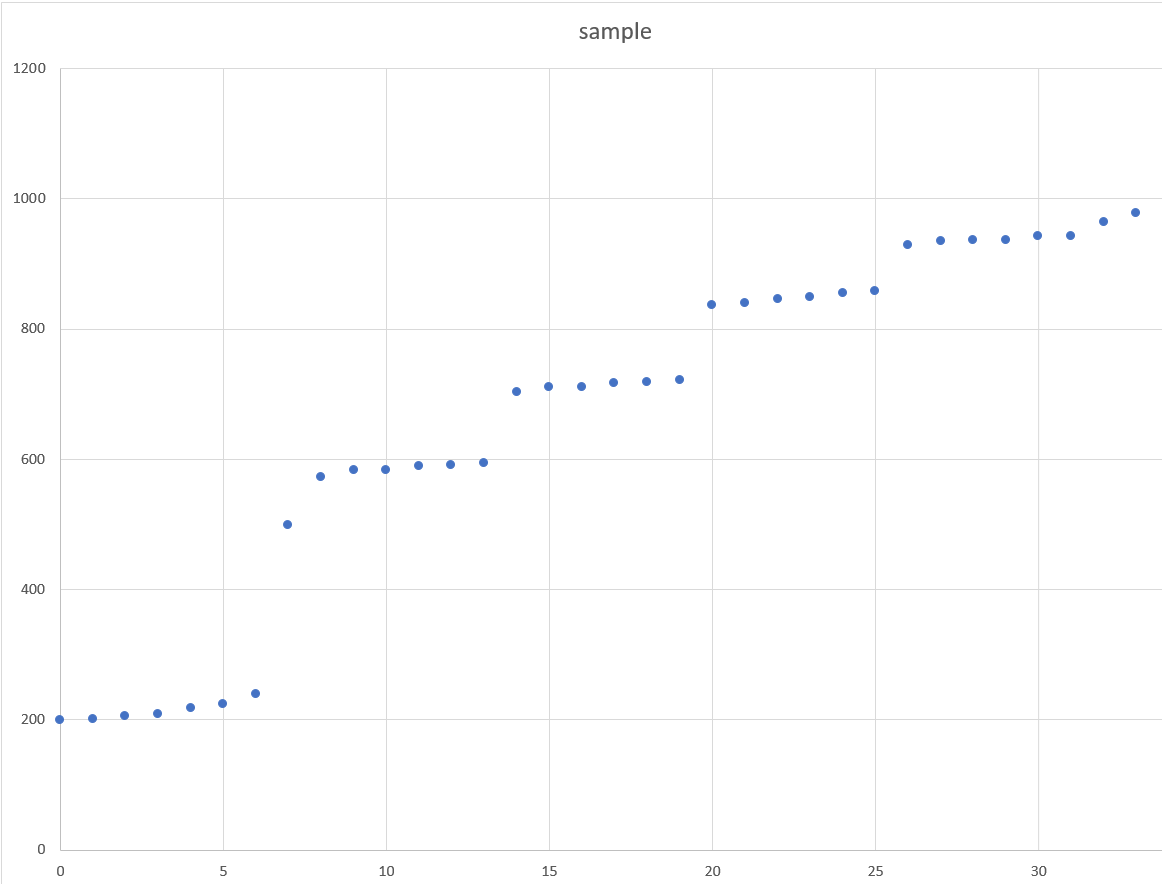Данные делятся на уровни. Количество уровней дано для меня (5 уровней в этом примере). Тем не менее, количество выборок для каждого уровня неизвестно, а также расстояния между уровнями также неизвестны. Мне нужно исключить выбросы и определить центр каждого уровня (посмотрите на вывод второго изображения. 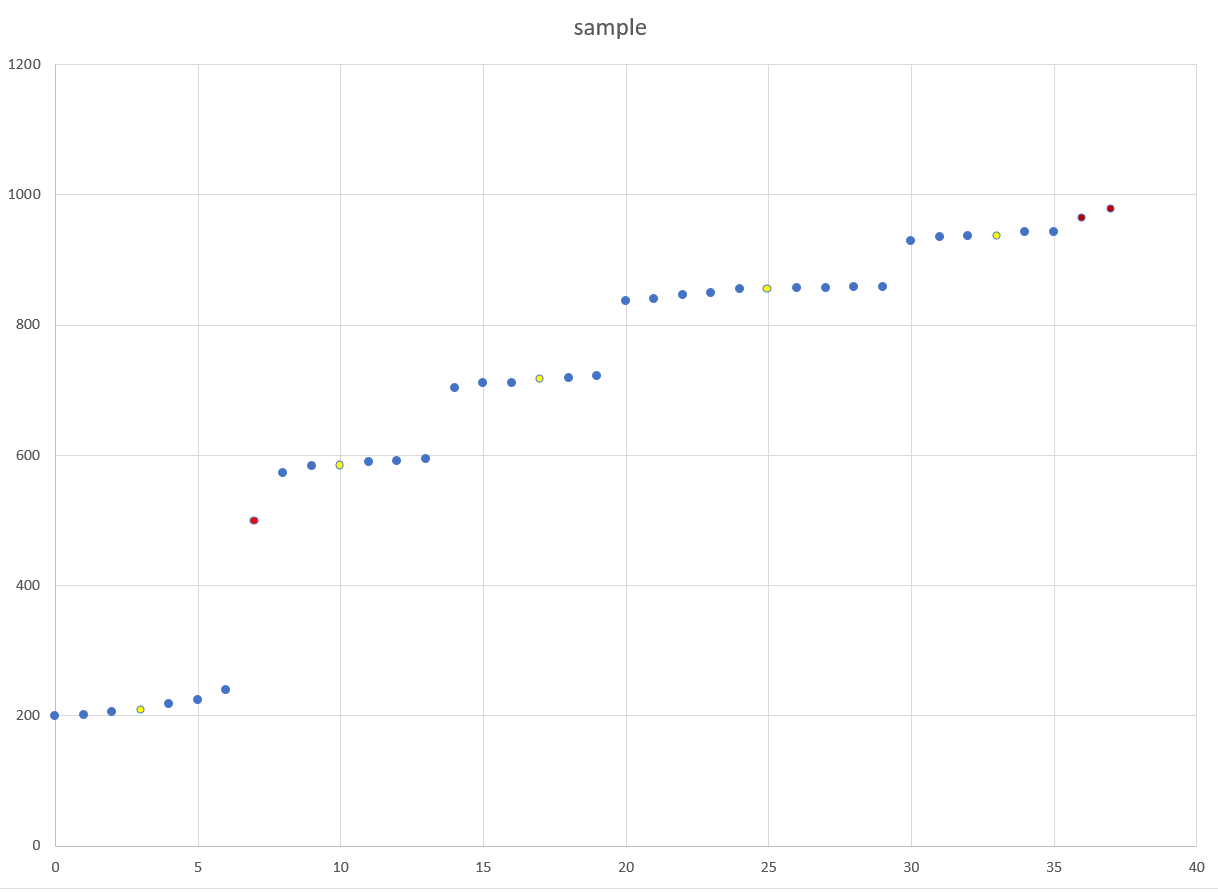Красные образцы представляют выбросы, а желтые представляют центры уровней). Есть ли какой-либо алгоритм, математическая формула, код C++ может помочь мне выполнить это требование? Я попробовал KMeans (с K = 5 в этом примере), и я получил плохой результат из-за случайных начальных K центроидов. В большинстве случаев некоторые первичные центроиды имеют один и тот же уровень, что позволяет этому уровню стать двумя кластерами, тогда как два других уровня принадлежат одному кластеру. Если я установлю начальные центроиды вручную, выбрав один центроид с каждого уровня, я получу очень хорошие результаты. Любая помощь будет оценена!

Answer 1

Если разница между двумя последовательными точками данных превышает определенное значение (рассмотрим это как Delta), то оно относится к другому кластеру.

для этого набора данных: 199 200 205 209 217 224 239 498 573 583 583 590 591 594 703 710 711 717 719 721 836 840 845 849 855 855 856 857 858 858 928 935 936 936 942 943 964 964 977 977

предположим, что дельта равна 15 (точная настройка на основе датчика), если разность последовательных точек данных не превышает 15, то они принадлежат одному кластеру. Вы можете найти центральную точку, найдя среднее значение кластера. если точка имеет близлежащую точку с разницей дельты, то это можно рассматривать как выброс. Другие варианты: мы можем варьировать дельту на основе текущего значения набора данных.

Answer 2

Это продолжение ответа @KarthikeyanMV. +1. Да, вы должны быть в состоянии определить значение для Delta. Вот процесс, который сделает это. Я пишу свой код на R, но думаю, что процесс будет понятен.

Предположительно, разрывы между группами больше, чем разрывы в любой группе, поэтому просто посмотрите на разницу между последовательными точками и спросите, где большие разрывы. Поскольку вы считаете, что должно быть 5 групп, должно быть 4 больших пробела, так что посмотрите на 4-ую самую большую разницу.

## Your data
dat = c(199, 200, 205, 209, 217, 224, 239, 498, 573, 583, 
    583, 590, 591, 594, 703, 710, 711, 717, 719, 721, 
    836, 840, 845, 849, 855, 855, 856, 857, 858, 858, 
    928, 935, 936, 936, 942, 943, 964, 977)
(Delta = sort(diff(dat), decreasing=TRUE)[4])
[1] 75

Похоже, что Delta должно быть 75, но мы не смогли учесть выбросы. Есть ли какие-либо точки, которые больше, чем Delta, как из следующего пункта выше, так и ниже? Да.

BigGaps = diff(dat) >= Delta
(Outliers = which(c(BigGaps, T) & c(T, BigGaps)))
[1] 8

Пункт 8 слишком далеко, чтобы принадлежать к группе выше или ниже. Итак, давайте удалим его и попробуем еще раз.

dat = dat[-Outliers]
(Delta = sort(diff(dat), decreasing=TRUE)[4])
[1] 70
BigGaps = diff(dat) >= Delta
(Outliers = which(c(BigGaps, T) & c(T, BigGaps)))
integer(0)

После того, как мы удалим точку 8, новая дельта равна 70. Мы проверяем выбросы, используя новую дельту (70), и не находим ничего. Итак, давайте кластеризуем, используя Delta = 70.

Cluster = cumsum(c(1, diff(dat)>=Delta))
plot(dat, pch=20, col=Cluster+1)

В основном это были кластеры, которые вам нужны, за исключением того, что они включали последние две точки в самом высоком кластере, а не объявляли их выбросами. Я не понимаю, почему они должны быть выбросами, а не частью этой группы. Может быть, вы могли бы уточнить, почему вы думаете, что они не должны быть включены.

Я надеюсь, что это помогает.

Answer 3

Я заметил, что эти уровни выглядят как линии. Вы могли бы сделать что-то подобное:

1. sort the points
2. take the first two unprocessed points into an ordered set called the current line
3. lay a line between the first and last point of the set
4. test whether the line formed by the first point and the next unprocessed point
    form a line that has an angle lower than some threshold to the other line
5. If yes, add the point and go to 3
6. If no, store the current line somewhere and start again at 2

Вы также можете начать с проверки, имеют ли первые две точки такой линии угол к оси x, который находится выше другого порога, и, если это так, сохранить первую точку как нечто особенное. Выбросы.

Другой вариант будет идти только по углу соединения двух точек с осью X. При изменении уровня будет гораздо больший угол (наклон, уклон), чем между двумя точками на уровне.

Answer 4

Я бы предложил DBSCAN вместо K-Means.

Это алгоритм кластеризации на основе плотности, который группирует точки данных, которые находятся в той же близости друг к другу, без необходимости определять начальные k или центроиды, такие как K-средние.

В DBSCAN расстояние и k-соседи определяются пользователем. Если вы знаете, что индекс имеет постоянный интервал, DBSCAN может подойти для решения вашей проблемы.