Python/matplotlib: построение трехмерного куба, сферы и вектора?
Я ищу, как построить что-то с меньшим количеством инструкций, насколько это возможно, с помощью matplotlib, но я не нахожу никакой помощи в документации.
Я хочу построить следующие вещи:
- каркасный куб с центром в 0 с длиной стороны 2
- сфера "каркас" с центром в 0 с радиусом 1
- точка в координатах [0, 0, 0]
- вектор, который начинается в этой точке и идет к [1, 1, 1]
Как это сделать?
2 ответа
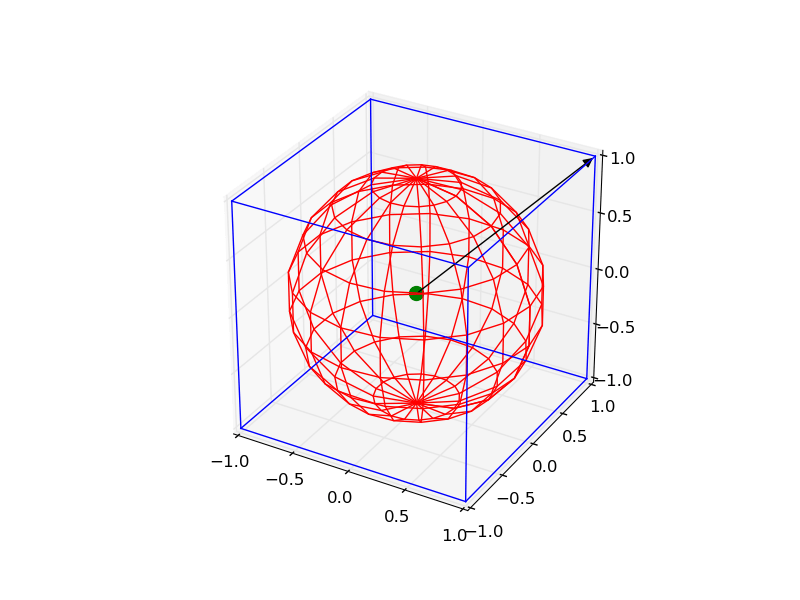
Это немного сложно, но вы можете нарисовать все объекты с помощью следующего кода:
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
from itertools import product, combinations
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.set_aspect("equal")
# draw cube
r = [-1, 1]
for s, e in combinations(np.array(list(product(r, r, r))), 2):
if np.sum(np.abs(s-e)) == r[1]-r[0]:
ax.plot3D(*zip(s, e), color="b")
# draw sphere
u, v = np.mgrid[0:2*np.pi:20j, 0:np.pi:10j]
x = np.cos(u)*np.sin(v)
y = np.sin(u)*np.sin(v)
z = np.cos(v)
ax.plot_wireframe(x, y, z, color="r")
# draw a point
ax.scatter([0], [0], [0], color="g", s=100)
# draw a vector
from matplotlib.patches import FancyArrowPatch
from mpl_toolkits.mplot3d import proj3d
class Arrow3D(FancyArrowPatch):
def __init__(self, xs, ys, zs, *args, **kwargs):
FancyArrowPatch.__init__(self, (0, 0), (0, 0), *args, **kwargs)
self._verts3d = xs, ys, zs
def draw(self, renderer):
xs3d, ys3d, zs3d = self._verts3d
xs, ys, zs = proj3d.proj_transform(xs3d, ys3d, zs3d, renderer.M)
self.set_positions((xs[0], ys[0]), (xs[1], ys[1]))
FancyArrowPatch.draw(self, renderer)
a = Arrow3D([0, 1], [0, 1], [0, 1], mutation_scale=20,
lw=1, arrowstyle="-|>", color="k")
ax.add_artist(a)
plt.show()
Для рисования только стрелки есть более простой способ:
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
fig = plt.figure()
ax = fig.gca(projection='3d')
ax.set_aspect("equal")
#draw the arrow
ax.quiver(0,0,0,1,1,1,length=1.0)
plt.show()
Quiver действительно может быть использован для построения нескольких векторов за один раз. Использование выглядит следующим образом:- [от http://matplotlib.org/mpl_toolkits/mplot3d/tutorial.html?highlight=quiver
колчан (X, Y, Z, U, V, W, ** Kwargs)
Аргументы:
X, Y, Z: координаты x, y и z расположения стрелок
U, V, W: x, y и z компоненты стрелочных векторов
Аргументы могут быть массивными или скалярными.
Ключевые аргументы:
длина: [1.0 | float] Длина каждого колчана, по умолчанию 1.0, единица с осями
arrow_length_ratio: [0.3 | float] Соотношение наконечника стрелы к колчану, по умолчанию 0,3
пивот: ['tail' | "средний" | 'tip'] Часть стрелки, которая находится в точке сетки; стрелка вращается вокруг этой точки, отсюда и название оси вращения. По умолчанию это "хвост"
нормализовать: [Ложь | True] Когда True, все стрелки будут одинаковой длины. По умолчанию это значение False, где стрелки будут разной длины в зависимости от значений u, v, w.
Мой ответ - объединение двух вышеупомянутых с расширением области рисования с пользовательской непрозрачностью и некоторыми аннотациями. Он находит применение в визуализации b-вектора на сфере для магнитно-резонансного изображения (МРТ). Надеюсь, что вы найдете ее полезной:
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
import numpy as np
fig = plt.figure()
ax = fig.gca(projection='3d')
# draw sphere
u, v = np.mgrid[0:2*np.pi:50j, 0:np.pi:50j]
x = np.cos(u)*np.sin(v)
y = np.sin(u)*np.sin(v)
z = np.cos(v)
# alpha controls opacity
ax.plot_surface(x, y, z, color="g", alpha=0.3)
# a random array of 3D coordinates in [-1,1]
bvecs= np.random.randn(20,3)
# tails of the arrows
tails= np.zeros(len(bvecs))
# heads of the arrows with adjusted arrow head length
ax.quiver(tails,tails,tails,bvecs[:,0], bvecs[:,1], bvecs[:,2],
length=1.0, normalize=True, color='r', arrow_length_ratio=0.15)
ax.set_xlabel('X-axis')
ax.set_ylabel('Y-axis')
ax.set_zlabel('Z-axis')
ax.set_title('b-vectors on unit sphere')
plt.show()