Python: построение равномерно распределенных сфер в Matplotlib

Question

Я пытаюсь создать сюжет примерно так:

Там, где есть сферы выше всех минимумов.

Поверхность может быть аппроксимирована графиком sin(x)*sin(y):

import numpy as np
import matplotlib.pyplot as plt

def func(x, y):
  return np.sin(2*np.pi*x)*np.sin(2*np.pi*y) / 3

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
x = y = np.arange(-1.0, 1.0, 0.05)
X, Y = np.meshgrid(x, y)
zs = np.array([func(x,y) for x,y in zip(np.ravel(X), np.ravel(Y))])
Z = zs.reshape(X.shape)

ax.plot_surface(X, Y, Z, color="grey")
ax.set_zlim3d(-1,1)

plt.show()

Однако я не уверен, как добавить в это равномерно распределенные сферы. Кто-нибудь сможет помочь?

Answer 1

Используя matplotlib, вы неизбежно столкнетесь с проблемами скрытия объектов за другими. Об этом также говорится в FAQ по matplotlib 3d, и рекомендуется использовать Mayavi.

В Mayavi решение будет выглядеть так:

from mayavi import mlab
import numpy as np

### SURFACE '''
x,y = np.meshgrid(np.linspace(-2.5,2), np.linspace(-2,2))
f = lambda x,y: .4*np.sin(2*np.pi*x)*np.sin(2*np.pi*y)
z=f(x,y)
mlab.surf(x.T,y.T,z.T, colormap="copper")

### SPHERES '''
px,py = np.meshgrid(np.arange(-2,2)+.25, np.arange(-2,2)+.75)
px,py = px.flatten(),py.flatten()
pz = np.ones_like(px)*0.05
r = np.ones_like(px)*.4
mlab.points3d(px,py,pz,r, color=(0.9,0.05,.3), scale_factor=1)


mlab.show()

Answer 2

Вам нужно определить минимумы функции, которые (с вашей параметризацией) равны (x = целое число + 0,25, y= целое число + 0,75) или наоборот. Затем вы можете просто параметризовать сферы, используя сферические координаты (например, как здесь сделано: python matplotlib: рисование трехмерной сферы с окружностями) и построить сферы.

Теперь приходят хорошие и плохие новости:

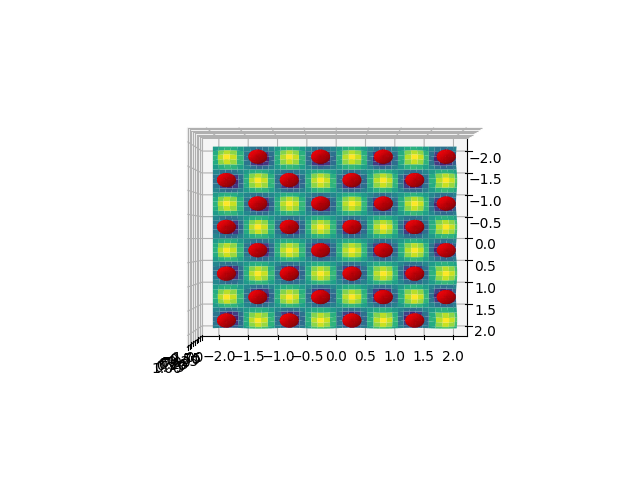
1.) Хорошая новость заключается в том, что минимумы правильно определены и сферы созданы. На графике ниже вы можете видеть, что они находятся прямо над синими частями графика поверхности (где синие части показывают минимумы).

2.) Плохая новость заключается в том, что вам будет трудно искать другой угол, где сферы на самом деле правильно отображаются. Я не знаю решения этого довольно раздражающего поведения, поэтому вам, вероятно, придется поиграть, пока вы не найдете правильный угол. Повеселись!

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

def func(x, y):
  return np.sin(2*np.pi*x)*np.sin(2*np.pi*y) / 3

fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
x = y = np.arange(-2.0, 2.0, 0.05)

# Get the minima of the function.
minsx1 = np.arange(int(np.amin(x)) + 0.25, int(np.amax(x)) + 0.25 + 1, 1)
minsy1 = np.arange(int(np.amin(y)) + 0.75, int(np.amax(y)) + 0.75 + 1, 1)
minsx2 = np.arange(int(np.amin(x)) + 0.75, int(np.amax(x)) + 0.75 + 1, 1)
minsy2 = np.arange(int(np.amin(y)) + 0.25, int(np.amax(y)) + 0.25 + 1, 1)

X, Y = np.meshgrid(x, y)
zs = np.array([func(x,y) for x,y in zip(np.ravel(X), np.ravel(Y))])
Z = zs.reshape(X.shape)

# Color map for better detection of minima (blue)
ax.plot_surface(X, Y, Z, cmap="viridis")
ax.set_zlim3d(-1,1)

# Spherical coordinates
r = 0.15
phi = np.linspace(0, 2 * np.pi, 30)
theta = np.linspace(0, np.pi, 30)

# Write spherical coordinates in cartesian coordinates.
x = r * np.outer(np.cos(phi), np.sin(theta))
y = r * np.outer(np.sin(phi), np.sin(theta))
z = r * np.outer(np.ones(np.size(phi)), np.cos(theta))

# Plot the spheres.
for xp in minsx1:
    for yp in minsy1:
        sphere = ax.plot_surface(x+xp, y+yp, z+0.35, color='r')
for xp in minsx2:
    for yp in minsy2:
        sphere = ax.plot_surface(x+xp, y+yp, z+0.35, color='r')
ax.view_init(elev=90, azim=0)
plt.savefig('test.png')
plt.show()