python matplotlib: рисование трехмерной сферы с окружностями

Question

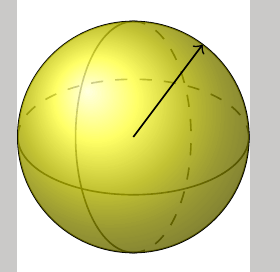
Я пытаюсь нарисовать сферу, подобную этой, используя matplotlib:

но я не могу найти способ иметь пунктирные линии на спине, а вертикальная окружность выглядит немного странно

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

fig = plt.figure(figsize=(12,12), dpi=300)
ax = fig.add_subplot(111, projection='3d')
ax.set_aspect('equal')

u = np.linspace(0, 2 * np.pi, 100)
v = np.linspace(0, np.pi, 100)

x = 1 * np.outer(np.cos(u), np.sin(v))
y = 1 * np.outer(np.sin(u), np.sin(v))
z = 1 * np.outer(np.ones(np.size(u)), np.cos(v))
#for i in range(2):
#    ax.plot_surface(x+random.randint(-5,5), y+random.randint(-5,5), z+random.randint(-5,5),  rstride=4, cstride=4, color='b', linewidth=0, alpha=0.5)

ax.plot_surface(x, y, z,  rstride=4, cstride=4, color='b', linewidth=0, alpha=0.5)
ax.plot(np.sin(theta),np.cos(u),0,color='k')
ax.plot([0]*100,np.sin(theta),np.cos(u),color='k')

Answer 1

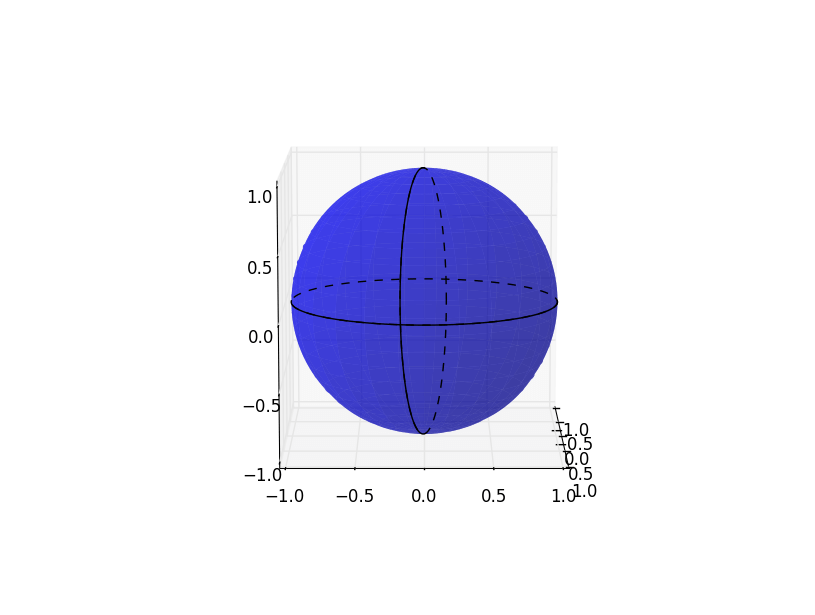
В примере, который вы показываете, я не думаю, что круги могут быть перпендикулярны друг другу (то есть один является экватором, а другой проходит через северный полюс и южный полюс). Если горизонтальный круг является экватором, то северный полюс должен находиться где-то на вертикальной линии, проведенной через центр желтого круга, представляющего сферу. В противном случае правая сторона экватора будет выглядеть выше или ниже, чем левая. Однако эллипс, представляющий полярный круг, пересекает только эту центральную линию сверху и снизу желтого круга. Поэтому северный полюс находится наверху сферы, что означает, что мы должны смотреть прямо на экваторе, что означает, что он должен выглядеть как линия, а не как эллипс.

Вот код для воспроизведения чего-то похожего на рисунок, который вы разместили:

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.set_aspect('equal')

u = np.linspace(0, 2 * np.pi, 100)
v = np.linspace(0, np.pi, 100)

x = 1 * np.outer(np.cos(u), np.sin(v))
y = 1 * np.outer(np.sin(u), np.sin(v))
z = 1 * np.outer(np.ones(np.size(u)), np.cos(v))
#for i in range(2):
#    ax.plot_surface(x+random.randint(-5,5), y+random.randint(-5,5), z+random.randint(-5,5),  rstride=4, cstride=4, color='b', linewidth=0, alpha=0.5)
elev = 10.0
rot = 80.0 / 180 * np.pi
ax.plot_surface(x, y, z,  rstride=4, cstride=4, color='b', linewidth=0, alpha=0.5)
#calculate vectors for "vertical" circle
a = np.array([-np.sin(elev / 180 * np.pi), 0, np.cos(elev / 180 * np.pi)])
b = np.array([0, 1, 0])
b = b * np.cos(rot) + np.cross(a, b) * np.sin(rot) + a * np.dot(a, b) * (1 - np.cos(rot))
ax.plot(np.sin(u),np.cos(u),0,color='k', linestyle = 'dashed')
horiz_front = np.linspace(0, np.pi, 100)
ax.plot(np.sin(horiz_front),np.cos(horiz_front),0,color='k')
vert_front = np.linspace(np.pi / 2, 3 * np.pi / 2, 100)
ax.plot(a[0] * np.sin(u) + b[0] * np.cos(u), b[1] * np.cos(u), a[2] * np.sin(u) + b[2] * np.cos(u),color='k', linestyle = 'dashed')
ax.plot(a[0] * np.sin(vert_front) + b[0] * np.cos(vert_front), b[1] * np.cos(vert_front), a[2] * np.sin(vert_front) + b[2] * np.cos(vert_front),color='k')

ax.view_init(elev = elev, azim = 0)


plt.show()

Answer 2

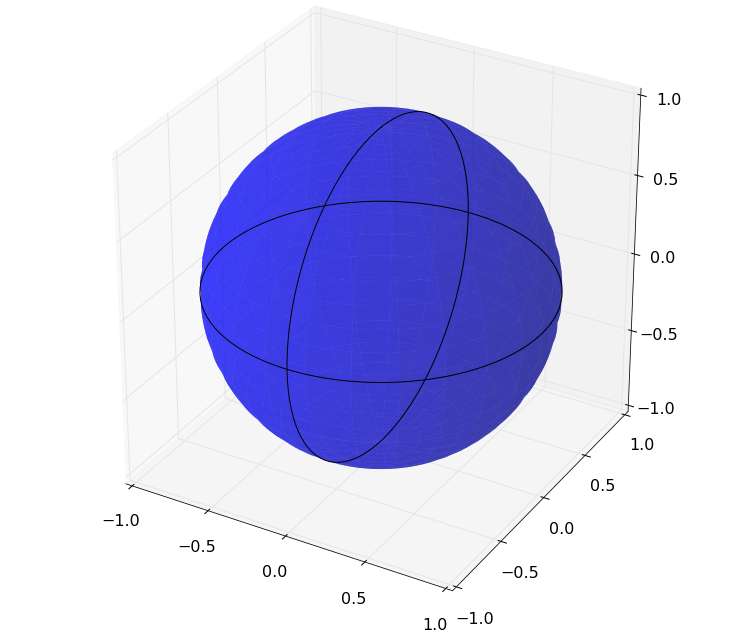
Я пытаюсь сделать что-то подобное, но если вы установите альфа на 1, то линии исчезнут за поверхностным графиком.