Как генерировать случайные числа с предопределенным распределением вероятностей?

Я хотел бы реализовать функцию в Python (используя numpy), который принимает математическую функцию (например, p(x) = e^(-x) как показано ниже) в качестве входных данных и генерирует случайные числа, которые распределяются в соответствии с вероятностным распределением этой математической функции. И мне нужно построить их так, чтобы мы могли увидеть распределение.

На самом деле мне нужна точно функция генератора случайных чисел для следующих двух математических функций в качестве входных данных, но если она может принимать другие функции, почему бы и нет:

1) p(x) = e^(-x)
2) g(x) = (1/sqrt(2*pi)) * e^(-(x^2)/2)

Кто-нибудь есть идеи, как это выполнимо в Python?

Источник

2 ответа

Решение

Для простых дистрибутивов, таких как те, которые вам нужны, или если у вас есть возможность легко инвертировать CDF в закрытой форме, вы можете найти множество сэмплеров в NumPy, как правильно указано в ответе Оливье.

Для произвольных распределений вы можете использовать методы выборки Маркова-Цепи Монте-Карло.

Самым простым и, возможно, более простым для понимания вариантом этих алгоритмов является выборка Метрополис.

Основная идея выглядит так:

  • начать со случайной точки x и сделать случайный шаг xnew = x + delta
  • оценить желаемое распределение вероятностей в начальной точке p(x) и в новом p(xnew)
  • если новая точка более вероятна p(xnew)/p(x) >= 1 принять движение
  • если новая точка менее вероятна, случайным образом решите, принимать ее или отклонять, в зависимости от того, насколько вероятна 1 новая точка
  • Новый шаг с этой точки и повторить цикл

Можно показать, см., Например, Сокал 2, что точки, отобранные этим методом, следуют распределению вероятности принятия.

Обширная реализация методов Монте-Карло в Python может быть найдена в PyMC3 пакет.

Пример реализации

Вот игрушечный пример, чтобы показать вам основную идею, никоим образом не подразумеваемую в качестве эталонной реализации. Пожалуйста, обратитесь к зрелым пакетам для любой серьезной работы.

def uniform_proposal(x, delta=2.0):
    return np.random.uniform(x - delta, x + delta)

def metropolis_sampler(p, nsamples, proposal=uniform_proposal):
    x = 1 # start somewhere

    for i in range(nsamples):
        trial = proposal(x) # random neighbour from the proposal distribution
        acceptance = p(trial)/p(x)

        # accept the move conditionally
        if np.random.uniform() < acceptance:
            x = trial

        yield x

Давайте посмотрим, работает ли он с некоторыми простыми дистрибутивами

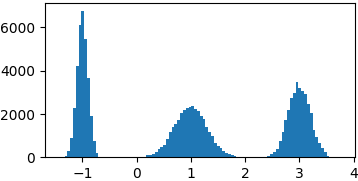
Гауссова смесь 

def gaussian(x, mu, sigma):
    return 1./sigma/np.sqrt(2*np.pi)*np.exp(-((x-mu)**2)/2./sigma/sigma)

p = lambda x: gaussian(x, 1, 0.3) + gaussian(x, -1, 0.1) + gaussian(x, 3, 0.2)
samples = list(metropolis_sampler(p, 100000))

мегаполис гауссиан сумма

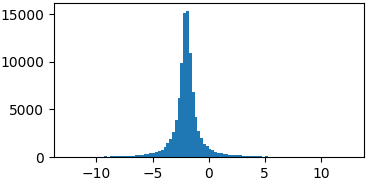
коши 

def cauchy(x, mu, gamma):
    return 1./(np.pi*gamma*(1.+((x-mu)/gamma)**2))

p = lambda x: cauchy(x, -2, 0.5)
samples = list(metropolis_sampler(p, 100000))

мегаполис коши

Произвольные функции

Вам не обязательно выбирать из правильных распределений вероятностей. Возможно, вам просто придется ввести ограниченный домен, в котором вы можете выбрать случайные шаги 3

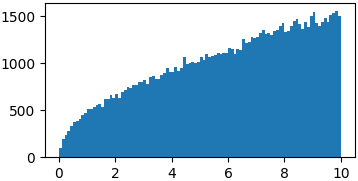
p = lambda x: np.sqrt(x)
samples = list(metropolis_sampler(p, 100000, domain=(0, 10)))

мегаполис sqrt

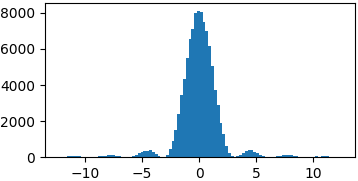
p = lambda x: (np.sin(x)/x)**2
samples = list(metropolis_sampler(p, 100000, domain=(-4*np.pi, 4*np.pi)))

мегаполис синк

Выводы

Еще слишком много, чтобы сказать, о распределении предложений, конвергенции, корреляции, эффективности, приложениях, байесовском формализме, других сэмплерах MCMC и т. Д. Я не думаю, что это правильное место, и есть много гораздо лучшего материала, чем то, что Я мог бы написать здесь доступны онлайн.

  1. Идея здесь состоит в том, чтобы способствовать разведке, где вероятность выше, но все же смотреть на регионы с низкой вероятностью, поскольку они могут привести к другим пикам. Основополагающим является выбор распределения предложения, то есть то, как вы выбираете новые точки для изучения. Слишком маленькие шаги могут ограничить вас в ограниченной области вашего распространения, слишком большие могут привести к очень неэффективному исследованию.

  2. Физика ориентирована. Байесовский формализм (Метрополис-Гастингс) предпочтителен в наши дни, но ИМХО его немного сложнее понять новичкам. В Интернете доступно множество учебных пособий, например, из Университета Дьюка.

  3. Реализация, показанная не для того, чтобы не добавлять слишком много путаницы, но это просто, вам просто нужно обернуть пробные шаги на краях домена или заставить желаемую функцию обнуляться вне домена.

Источник

NumPy предлагает широкий спектр распределений вероятностей.

Первая функция - экспоненциальное распределение с параметром 1.

np.random.exponential(1)

Второе - нормальное распределение со средним 0 и дисперсией 1.

np.random.normal(0, 1)

Обратите внимание, что в обоих случаях аргументы являются необязательными, поскольку они являются значениями по умолчанию для этих распределений.

В качестве заметки вы также можете найти эти дистрибутивы в random модуль как random.expovariate а также random.gauss соответственно.

Более общие распределения

Хотя NumPy, вероятно, удовлетворит все ваши потребности, помните, что вы всегда можете вычислить обратную интегральную функцию распределения вашего распределения и входные значения из равномерного распределения.

inverse_cdf(np.random.uniform())

Например, если NumPy не предоставляет экспоненциальное распределение, вы можете сделать это.

exponential = lambda: -np.log(-np.random.uniform())

Если вы сталкиваетесь с дистрибутивами, которые CDF нелегко вычислить, подумайте над отличным ответом filippo.

Источник
Другие вопросы по тегам