Оценка позы: определить правильность вращения и матрицы преобразования

Question

В последнее время я борюсь с проблемой оценки позы с одной камерой. У меня есть несколько 3D-точек и соответствующих 2D-точек на изображении. Затем я использую solvePnP, чтобы получить векторы вращения и перемещения. Проблема в том, как я могу определить, являются ли векторы правильными результатами?

Теперь я использую косвенный способ сделать это:
Я использую матрицу вращения, вектор перевода и трехмерные координаты мира определенной точки, чтобы получить координаты этой точки в системе камер. Тогда все, что мне нужно сделать, это определить, являются ли координаты разумными. Я думаю, что знаю направления осей x, y и z системы камеры.

• Является ли Camera Center источником системы Camera?
• Теперь рассмотрим x компонент этой точки. Эквивалентен ли x расстоянию камеры и точке в мировом пространстве в направлении оси X камеры (знак может быть затем определен по точке, расположенной на какой стороне камеры)?

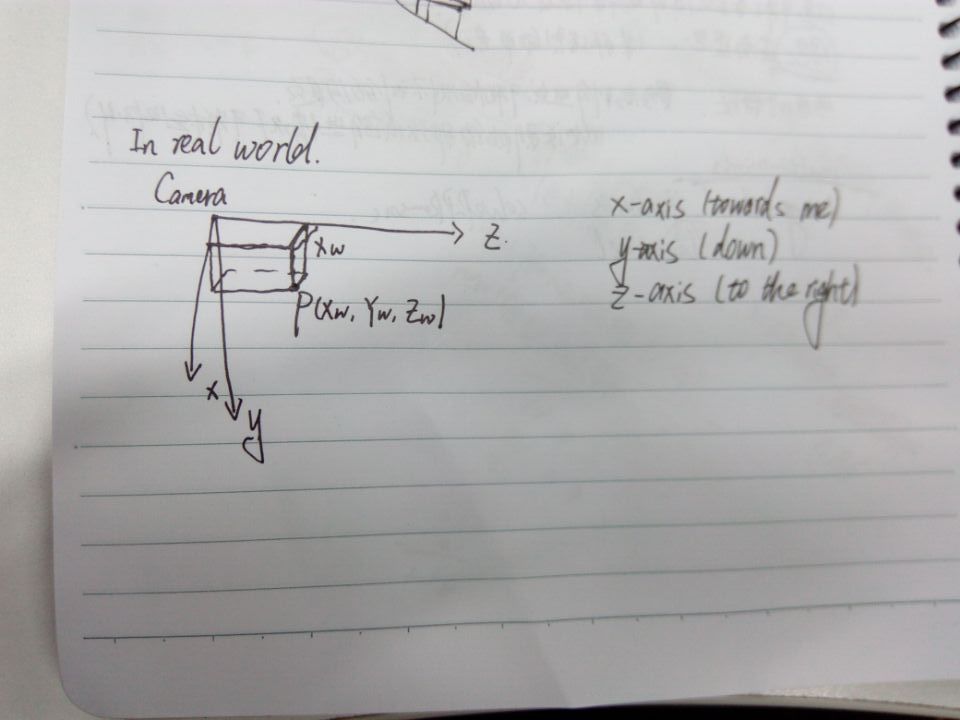
На рисунке внизу показано мировое пространство, а изображенные оси - в системе камер.

========How Camera and the point be placed in the world space=============
   |
   |              
Camera--------------------------> Z axis
   |                |} Xw?
   |                P(Xw, Yw, Zw)
   |              
   v x-axis     

Мои результаты rvec и tvec кажутся правильными и неправильными. Для указанной точки значение z кажется разумным, я имею в виду, что если эта точка находится на расстоянии около одного метра от камеры в направлении z, то значение z составляет около 1. Но для x и y, в соответствии с расположением Я думаю, что x и y должны быть положительными, но они отрицательны. Более того, шаблон, обнаруженный на исходном изображении, выглядит следующим образом:

Но используя координаты точек, рассчитанные в системе камеры, и внутренние параметры камеры, я получаю изображение, подобное этому:

Цель держит свой образец. Но он двигался снизу справа вверху слева. Я не могу понять почему.

Answer 1

Теперь я знаю ответы.

• Да, центр камеры является источником системы координат камеры.

• Учтите, что координаты в системе камер рассчитываются как (xc,yc,zc). Тогда xc должно быть расстоянием между камерой и точкой в ​​реальном мире в направлении x.

Далее, как определить, правильны ли выходные матрицы?
1. как указывает @eidelen, ошибка обратного проецирования является одним из ориентировочных показателей.
2. Рассчитать координаты точек по их координатам в мировой системе координат и матрицах.

Так почему же я получил неправильный результат (рисунок остался, но переместился в другую область изображения)?
параметр cameraMatrix в solvePnP() представляет собой матрицу, предоставляющую параметры внешних параметров камеры. В матрице камеры вы должны использовать ширину /2 и высоту /2 для cx и cy. Пока я использую ширину и высоту изображения размером. Я думаю, что это вызвало ошибку. После того, как я исправил это и повторно калибровал камеру, все кажется хорошо.

Answer 2

Да, центр камеры является источником системы координат камеры, которая, кажется, следует за этим сообщением.

В случае оценки позы камеры, значение кажется разумным и может быть названо ошибкой обратного проецирования. Это мера того, насколько хорошо ваши результирующие вращение и перемещение отображают 3D-точки на 2D-пиксели. К сожалению, solvePnP не возвращает меру остаточной ошибки. Поэтому нужно вычислить это:

cv::solvePnP(worldPoints, pixelPoints, camIntrinsics, camDistortion, rVec, tVec);

// Use computed solution to project 3D pattern to image
cv::Mat projectedPattern;
cv::projectPoints(worldPoints, rVec, tVec, camIntrinsics, camDistortion, projectedPattern);

// Compute error of each 2D-3D correspondence.
std::vector<float> errors;
for( int i=0; i < corners.size(); ++i)
{
    float dx = pixelPoints.at(i).x - projectedPattern.at<float>(i, 0);
    float dy = pixelPoints.at(i).y - projectedPattern.at<float>(i, 1);
    // Euclidean distance between projected and real measured pixel
    float err = sqrt(dx*dx + dy*dy); 

    errors.push_back(err);
}

// Here, compute max or average of your "errors"

Средняя ошибка обратной проекции откалиброванной камеры может быть в диапазоне 0 - 2 пикселя. Согласно вашим двум фотографиям, это было бы намного больше. Для меня это похоже на проблему масштабирования. Если я прав, вы сами рассчитываете проекцию. Может быть, вы можете попробовать один раз cv::projectPoints() и сравнить.

Когда дело доходит до преобразований, я научился не следовать своему воображению:) Первое, что я делаю с возвращенными rVec и tVec, обычно создает из них матрицу жесткого преобразования 4x4 (я однажды разместил здесь код). Это делает вещи еще менее интуитивно понятными, но вместо этого он компактен и удобен.