Вращение группы векторов

Question

Я пытаюсь повернуть группу векторов, отобранных для нормали треугольника

Если бы это было правильно, случайно выбранная полусфера выровнялась бы с треугольником.

В настоящее время я генерирую его на оси Z и пытаюсь повернуть все сэмплы к нормали треугольника.

но вроде бы "просто выключено"

glm::quat getQuat(glm::vec3 v1, glm::vec3 v2)
{

    glm::quat myQuat;
    float dot = glm::dot(v1, v2);
    if (dot != 1)
    {
        glm::vec3 aa = glm::normalize(glm::cross(v1, v2));
        float w = sqrt(glm::length(v1)*glm::length(v1) * glm::length(v2)*glm::length(v2)) + dot;
        myQuat.x = aa.x;
        myQuat.y = aa.y;
        myQuat.z = aa.z;
        myQuat.w = w;
    }
    return myQuat;
}

Который я вытащил из нижней части этой страницы: http://lolengine.net/blog/2013/09/18/beautiful-maths-quaternion-from-vectors

Затем я:

glm::vec3 zaxis = glm::normalize( glm::vec3(0, 0, 1) );  // hardcoded but test orginal axis
glm::vec3 n1 = glm::normalize( glm::cross((p2 - p1), (p3 - p1)) ); //normal
glm::quat myQuat = glm::normalize(getQuat(zaxis, n1));

glm::mat4 rotmat = glm::toMat4(myQuat); //make a rotation matrix
glm::vec4 n3 = rotmat * glm::vec4(n2,1); // current vector I am trying to rotate

Answer 1

Построить матрицу преобразования 4х4 вместо кватернионов.

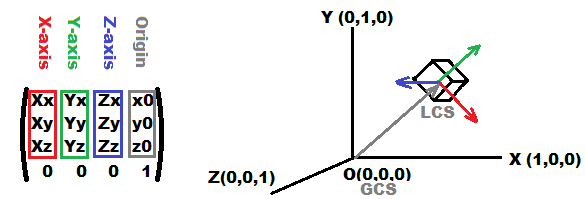
1. Не забывайте, что OpenGL имеет столбцовую матрицу

   Таким образом, для double m[16];
   является X вектор оси в m[ 0],m[ 1],m[ 2]
   является Y вектор оси в m[ 4],m[ 5],m[ 6]
   является Z вектор оси в m[ 8],m[ 9],m[10]
   и положение в m[12],m[13],m[14]

   LCS означает локальную систему координат (ваш треугольник или объект или что-то еще)
   и GCS означает глобальную систему координат (мир или что-то еще).

   Все X,Y,Z векторы должны быть нормализованы к единичным векторам, иначе произойдет масштабирование.

2. строительство

   1. задавать Z-оси вектор к вашему треугольнику нормальный
   2. установить положение (начало координатLCS) в средней точке вашего треугольника (или средней точке из его вершин)

   3. теперь вам просто нужно X а также Y Оси, которые легко

      позволять X = any triangle vertex - triangle midpoint
      или же X = substraction of any 2 vertexes of triangle

      Единственное условие, которое должно быть выполнено для X является то, что он должен лежать на плоскости треугольника.
      Теперь позвольте Y = X x Z перекрестный продукт создаст вектор перпендикулярно X а также Z (который также лежит в плоскости треугольника).

   4. Теперь поместите все это в матрицу и загрузите его в OpenGL как ModelView матрица или что-нибудь еще.