Стандартная сетка для вогнутых шестиугольников с двумя ртами?

Question

Стандартная сетка для вогнутых шестиугольников с двумя ртами?

Я планирую визуализацию потоков через вогнутые бисимметричные шестиугольники с двумя горловинами.

Пример, где длина стороны d1 равна другой длине стороны d2:

введите описание изображения здесь

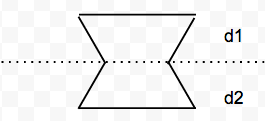
какое наименование я изначально обсуждал здесь о неправильных шестиугольниках.

Существует стандартный инструмент Mesh, где вы можете рисовать свои собственные сетки, но я хотел бы иметь некоторую стандартную библиотеку, чтобы я мог лучше взаимодействовать с другими при моделировании потока позже. Я не нашел никакой библиотеки Mesh для шестиугольников в MathCentral File Exchange здесь.

Есть ли стандартная библиотека Mesh для неправильных шестиугольников? Я открыт для любых других языков, потому что я мог читать код и преобразовывать его в библиотеку Matlab.

9

geometry mesh convex-optimization finite-element-analysis non-convex

Источник

user54964 23 май '15 в 09:57

5 ответов

Решение

Например, вы можете взглянуть на пример, сделанный Александрой Баумгарт и Хазуки Окуда с использованием Mathematica. Это реализовано с помощью Manipulate, эффективно создающего базовый интерфейс.

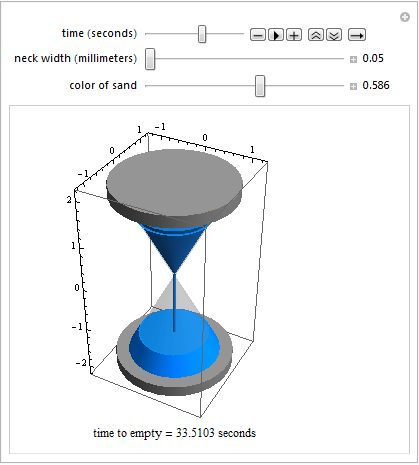
Код:

Manipulate[
Grid[{{Show[
ParametricPlot3D[{1.25Cos[t], 1.25 Sin[t],s+2-2w},{s,0,.25},{t,0,2Pi},PlotStyle->Directive[Opacity[1],Gray],Mesh->None, Lighting->"Neutral"], 
ParametricPlot3D[{r Cos[t], r Sin[t],2.25-2w},{r,0,1.25},{t,0,2Pi},PlotStyle->Directive[Opacity[1],Gray],Mesh->None, Lighting->"Neutral"],
ParametricPlot3D[{r Cos[t], r Sin[t],2-2w},{r,0,1.25},{t,0,2Pi},PlotStyle->Directive[Opacity[1],Gray],Mesh->None, Lighting->"Neutral"],
ParametricPlot3D[{1.25Cos[t], 1.25 Sin[t],s-2.25+2w},{s,0,.25},{t,0,2Pi},PlotStyle->Directive[Opacity[1],Gray],Mesh->None, Lighting->"Neutral"],
ParametricPlot3D[{r Cos[t], r Sin[t],-2.25+2w},{r,0,1.25},{t,0,2Pi},PlotStyle->Directive[Opacity[1],Gray],Mesh->None],
ParametricPlot3D[{r Cos[t], r Sin[t],-2+2w},{r,0,1.25},{t,0,2Pi},PlotStyle->Directive[Opacity[1],Gray],Mesh->None, Lighting->"Neutral"],  
ParametricPlot3D[{(1-s/2) Cos[t],(1-s/2) Sin[t],Max[0,-s+2 ]},{s,Min[2-(2^(2/3) (2 \[Pi]-Min[2Pi,3 V((w^2)/(.04))])^(1/3))/\[Pi]^(1/3)-w,1.99],2},{t,0, 2 Pi},PlotStyle->Directive[Opacity[1],Hue[a]],Mesh->None, Lighting->"Neutral"],
ParametricPlot3D[{r Cos[t], r Sin[t],Max[0,(2^(2/3) (2 \[Pi]-Min[2Pi,3 V((w^2)/(.04))])^(1/3))/\[Pi]^(1/3)-w]},{r,0, .000000000001+w+((2^(2/3) (2 \[Pi]-Min[2Pi,3 V((w^2)/(.04))])^(1/3))/\[Pi]^(1/3)-w)/2},{t,0,2Pi},PlotStyle->Directive[Opacity[1], Hue[a]],Mesh->None, Lighting->"Neutral"],
ParametricPlot3D[{r Cos[t], r Sin[t], Min[0,-(2^(2/3) (2 \[Pi]-Min[2Pi,3 V((w^2)/(.04))])^(1/3))/\[Pi]^(1/3)]},{r, 0, .00000000001+w+((2^(2/3) (2 \[Pi]-Min[2Pi,3 V((w^2)/(.04))])^(1/3))/\[Pi]^(1/3)-w)/2},{t,0,2Pi},PlotStyle->Directive[Opacity[1],Hue[a]],Mesh->None, Lighting->"Neutral"],
ParametricPlot3D[{(1-s/2) Cos[t],(1-s/2) Sin[t],Min[0,s -2 ]},{s,w,2},{t,0, 2 Pi},PlotStyle->Directive[Opacity[.2],Gray],Mesh->None, Lighting->"Neutral"],ParametricPlot3D[{(1-s/2) Cos[t],(1-s/2) Sin[t],Max[0,-s + 2 - w]},{s,w,2},{t,0, 2 Pi},PlotStyle->Directive[Opacity[.2],Gray],Mesh->None, Lighting->"Neutral"], 
ParametricPlot3D[{(1-s/2) Cos[t],(1-s/2) Sin[t],Min[0,s-2+ w]},{s,w,Min[2-(2^(2/3) (2 \[Pi]-Min[2Pi,3 V((w^2)/(.04))])^(1/3))/\[Pi]^(1/3)-w,2]},{t,0, 2 Pi},Mesh->None, PlotStyle->Directive[Opacity[1],Hue[a]], Lighting->"Neutral"],  ParametricPlot3D[{(w/2) Cos[t],(w/2) Sin[t], b},{t,0,2Pi}, {b, -2 + w, 0}, PlotStyle->Directive[Opacity[1], Hue[a]],Mesh->None, Lighting->"Neutral"],PlotRange->All,ImageSize->{300,300}, SphericalRegion-> True]},{Row[{Text["time to empty = "], Text[2Pi (.04)/(3w^2)],Text[" seconds"]}]}}],{start,ControlType->None},{end,ControlType->None},
{{V,.01,"time (seconds)"},0.01,34,.01,ControlType->Animator,AnimationRate->1,AnimationRunning->False,ImageSize->Small}, 
{{w,.05,"neck width (millimeters)"}, .05, .3,.01,Appearance->"Labeled"}, 
{{a,0,"color of sand"}, 0, 1,Appearance->"Labeled"}]

Источник: http://demonstrations.wolfram.com/FlowTimeInAnHourglass/

3

Источник

user97754 25 июн '15 в 11:39

Если это означает просто уровень представления, то это действительно зависит от результатов моделирования и представления, которое вы выбираете для него.

Например, если симуляция выводит одну переменную (например, объем одного из отсеков), то это может быть назначено непосредственно для атрибута визуализации, такого как расположение "верхней" крышки цилиндра. "Дополнительный" цилиндр может стоять поверх предыдущего с назначенными ему координатами нижней крышки (totalVolume-lowerCompartmentVolume).

В этом случае визуализация является всего лишь панелью мониторинга и не влияет на симуляцию (например, столкновения объектов или близость вообще не учитываются симуляцией).

Чтобы обобщить это, мы говорим о решении, в котором набор количеств назначен набору атрибутов визуализации.

С этой точки зрения, набор сложных объектов может быть создан с использованием VRML (или X3D), их атрибуты могут быть привязаны непосредственно к выходам моделирования, и рендеринг будет запускаться на каждом n-м временном шаге моделирования.

Чтобы создать "сцену" или объекты визуализации, вы можете использовать программное обеспечение, такое как blender, которое может экспортировать сцены VRML, или написать VRML вручную (это действительно простая задача).

С точки зрения инфраструктуры, MATLAB имеет инструментарий VRML, а Python имеет очень широкий выбор модулей, с помощью которых можно обрабатывать VRML (см., Например, эту и эту ссылку).

Для более конкретного примера:

Учитывая некоторые результаты моделирования y и файл шаблона VRML, как:

#VRML V2.0 utf8
Transform {
  translation 0 0 0
  children [
    Shape { geometry Box {2,2,zSize} }
  ]
}

Вы могли бы сделать что-то вроде:

data = (Read contents of VRML file as string data).
for n in [0..1000]:
    y = getSimulationOutput(aParameterVector)
    renderData = substitute(data, "zSize", y) #This function could be provided by a template module like jinja for example. 
    simulationFrame = renderVRML(renderData)
    saveImage(simulationFrame)

(Пожалуйста, обратите внимание: больше информации о Jinja можно найти здесь - комментируйте встроенную ссылку, не отображающуюся должным образом выше.)

Возвращаясь к файлу и привязывая различные элементы к разным количествам (например, изменяя преобразование, которое может вращать, масштабировать, перемещать блок или изменяя внешний вид блока, назначая другой цвет), вы можете создать любой вид " Панель инструментов "выход для вашей симуляции.... в том числе неправильных шестиугольников.

Этот метод является непосредственным применением документов, управляемых данными, но в другом месте (чем HTML или SVG).

Надеюсь это поможет.

2

Источник

user1301827 26 июн '15 в 08:35

Если ваша цель - визуализировать такие шестиугольники в Matlab, то fill а также fill3 должен сделать свое дело. Вот пример кода, который предполагает, что ваши шестиугольники параметризованы на две ширины w1 а также w2 и d1 а также d2 параметры, которые являются длинами сторон:

function draw_hexagon(w1, w2, d1, d2)
    a=(w1-w2)/2;
    b1=sqrt(d1^2 - a^2);
    b2=sqrt(d2^2 - a^2);

    xs=[-w1/2, w1/2, w2/2, w1/2, -w1/2, -w2/2];
    ys=[b1, b1, 0, -b2, -b2, 0];

    fill(xs, ys, 'b')
    axis square 
    grid on
end

Это произведет следующее для w1=4, w2=2, d1=2, d2=3:

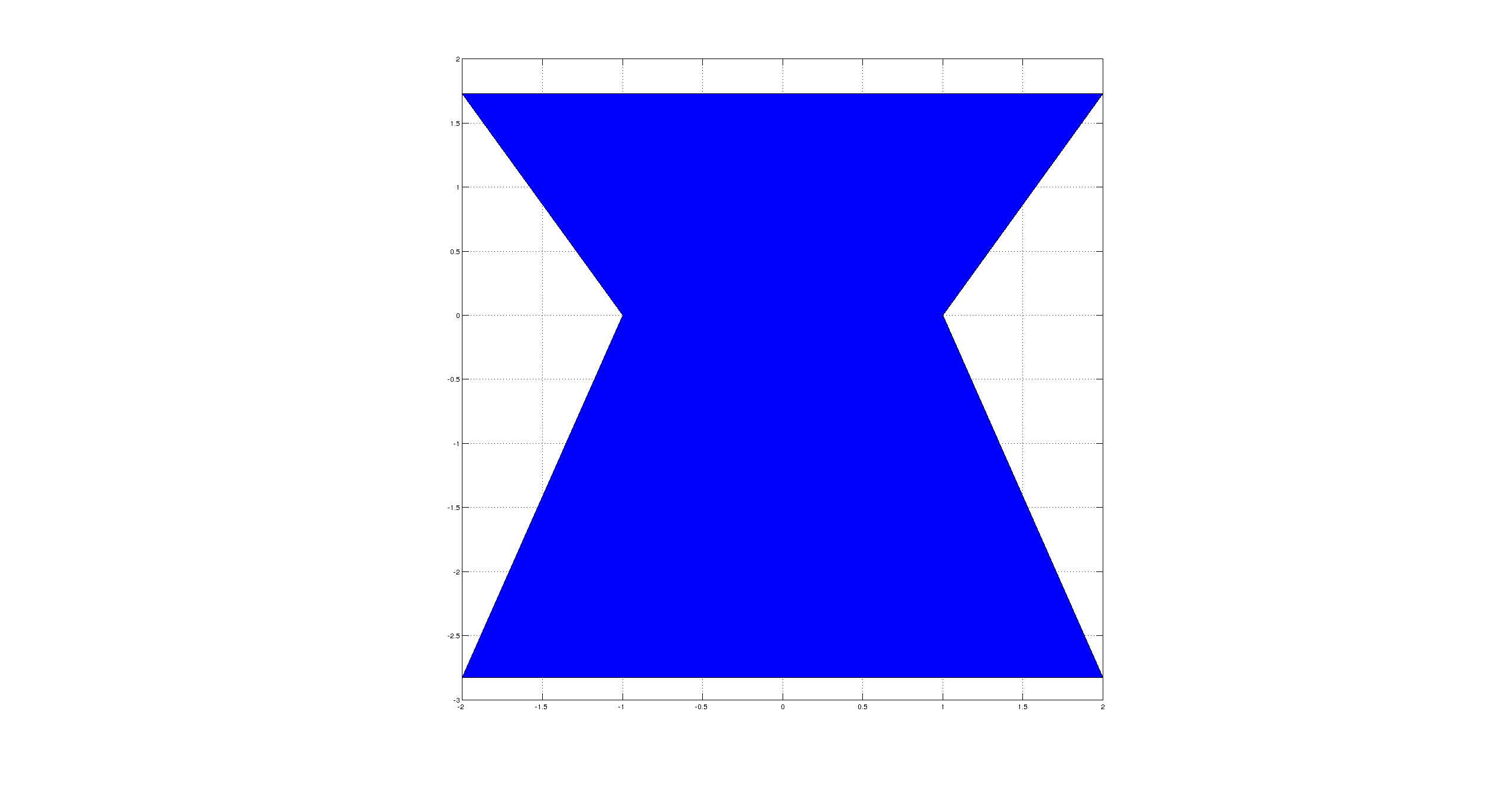
И аналогично для 3D:

function draw_hexagon_3d(w1, w2, d1, d2)
    a=(w1-w2)/2;
    b1=sqrt(d1^2 - a^2);
    b2=sqrt(d2^2 - a^2);

    xs=[-w1/2, w1/2, w2/2, w1/2, -w1/2, -w2/2];
    ys=[0, 0, 0, 0, 0, 0];
    zs=[b1, b1, 0, -b2, -b2, 0];

    fill3(xs, ys, zs, 'b')
    grid on
    axis square 
end

мы получаем:

2

Источник

user1576602 27 июн '15 в 06:25

Пытаясь установить стандартную библиотеку мешей, я считаю, что мы должны начать с определения степеней свободы.

Для вогнутых двухсимметричных шестиугольников с двумя горловинами это может быть:

ширина топора (W_m)
относительная ширина верха (w_t = W_t / W_m)
относительная ширина дна (w_b = W_b / W_m)
относительная высота
относительная высота дна

Ответы от Маргуса и А_А будут полезны для реализации.

1

Источник

user5047857 26 июн '15 в 21:25

Другие вопросы по тегам geometry mesh convex-optimization finite-element-analysis non-convex

user54964 29 июн '15 в 06:18 2015-06-29 06:18 · Accepted Answer · 2015-06-29 06:18

Я обсуждал этот вопрос с моей коллегой. Он мотивирует создать сеть треугольников, но также указывает общие алгоритмы для невыпуклых многоугольников.

Создать Mesh по собственному алгоритму

разделите шестиугольник на две трапеции по пунктирной линии, как показано в основной части вопроса
разделить трапеции на треугольники: assemmbly и построить триместные структуры inittri
вектор нагрузки f построен bilin_assembly (потому что это работало раньше, но не обязательно оптимальный выбор)

Разделение шестиугольника с двумя горловинами на две трапеции

возьмем два узла, у которых разность индексов равна трем, и какое расстояние наименьшее среди шести узлов.
образуют две трапеции, так что одна трапеция имеет номера 1-4, а другая 1,6,5,4.

Следующие синтаксисы основаны на моих редакциях кодов в 2013 году, но в основном на описаниях книги " Численные решения уравнений в частных производных методом конечных элементов " Клеса Джонсона.

Синтаксис ассемблера, где теперь рассматривается для простоты проблема Пуассона (должна быть уточнена здесь позже)

% [S,f]=assemblyGlobal(loadfunction,mesh)
%
%   loadfunction = function on the right-hand side of the Poisson equation
%   mesh         = mesh structure on which the assembly is done
%
%   S            = stiffness matrix of the Poisson problem
%   f            = load vector corresponding to loadfunction

где нам нужна билинейная сборка, синтаксис которой

% function B=bilin_assembly(bilin,mesh)
%
%  bilin = function handle to integrand of the bilinear form
%          given as bilin(u,v,ux,uy,vx,vy,x,y), where
%          u  - values of function u
%          v  - values of function v
%          ux - x-derivative of function u
%          uy - y-derivative of function u
%          vx - x-derivative of function v
%          vy - y-derivative of function v
%          x  - global x-coordinate
%          y  - global y-coordinate
%  mesh  = mesh structure on which the matrix will be assembled
%
%  B     = matrix related to bilinear form bilin

Синтаксис для инициации треугольной сетки

% function mesh = inittri(p,t)
%
%   p       = nodes
%   t       = triangles
%     
%   mesh    = trimesh structure corresponding to (p,t)
%
% TRIMESH STRUCTURE :
% 
%   p       = nodes in a 2xN-matrix
%
%   t       = triangles in a 3xN- matrix (nodes of the triangles as indeces to the p- matrix).
% 
%   edges   = a matrix of all edges in the mesh. Each column is an edge :
%             [n1 ; n2] where n1 < n2;
%
%   t2e     = a matrix connecting  triangle's and edges's. 
%             Each column corresponds to a triangle and has
%             triangle's edges in the order n1->n2, n2->n3,
%             n1->n3. 
%
%   e2t     = inverse of t2e.

Я не выкладывал здесь полные исходные коды из-за проблем с авторским правом, и они дадут ответ довольно долго. Однако все алгоритмы основаны на первом источнике, поэтому здесь может быть создан любой исследователь. Я думаю, что этот метод FEM - единственный способ найти здесь оптимальную сетку.

Алгоритмы для общих невыпуклых многоугольников

Существуют также алгоритмы, которые могут создавать сетки для общих невыпуклых многоугольников. Возможно, что сетка, предоставленная ответом Маргуса, получена таким алгоритмом.

Ansys

Я испытывал разные продукты о визуализации отверстий, разной геометрии и разных материалов. Ansys является многообещающим решением здесь.

источники

Численные решения уравнений в частных производных методом конечных элементов Клэса Джонсона.
Учебные записки по методам конечных элементов в моем университете, 2013-2014