Как найти правильное вращение от одного вектора к другому?
У меня есть два объекта, и у каждого объекта есть два вектора:
- нормальный вектор
- вверх вектор
Как на этом изображении:
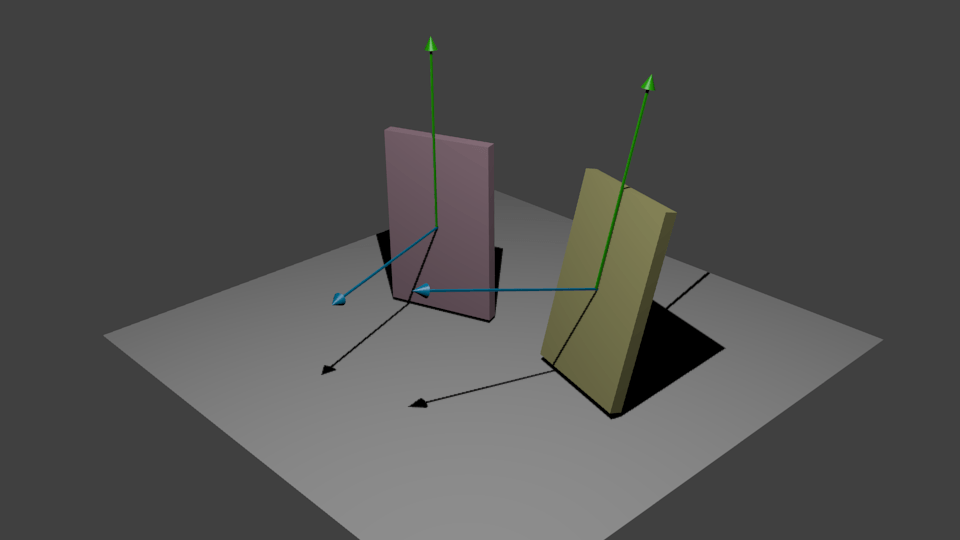
Вверх вектор перпендикулярен нормальному вектору. Теперь я хочу найти уникальное вращение от одного объекта к другому, как это сделать?
У меня есть один метод, чтобы найти вращение между одним вектором к другому, и это работает. Проблема в том, что мне нужно позаботиться о двух векторах: нормальном векторе и верхнем векторе. Если я использую этот метод, чтобы повернуть вектор нормали от объекта один к нормали от объекта два, вектор вверх мог бы указывать неправильный путь, и они должны быть параллельны.
Вот код для поиска кратчайшего поворота:
GE::Quat GE::Quat::fromTo(const Vector3 &v1, const Vector3 &v2)
{
Vector3 a = Vector3::cross(v1, v2);
Quat q;
float dot = Vector3::dot(v1, v2);
if ( dot >= 1 )
{
q = Quat(0,0,0,1);
}
else if ( dot < -0.999999 )
{
Vector3 axis = Vector3::cross(Vector3(1,0,0),v2);
if (axis.length() == 0) // pick another if colinear
axis = Vector3::cross(Vector3(0,1,0),v2);
axis.normalize();
q = Quat::axisToQuat(axis,180);
}
else
{
float s = sqrt( (1+dot)*2 );
float invs = 1 / s;
Vector3 c = Vector3::cross(v1, v2);
q.x = c.x * invs;
q.y = c.y * invs;
q.z = c.z * invs;
q.w = s * 0.5f;
}
q.normalize();
return q;
}
Что я должен изменить / добавить к этому коду, чтобы найти правильный поворот?
4 ответа
Прежде чем мы начнем, я предполагаю, что как вектор UP, так и вектор нормали нормализованы и ортогональны (скалярное произведение равно нулю) между ними.
Допустим, вы хотите повернуть свою желтую пластину, чтобы она совпала с розовой (красной?) Пластиной. Таким образом, нашей ссылкой будут векторы из желтой пластины, и мы будем называть нашу систему координат XYZ, где Z -> желтый нормальный вектор, Y -> желтый вектор Up и X -> YxZ (перекрестное произведение).
Таким же образом, для пластины розы повернутая система координат будет называться X'Y'Z', где Z' -> вектор нормальной розы, Y' -> вектор восходящей розы и X' -> Y'xZ' (перекрестное произведение).
Хорошо, чтобы найти матрицу вращения, нам нужно только убедиться, что наш нормальный желтый вектор станет вектором нормальной розы; что наш верхний желтый вектор будет преобразован в вектор восходящей розы и т. д., т. е.
RyellowTOrose = |X'x Y'x Z'x|
|X'y Y'y Z'y|
|X'z Y'z Z'z|
другими словами, после того, как у вас есть какие-либо примитивы, преобразованные в координаты желтой системы, применяя это преобразование, поверните его, чтобы выровнять с системой координат розы.
Если ваш верхний и нормальный вектор не являются ортогональными, вы можете легко исправить один из них. Просто сделайте перекрестное произведение между нормальным и верхним значениями (для удобства получается вектор с именем C) и повторите перекрестное произведение между C и нормальным, чтобы скорректировать вектор повышения.
Прежде всего, я утверждаю, что существует только одно такое преобразование, которое выровняет ориентацию двух объектов. Поэтому нам не нужно беспокоиться о поиске самого короткого.
Пусть объект, который будет вращаться, будет назван aи назовите объект, который остается неподвижным b, Позволять x а также y быть нормальными и восходящими векторами соответственно для aи так же пусть u а также v быть эти векторы для b, Я приду x, y, u, а также v единица длины, и это x ортогонально y, а также u ортогонально v, Если что-то из этого не так, может быть написан код дела, чтобы исправить это (посредством планарной проекции и нормализации).
Теперь давайте построим матрицы, определяющие "мировое пространство" ориентацию a а также b, (позволять ^ обозначим перекрестное произведение) построить z как x ^ yи построить c как a ^ b, Пишу x, y, z а также a, b, c чтобы столбцы каждой матрицы давали нам две матрицы, назовите их A а также B соответственно. (перекрестное произведение здесь дает нам единичную длину и взаимно ортогональный вектор, поскольку то же самое верно для операндов)
Изменение преобразования системы координат для получения B с точки зрения A является A^-1 (обратная матрица A, где ^ обозначает обобщение показателя степени), в данном случае A^-1 может быть вычислено как A^TПозади, так как A является ортогональной матрицей по построению. Затем физическое преобразование в B это просто матрица B сам. Таким образом, преобразование объекта A^-1а затем B даст желаемый результат. Однако эти преобразования могут быть объединены в одно преобразование путем умножения B справа в A^-1 налево.
В итоге вы получите эту матрицу (при условии отсутствия арифметических ошибок):
_ _
| x0*u0+x1*u1+x2*u2 x0*v0+x1*v1+x2*v2 x0*(u1*v2-u2*v1)+x1*(u2*v0-u0*v2)+x2*(u0*v1-u1*v0) |
| |
| y0*u0+y1*u1+y2*u2 y0*v0+y1*v1+y2*v2 y0*(u1*v2-u2*v1)+y1*(u2*v0-u0*v2)+y2*(u0*v1-u1*v0) |
| |
| (x0*y2-x2*y1)*u0+(x2*y0-x0*y2)*u1+(x0*y1-x1*y0)*u2 (x0*y2-x2*y1)*v0+(x2*y0-x0*y2)*v1+(x0*y1-x1*y0)*v2 (x0*y2-x2*y1)*(u1*v2-u2*v1)+(x2*y0-x0*y2)*(u2*v0-u0*v2)+(x0*y1-x1*y0)*(u0*v1-u1*v0) |
|_ _|
Код кватерниона вращает только один вектор в другой без вектора "вверх".
В вашем случае просто построить матрицу вращения из 3 ортогональных векторов
- нормализованный (единичный) вектор направления
- нормализованный вектор
- перекрестное произведение векторов направления и вверх.
Тогда у вас будет матрица R1 и R2 (3x3), представляющая вращение объекта в двух случаях.
Чтобы найти вращение от R1 до R2, просто сделайте
R1_to_R2 = R2 * R1.inversed()
И матрица R1_to_R2 является матрицей преобразования из одной ориентации в другую. ПРИМЕЧАНИЕ: R1.inversed() здесь можно заменить на R1.transposed()
Позвольте мне снова написать задачу, используя векторы, которые есть у вас на рисунке.
Проблема:
Допустим, у вас есть два вектора, blue_1 а также green_1 (они ортогональны), и вы ищете вращение, чтобы переместить эти векторы в blue_2 а также green_2 (они ортогональны). Более того, вы хотите green_2 быть параллельным green_1,
Решение:
Как я вижу, проблема здесь в том, что эти вращения существуют только в определенных ситуациях. Ваш вектор blue_2 должно быть уже ортогонально green_1, Если blue_2 не ортогонально green_1 ваше вращение не существует.
Зачем?
Позвольте R быть вращением, то есть
blue_2 = R*blue_1
green_2 = R*green_1
Мы знаем, что green_2 ортогонален blue_2, поэтому
dot(blue_2,green_2) = 0
Также green_2 и green_1 будут параллельными, только если они равны постоянному коэффициенту, отличному от нуля, скажем, aэто реальное число.
green_2 = a*green_1
Собрав все воедино, вы получите это
0 = dot(blue_2,green_2) = a*dot(blue_2,green_1)
потому что не ноль, мы получаем, что
dot(blue_2,green_1) = 0
Пример:
если ваши векторы
blue_1 = (1,0,0)
green_1 = (0,1,0)
и ваш новый вектор синий
blue_2 = (sqrt(2)/2,sqrt(2)/2,0)
тогда нет вероятности того, что вектор green_2 удовлетворяющие вашей ортогональности существуют, и тогда вы не найдете вращение, которое движется blue_1 но нет green_1,