Алгоритм растеризации и заполнения гиперсферы?
Я пытаюсь растеризовать и заполнить гиперсферу. По сути, у меня есть двумерная сетка фиксированного размера и сфера (центр, радиус), и я хочу выяснить, какие ячейки сетки перекрываются со сферой, и сохранить их координаты.
Мне известен алгоритм круга средней точки, который использует 8-стороннее зеркальное отображение и создает внешние ячейки (границу) круга. Я также изменил связанный код википедии, чтобы заполнить круг (то есть, чтобы получить координаты всех ячеек внутри границы).
Однако я не знаю никаких алгоритмов для более высокого измерения. Например, в 4d я думал о реализации путем создания всех возможных кругов, как в следующем псевдокоде. Основная идея состоит в том, что поскольку 4d сфера имеет вид (x-x0)2 + (y-y0) ** 2 + (z-z0) ** 2 + (k-k0) ** 2 = r2, это равно к (x-x0)2 + (y-y0) ** 2 = r2 - (z-z0) ** 2 - (k-k0) ** 2. Так как я знаю, как нарисовать круг, мне просто нужно создать все круги для всех возможных значений z и k.
assume center=(x0,y0,z0,k0) and radius r
for all dimensions equal or higher than 2://this is z and k
//make a list of possible values this dimension can take
//from z0 to z0+radius with a step of 1
all_lists.append([dim0,dim0+1,...,dim0+radius])
produce the product of all the lists in all_lists
//now i have a list [[z0,k0],[z0,k0+1],....,[z0+1,k0],[z0+1,k0+1],....,[z0+radius,k0],...[z0+radius,k0+radius]]
for every element l of the list, compute the radius of the circular "cut"
l.append(r**2 - z**2 - k**2)
Now call the Midpoint Circle Algorithm, but for every (x,y) pair that it produces, we need to export 4 points, namely (x,y,±z,±k)
Этот вопрос кажется актуальным, но я не понимаю ответа.
1 ответ
Ну, никто не отвечает в течение некоторого времени, поэтому вот мое простое и очевидное решение C++:
//---------------------------------------------------------------------------
const int N=10; // number of dimensions
struct point { double a[N]; }; // N-dimensional point
#define color DWORD // type of your color property
//---------------------------------------------------------------------------
// N x nested for(a=a0;a<=a1;a+=da) return false if ended
// it could be optimized a lot but for clarity I leve it as is
// ix=-1 at start and N = number of dimensions / nested count
bool nested_for(double *a0,double *a,double *a1,double *da,int &ix,int N)
{
if (ix<0)
{
int i;
if (N<1) return false; // N too low
for (i=0;i<N;i++) a[i]=a0[i];
for (i=0;i<N;i++) if (a[i]>a1[i]) return false; // a0>a1 for some i that is wrong !!!
ix=N-1;
return true;
}
for (;;) // a+=da
{
a[ix]+=da[ix];
if (a[ix]<=a1[ix]) break;
if (!ix) return false; // end of nested for
a[ix]=a0[ix];
ix--;
}
ix=N-1;
return true;
}
//---------------------------------------------------------------------------
void draw_point(point &p,color c)
{
// draw your point ...
}
//---------------------------------------------------------------------------
void fill_hypersphere(point &p0,double r,color c)
{
int i,ix;
bool init;
point a,b,a0,a1,da;
double aa,rr=r*r;
for (i=0;i<N;i++) a0.a[i]=-r; // loop boundary for all axises <-r,+r>
for (i=0;i<N;i++) a1.a[i]=+r;
for (i=0;i<N;i++) da.a[i]=1.0; // step between pixels
for (ix=-1;nested_for(a0.a,a.a,a1.a,da.a,ix,N);) // N x nested for
{
aa=0.0; // aa = distance from zero ^ 2
for (i=0;i<N;i++) aa+=a.a[i]*a.a[i];
if (aa<=rr) // if it is inside sphere
{ // compute the translated point by p0 to b
for (i=0;i<N;i++) b.a[i]=p0.a[i]+a.a[i];
draw_point(b,c); // and draw/fill it or whatever
}
}
}
//---------------------------------------------------------------------------
[Edit1] только что проведено тестирование
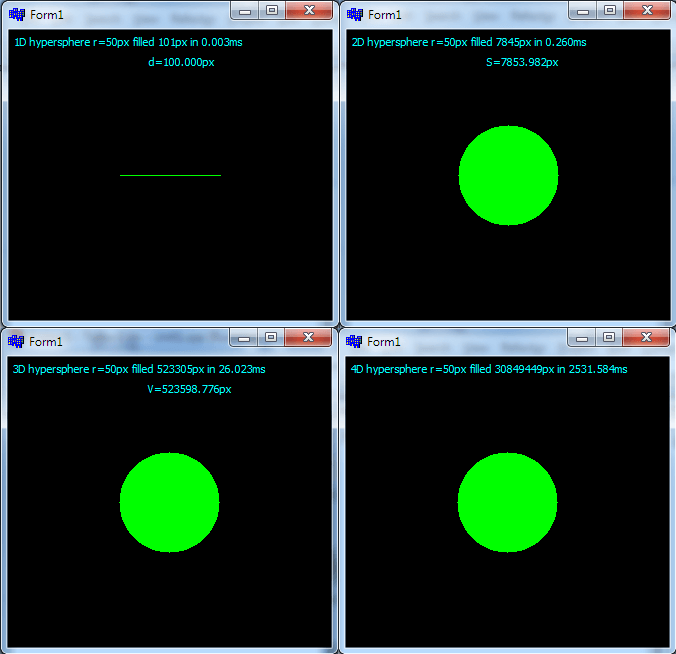
- это тестовое приложение для кода выше
- осмотр плоскости XY (z=0)
- для 1D,2D,3D и 4D гиперсфер
- Я не уверен насчет 1D, но все остальное в порядке (не уверен, что гиперпространство определено для 1D или должно быть только точкой)
- даже количество пикселей ~ Объем выглядит очень похоже, так что все должно быть в порядке
- помните, что сложность - это O(N!), где N - количество измерений
- и время выполнения = c0*(N!)*r, где c0 - постоянное время, r - радиус, а N - число измерений.