Фильтр Калмана для прогнозирования предыдущего шага из будущего

Question

Я новичок в фильтрах Калмана и пытаюсь использовать его для прогнозирования пропущенных значений, а также для получения сглаженных наблюдений по данным GPS (широта и долгота).

Я использую pykalman и мой блок кода выглядит следующим образом:

data = data[['Lat', 'Lon']]
measurements = np.asarray(data, dtype='float')
measurements_masked = np.ma.masked_invalid(measurements)

# initial state of the form  [x0, x0_dot, x1, x1_dot]
initial_state_mean = [
    measurements[0, 0],
    0,
    measurements[0, 1],
    0
]

initial_state_covariance = [[ 10, 0, 0, 0], 
                            [  0, 1, 0, 0],
                            [  0, 0, 1, 0],
                            [  0, 0, 0, 1]]

# transition matrix to estimate new position given old position
transition_matrix = [
    [1, 1, 0, 0],
    [0, 1, 0, 0],
    [0, 0, 1, 1],
    [0, 0, 0, 1]
]

observation_matrix = [
    [1, 0, 0, 0],
    [0, 0, 1, 0]
]

kf = KalmanFilter(
    transition_matrices=transition_matrix,
    observation_matrices=observation_matrix,
    initial_state_mean=initial_state_mean,
)

filtered_state_means = np.zeros((len(measurements), 4))
filtered_state_covariances = np.zeros((len(measurements), 4, 4))

for i in range(len(measurements)):
    if i == 0:
        filtered_state_means[i] = initial_state_mean
        filtered_state_covariances[i] = initial_state_covariance
    else:
        filtered_state_means[i], filtered_state_covariances[i] = (
        kf.filter_update(
            filtered_state_means[i-1],
            filtered_state_covariances[i-1],
            observation = measurements_masked[i])
        )

где данные - это фрейм данных Pandas, из которого извлекаются широта и долгота.

Правильна ли эта логика? Кроме того, я хочу сделать наблюдения, которые ближе к отсутствующим наблюдениям, чтобы предсказать пропущенные значения. Например, если в массиве из 10 выборок отсутствуют 5-е, 6-е и 7-е наблюдения, имеет смысл прогнозировать 5-е с использованием 4-й выборки, прогнозировать 7-е с использованием 8-й выборки и прогнозировать 6-е, беря в среднем 5-е и 7-е,

Имеет ли этот подход смысл? Если да, то как это сделать с помощью pykalman? Если нет, что можно сделать для более точного прогнозирования пропущенных значений при отсутствии большого количества последовательных значений в массиве?

Answer 1

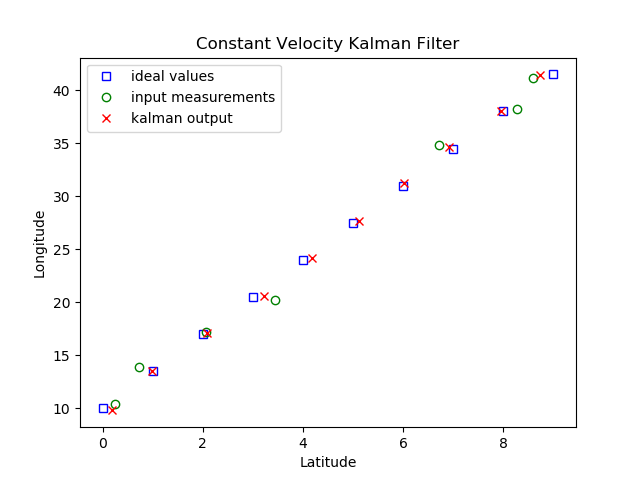
Я думаю, что фильтр Калмана отлично подходит для того, что вы хотите. Ниже приведен пример с некоторыми фиктивными данными, где я замаскировал (скрыл) некоторые выборки / измерения из фильтра. Как вы можете видеть, KF хорошо восстанавливает 3 точки, отсутствующие в середине. KF позаботится о том, чтобы наблюдения ближе к конкретной метке времени были наиболее важны для оценки этой метки времени (через предполагаемую динамику).

Это немного оптимистично, поскольку входные данные полностью соответствуют предположению, сделанному в KF (что объекты движутся с постоянной скоростью). Обратите внимание, что KF также должен хорошо работать, когда скорость действительно меняется. Я опубликовал предыдущий более длинный ответ на pykalman Библиотека здесь: /questions/36778539/kak-ispolzovat-filtr-kalmana-v-python-dlya-dannyih-o-mestopolozhenii/36778546#36778546, что может помочь в понимании того, как работает KF.

import numpy as np
import matplotlib.pyplot as plt
from pykalman import KalmanFilter

# Some dummy values, assume we're heading in straightline
# at constant speed
lat_ideal = np.array(range(10))
lon_ideal = np.array(lat_ideal*3.5 + 10)

lat = lat_ideal + np.random.uniform(-0.5, 0.5, 10)
lon = lon_ideal + np.random.uniform(-0.5, 0.5, 10)

# Assing some indexes as missing
measurementMissingIdx = [False, False, False, False, True, True, True, False, False, False]

# Create the starte measurement matrix and mark some of the time-steps
# (rows) as missing (masked)
measurements = np.ma.asarray([lat, lon]).transpose()
measurements[measurementMissingIdx] = np.ma.masked

# Kalman filter settings:
# state vector is [lat, lat_dot, lon, lon_dot]
Transition_Matrix=[[1,1,0,0],[0,1,0,0],[0,0,1,1],[0,0,0,1]]
Observation_Matrix=[[1,0,0,0],[0,0,1,0]]

initial_state_mean = [measurements[0, 0], 0,
                      measurements[0, 1], 0]

kf=KalmanFilter(transition_matrices=Transition_Matrix,
            observation_matrices =Observation_Matrix,
            em_vars=['initial_state_covariance', 'initial_state_mean'
                     'transition_covariance', 'observation_covariance'])

kf.em(measurements, n_iter=5)

# Increase observation co-variance
kf.observation_covariance = kf.observation_covariance*10

(smoothed_state_means, smoothed_state_covariances) = kf.smooth(measurements)

plt.plot(lat_ideal,lon_ideal,'sb', label='ideal values', markerfacecolor='none')
plt.plot(measurements[:,0],measurements[:,1],'og',label='input measurements', markerfacecolor='none')
plt.plot(smoothed_state_means[:,0],smoothed_state_means[:,2],'xr',label='kalman output')

plt.xlabel("Latitude")
plt.ylabel("Longitude")
legend = plt.legend(loc=2)
plt.title("Constant Velocity Kalman Filter")
plt.show()

Который производит график ниже: