Как использовать фильтр Калмана в Python для данных о местоположении?
[EDIT] Ответ @Claudio дает мне действительно хороший совет о том, как отфильтровывать выбросы. Я действительно хочу начать использовать фильтр Калмана на моих данных, хотя. Таким образом, я изменил приведенные ниже примеры данных, чтобы они имели едва различимые вариационные шумы, которые не настолько экстремальны (что я часто вижу) Если бы кто-нибудь еще мог дать мне какое-то руководство о том, как использовать PyKalman в моих данных, это было бы здорово. [/РЕДАКТИРОВАТЬ]
Для проекта робототехники я пытаюсь отследить воздушного змея с помощью камеры. Я программирую на Python, и я вставил ниже несколько шумных результатов поиска местоположения (каждый элемент также содержит объект datetime, но я оставил их для ясности).
[ # X Y
{'loc': (399, 293)},
{'loc': (403, 299)},
{'loc': (409, 308)},
{'loc': (416, 315)},
{'loc': (418, 318)},
{'loc': (420, 323)},
{'loc': (429, 326)}, # <== Noise in X
{'loc': (423, 328)},
{'loc': (429, 334)},
{'loc': (431, 337)},
{'loc': (433, 342)},
{'loc': (434, 352)}, # <== Noise in Y
{'loc': (434, 349)},
{'loc': (433, 350)},
{'loc': (431, 350)},
{'loc': (430, 349)},
{'loc': (428, 347)},
{'loc': (427, 345)},
{'loc': (425, 341)},
{'loc': (429, 338)}, # <== Noise in X
{'loc': (431, 328)}, # <== Noise in X
{'loc': (410, 313)},
{'loc': (406, 306)},
{'loc': (402, 299)},
{'loc': (397, 291)},
{'loc': (391, 294)}, # <== Noise in Y
{'loc': (376, 270)},
{'loc': (372, 272)},
{'loc': (351, 248)},
{'loc': (336, 244)},
{'loc': (327, 236)},
{'loc': (307, 220)}
]
Сначала я подумал о том, чтобы вручную вычислить выбросы, а затем просто удалить их из данных в режиме реального времени. Затем я прочитал о фильтрах Калмана и о том, как они специально предназначены для сглаживания зашумленных данных. Поэтому после некоторых поисков я нашел библиотеку PyKalman, которая, кажется, идеально подходит для этого. Так как я был немного потерян во всей терминологии фильтра Калмана, я прочитал вики и некоторые другие страницы фильтров Калмана. Я получил общее представление о фильтре Калмана, но я действительно потерян в том, как я должен применить его к своему коду.
В документации PyKalman я нашел следующий пример:
>>> from pykalman import KalmanFilter
>>> import numpy as np
>>> kf = KalmanFilter(transition_matrices = [[1, 1], [0, 1]], observation_matrices = [[0.1, 0.5], [-0.3, 0.0]])
>>> measurements = np.asarray([[1,0], [0,0], [0,1]]) # 3 observations
>>> kf = kf.em(measurements, n_iter=5)
>>> (filtered_state_means, filtered_state_covariances) = kf.filter(measurements)
>>> (smoothed_state_means, smoothed_state_covariances) = kf.smooth(measurements)
Я просто заменил наблюдения своими наблюдениями следующим образом:
from pykalman import KalmanFilter
import numpy as np
kf = KalmanFilter(transition_matrices = [[1, 1], [0, 1]], observation_matrices = [[0.1, 0.5], [-0.3, 0.0]])
measurements = np.asarray([(399,293),(403,299),(409,308),(416,315),(418,318),(420,323),(429,326),(423,328),(429,334),(431,337),(433,342),(434,352),(434,349),(433,350),(431,350),(430,349),(428,347),(427,345),(425,341),(429,338),(431,328),(410,313),(406,306),(402,299),(397,291),(391,294),(376,270),(372,272),(351,248),(336,244),(327,236),(307,220)])
kf = kf.em(measurements, n_iter=5)
(filtered_state_means, filtered_state_covariances) = kf.filter(measurements)
(smoothed_state_means, smoothed_state_covariances) = kf.smooth(measurements)
но это не дает мне никаких значимых данных. Например, smoothed_state_means становится следующим:
>>> smoothed_state_means
array([[-235.47463353, 36.95271449],
[-354.8712597 , 27.70011485],
[-402.19985301, 21.75847069],
[-423.24073418, 17.54604304],
[-433.96622233, 14.36072376],
[-443.05275258, 11.94368163],
[-446.89521434, 9.97960296],
[-456.19359012, 8.54765215],
[-465.79317394, 7.6133633 ],
[-474.84869079, 7.10419182],
[-487.66174033, 7.1211321 ],
[-504.6528746 , 7.81715451],
[-506.76051587, 8.68135952],
[-510.13247696, 9.7280697 ],
[-512.39637431, 10.9610031 ],
[-511.94189431, 12.32378146],
[-509.32990832, 13.77980587],
[-504.39389762, 15.29418648],
[-495.15439769, 16.762472 ],
[-480.31085928, 18.02633612],
[-456.80082586, 18.80355017],
[-437.35977492, 19.24869224],
[-420.7706184 , 19.52147918],
[-405.59500937, 19.70357845],
[-392.62770281, 19.8936389 ],
[-388.8656724 , 20.44525168],
[-361.95411607, 20.57651509],
[-352.32671579, 20.84174084],
[-327.46028214, 20.77224385],
[-319.75994982, 20.9443245 ],
[-306.69948771, 21.24618955],
[-287.03222693, 21.43135098]])
Может ли более яркая душа, чем я, дать мне несколько подсказок или примеров в правильном направлении? Все советы приветствуются!
2 ответа
TL;DR, см. Код и рисунок внизу.
Я думаю, что фильтр Калмана может хорошо работать в вашем приложении, но он потребует немного больше думать о динамике / физике кайта.
Я настоятельно рекомендую прочитать эту страницу. Я не имею никакого отношения к автору или не знаю его автора, но я потратил около суток, пытаясь разобраться с фильтрами Калмана, и эта страница действительно заставила меня щелкнуть.
Кратко; для системы, которая является линейной и которая имеет известную динамику (то есть, если вы знаете состояние и входные данные, вы можете предсказать будущее состояние), она обеспечивает оптимальный способ объединения того, что вы знаете о системе, для оценки ее истинного состояния. Умный бит (о котором заботится вся матричная алгебра, которую вы видите на страницах, ее описывающих) - это то, как она оптимально объединяет две части вашей информации:
Измерения (которые подвержены "шуму измерения", т.е. датчики не совершенны)
Динамика (т. Е. То, как вы полагаете, что состояния развиваются в зависимости от входных данных, которые подвержены "технологическому шуму", а это просто способ сказать, что ваша модель не соответствует реальности).
Вы указываете, насколько вы уверены в каждом из них (через матрицы ковариаций R и Q соответственно), а коэффициент усиления Калмана определяет, насколько вы должны верить своей модели (т.е. вашей текущей оценке вашего состояния), и насколько вы должны поверь своим измерениям.
Без лишних слов давайте создадим простую модель вашего воздушного змея. Ниже я предлагаю очень простую возможную модель. Возможно, вы знаете больше о динамике воздушного змея, поэтому можете создать лучшую.
Давайте рассматривать кайт как частицу (очевидно, упрощение, настоящий кайт - это расширенное тело, поэтому имеет ориентацию в 3 измерениях), который имеет четыре состояния, которые для удобства мы можем записать в векторе состояний:
x = [x, x_dot, y, y_dot],
Где x и y - позиции, а _dot - скорости в каждом из этих направлений. Исходя из вашего вопроса, я предполагаю, что есть два (потенциально шумных) измерения, которые мы можем записать в вектор измерений:
z = [x, y],
Мы можем записать измерительную матрицу ( здесь обсуждается H, и observation_matrices в pykalman библиотека):
z = H x => H = [[1, 0, 0, 0], [0, 0, 1, 0]]
Затем нам нужно описать динамику системы. Здесь я буду предполагать, что никакие внешние силы не действуют, и что нет движения демпфирования кайта (с большим количеством знаний вы сможете добиться большего успеха, это эффективно рассматривает внешние силы и демпфирование как неизвестное / не смоделированное нарушение).
В этом случае динамика для каждого из наших состояний в текущей выборке "k" как функция состояний в предыдущих выборках "k-1" задается как:
x (k) = x (k-1) + dt * x_dot (k-1)
x_dot (k) = x_dot (k-1)
y (k) = y (k-1) + dt * y_dot (k-1)
y_dot (k) = y_dot (k-1)
Где "dt" - шаг по времени. Мы предполагаем, что (x, y) позиция обновляется на основе текущей позиции и скорости, а скорость остается неизменной. Учитывая, что единицы не заданы, мы можем просто сказать, что единицы скорости таковы, что мы можем опустить "dt" в приведенных выше уравнениях, то есть в единицах измерения position_units/sample_interval (я предполагаю, что ваши измеренные выборки находятся на постоянном интервале). Мы можем суммировать эти четыре уравнения в матрицу динамики как (F обсуждается здесь, и transition_matrices в pykalman библиотека):
x(k) = Fx(k-1) => F = [[1, 1, 0, 0], [0, 1, 0, 0], [0, 0, 1, 1], [0, 0, 0, 1]].
Теперь мы можем попробовать использовать фильтр Калмана в python. Модифицировано из вашего кода:
from pykalman import KalmanFilter
import numpy as np
import matplotlib.pyplot as plt
import time
measurements = np.asarray([(399,293),(403,299),(409,308),(416,315),(418,318),(420,323),(429,326),(423,328),(429,334),(431,337),(433,342),(434,352),(434,349),(433,350),(431,350),(430,349),(428,347),(427,345),(425,341),(429,338),(431,328),(410,313),(406,306),(402,299),(397,291),(391,294),(376,270),(372,272),(351,248),(336,244),(327,236),(307,220)])
initial_state_mean = [measurements[0, 0],
0,
measurements[0, 1],
0]
transition_matrix = [[1, 1, 0, 0],
[0, 1, 0, 0],
[0, 0, 1, 1],
[0, 0, 0, 1]]
observation_matrix = [[1, 0, 0, 0],
[0, 0, 1, 0]]
kf1 = KalmanFilter(transition_matrices = transition_matrix,
observation_matrices = observation_matrix,
initial_state_mean = initial_state_mean)
kf1 = kf1.em(measurements, n_iter=5)
(smoothed_state_means, smoothed_state_covariances) = kf1.smooth(measurements)
plt.figure(1)
times = range(measurements.shape[0])
plt.plot(times, measurements[:, 0], 'bo',
times, measurements[:, 1], 'ro',
times, smoothed_state_means[:, 0], 'b--',
times, smoothed_state_means[:, 2], 'r--',)
plt.show()
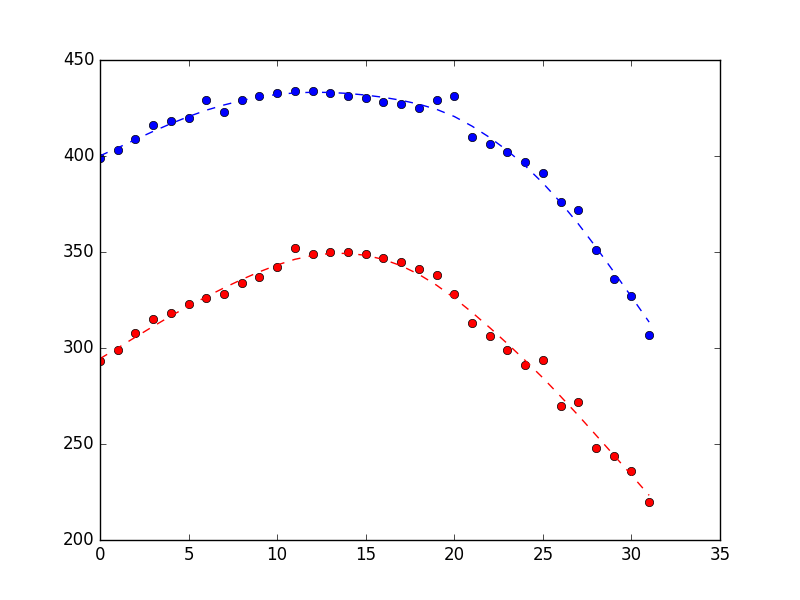
Это дало следующий результат, демонстрируя разумную работу по подавлению шума (синий - это позиция x, красный - позиция y, а ось x- просто номер выборки).
Предположим, вы смотрите на сюжет выше и думаете, что он выглядит слишком ухабистым. Как ты мог это исправить? Как обсуждалось выше, фильтр Калмана действует на две части информации:
- Измерения (в этом случае двух наших состояний, х и у)
- Динамика системы (и текущая оценка состояния)
Динамика, описанная в модели выше, очень проста. В буквальном смысле они говорят, что позиции будут обновляться текущими скоростями (очевидным, физически разумным образом), и что скорости остаются постоянными (это явно не физически верно, но отражает нашу интуицию о том, что скорости должны изменяться медленно).
Если мы считаем, что оценочное состояние должно быть более плавным, один из способов достижения этого состоит в том, чтобы сказать, что у нас меньше уверенности в наших измерениях, чем в нашей динамике (т.е. observation_covarianceотносительно нашего state_covariance).
Начиная с конца кода выше, исправьте observation covariance до 10-кратного значения, оцененного ранее, настройка em_vars как показано, требуется, чтобы избежать переоценки ковариации наблюдения (см. здесь)
kf2 = KalmanFilter(transition_matrices = transition_matrix,
observation_matrices = observation_matrix,
initial_state_mean = initial_state_mean,
observation_covariance = 10*kf1.observation_covariance,
em_vars=['transition_covariance', 'initial_state_covariance'])
kf2 = kf2.em(measurements, n_iter=5)
(smoothed_state_means, smoothed_state_covariances) = kf2.smooth(measurements)
plt.figure(2)
times = range(measurements.shape[0])
plt.plot(times, measurements[:, 0], 'bo',
times, measurements[:, 1], 'ro',
times, smoothed_state_means[:, 0], 'b--',
times, smoothed_state_means[:, 2], 'r--',)
plt.show()
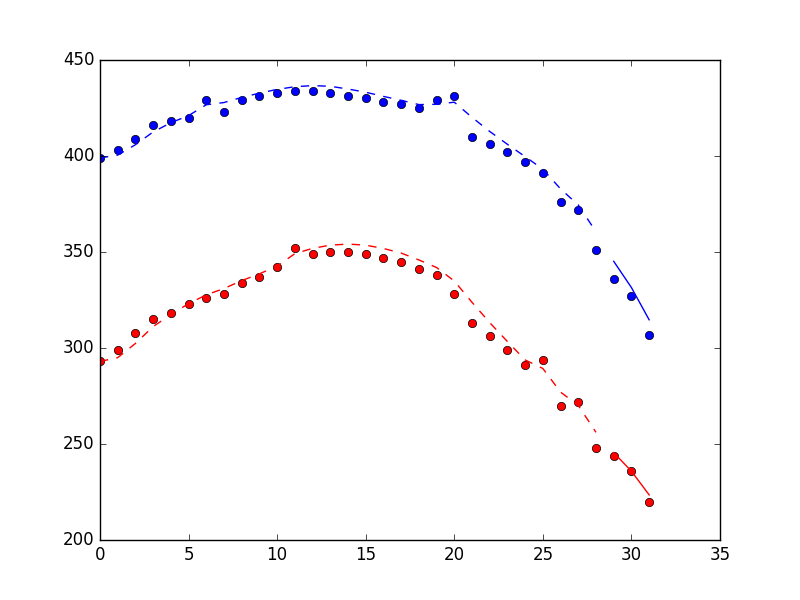
Который дает график ниже (измерения в виде точек, оценки состояния в виде пунктирной линии). Разница довольно тонкая, но, надеюсь, вы увидите, что она более гладкая.
Наконец, если вы хотите использовать этот встроенный фильтр в режиме онлайн, вы можете сделать это, используя filter_update метод. Обратите внимание, что это использует filter метод, а не smooth метод, потому что smooth метод может быть применен только к групповым измерениям. Больше здесь:
time_before = time.time()
n_real_time = 3
kf3 = KalmanFilter(transition_matrices = transition_matrix,
observation_matrices = observation_matrix,
initial_state_mean = initial_state_mean,
observation_covariance = 10*kf1.observation_covariance,
em_vars=['transition_covariance', 'initial_state_covariance'])
kf3 = kf3.em(measurements[:-n_real_time, :], n_iter=5)
(filtered_state_means, filtered_state_covariances) = kf3.filter(measurements[:-n_real_time,:])
print("Time to build and train kf3: %s seconds" % (time.time() - time_before))
x_now = filtered_state_means[-1, :]
P_now = filtered_state_covariances[-1, :]
x_new = np.zeros((n_real_time, filtered_state_means.shape[1]))
i = 0
for measurement in measurements[-n_real_time:, :]:
time_before = time.time()
(x_now, P_now) = kf3.filter_update(filtered_state_mean = x_now,
filtered_state_covariance = P_now,
observation = measurement)
print("Time to update kf3: %s seconds" % (time.time() - time_before))
x_new[i, :] = x_now
i = i + 1
plt.figure(3)
old_times = range(measurements.shape[0] - n_real_time)
new_times = range(measurements.shape[0]-n_real_time, measurements.shape[0])
plt.plot(times, measurements[:, 0], 'bo',
times, measurements[:, 1], 'ro',
old_times, filtered_state_means[:, 0], 'b--',
old_times, filtered_state_means[:, 2], 'r--',
new_times, x_new[:, 0], 'b-',
new_times, x_new[:, 2], 'r-')
plt.show()
График ниже показывает эффективность метода фильтрации, включая 3 точки, найденные с использованием filter_update метод. Точки - это измерения, пунктирная линия - оценки состояния для периода обучения фильтра, сплошная линия - оценки состояния для периода "онлайн".
И информация о времени (на моем ноутбуке).
Time to build and train kf3: 0.0677888393402 seconds
Time to update kf3: 0.00038480758667 seconds
Time to update kf3: 0.000465154647827 seconds
Time to update kf3: 0.000463008880615 seconds
Из того, что я вижу, использование фильтрации Калмана, возможно, не является правильным инструментом в вашем случае.
Как насчет этого?:
lstInputData = [
[346, 226 ],
[346, 211 ],
[347, 196 ],
[347, 180 ],
[350, 2165], ## noise
[355, 154 ],
[359, 138 ],
[368, 120 ],
[374, -830], ## noise
[346, 90 ],
[349, 75 ],
[1420, 67 ], ## noise
[357, 64 ],
[358, 62 ]
]
import pandas as pd
import numpy as np
df = pd.DataFrame(lstInputData)
print( df )
from scipy import stats
print ( df[(np.abs(stats.zscore(df)) < 1).all(axis=1)] )
Вот вывод:
0 1
0 346 226
1 346 211
2 347 196
3 347 180
4 350 2165
5 355 154
6 359 138
7 368 120
8 374 -830
9 346 90
10 349 75
11 1420 67
12 357 64
13 358 62
0 1
0 346 226
1 346 211
2 347 196
3 347 180
5 355 154
6 359 138
7 368 120
9 346 90
10 349 75
12 357 64
13 358 62
Смотрите здесь для получения дополнительной информации и источника, из которого я получил код выше.