Подгонка окружности Python к точкам данных, менее чувствительным к случайному шуму
У меня есть набор измеренных радиусов (t+ эпсилон + ошибка) под одинаково разнесенными углами. Модель представляет собой круг радиуса (R) с центром в (r, альфа) с добавленным небольшим шумом и некоторыми случайными значениями ошибок, которые намного больше, чем шум.
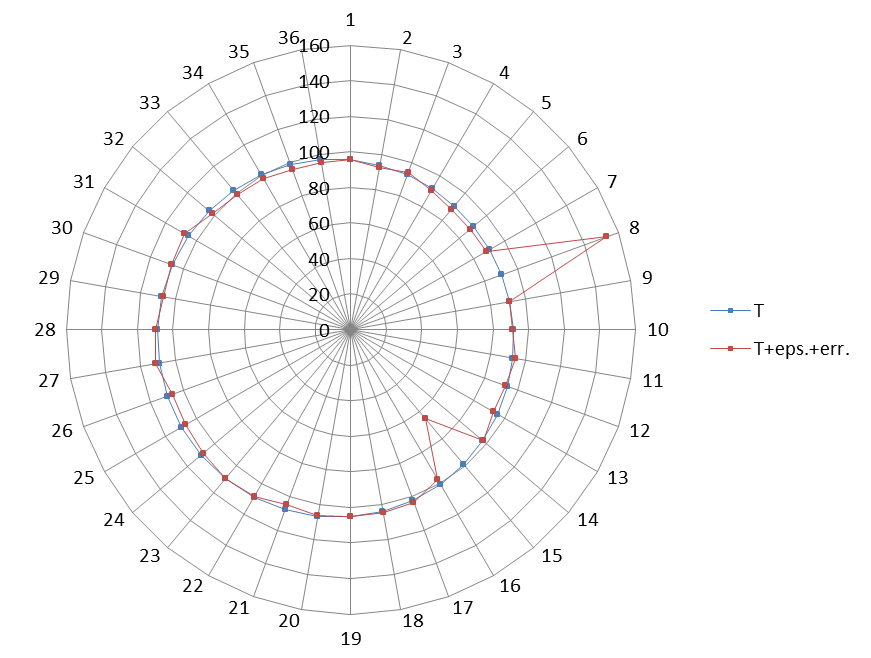
Задача состоит в том, чтобы найти центр модели круга (r, альфа) и радиус круга (R). Но он не должен быть слишком чувствительным к случайным ошибкам (в нижних точках данных на 7 и 14).
Некоторые радиусы могут отсутствовать, поэтому простое среднее здесь не сработает.
Я попробовал наименьшую квадратную оптимизацию, но она значительно реагирует на ошибки.
Есть ли способ оптимизации наименьших дельт, но не наименьших квадратов дельты в Python?
Model:
n=36
R=100
r=10
Alpha=2*Pi/6
Data points:
[95.85, 92.66, 94.14, 90.56, 88.08, 87.63, 88.12, 152.92, 90.75, 90.73, 93.93, 92.66, 92.67, 97.24, 65.40, 97.67, 103.66, 104.43, 105.25, 106.17, 105.01, 108.52, 109.33, 108.17, 107.10, 106.93, 111.25, 109.99, 107.23, 107.18, 108.30, 101.81, 99.47, 97.97, 96.05, 95.29]
2 ответа
Отвечая на ваш последний вопрос
Есть ли способ оптимизации наименьших дельт, но не наименьших квадратов дельты в Python?
Да, выберите метод оптимизации (например, скоростной спуск, реализованный в scipy.optimize.fmin) и использовать сумму абсолютных отклонений в качестве оценочной функции. Ваш набор данных мал, я полагаю, что любой метод оптимизации общего назначения будет быстро сходиться. (В случае нелинейного подбора наименьших квадратов также можно использовать алгоритм оптимизации общего назначения, но более распространенным является алгоритм Левенберга-Марквардта, который минимизирует суммы квадратов.)
Если вы заинтересованы в том, чтобы сведение к минимуму абсолютных отклонений вместо квадратов имело теоретическое обоснование, см. " Численные рецепты", глава " Надежная оценка".
С практической стороны сумма абсолютных отклонений может не иметь единственного минимума. В тривиальном случае двух точек, скажем, (0,5) и (1,9) и постоянной функции y = a, любое значение от 5 до 9 дает одинаковую сумму (4). Нет такой проблемы, когда отклонения возводятся в квадрат.
Если минимизация абсолютных отклонений не будет работать, вы можете рассмотреть эвристическую процедуру для выявления и устранения выбросов. Такие как RANSAC или ROUT.
Похоже, что вашей главной проблемой здесь будет удаление выбросов. Есть несколько способов сделать это, но для вашего приложения лучше всего просто удалить элементы на основе их расстояния от медианы (поскольку медиана гораздо менее чувствительна к выбросам, чем средняя).
Если вы используете numpy это будет выглядеть так:
def remove_outliers(data_points, margin=1.5):
nd = np.abs(data_points - np.median(data_points))
s = nd/np.median(nd)
return data_points[s<margin]
После чего вы должны запустить наименьших квадратов.
Если вы не используете numpy вы можете сделать что-то подобное с родными списками Python:
def median(points):
return sorted(points)[len(points)/2] # evaluates to an int in python2
def remove_outliers(data_points, margin=1.5):
m = median(data_points)
centered_points = [abs(point - m) for point in data_points]
centered_median = median(centered_points)
ratios = [datum/centered_median for datum in centered_points]
return [point for i, point in enumerate(data_points) if ratios[i]>margin]
Если вы просто не рассчитываете выбросы так высоко, вы можете просто рассчитать среднее значение вашего набора данных, который является просто линейным эквивалентом оптимизации наименьших квадратов.
Если вы ищете что-то получше, я мог бы предложить пропустить ваши данные через какой-то фильтр нижних частот, но я не думаю, что это действительно нужно здесь.
Фильтр нижних частот, вероятно, будет лучшим, что вы можете сделать следующим образом: (Обратите внимание, альфа - это число, с которым вам нужно будет поиграться, чтобы получить желаемый результат.)
def low_pass(data, alpha):
new_data = [data[0]]
for i in range(1, len(data)):
new_data.append(alpha * data[i] + (1 - alpha) * new_data[i-1])
return new_data
В этот момент ваша оптимизация наименьших квадратов должна работать нормально.