Очень высокая остаточная сумма квадратов

Question

У меня проблема с квадратной суммой остатков фитинга. Квадратная сумма остатков слишком высока, что указывает на то, что подгонка не очень хорошая. Тем не менее, визуально это выглядит хорошо, имея такую ​​высокую остаточную стоимость... Может кто-нибудь помочь мне узнать, что происходит?

Мои данные:

x=c(0.017359, 0.019206, 0.020619, 0.021022, 0.021793, 0.022366, 0.025691, 0.025780, 0.026355, 0.028858, 0.029766, 0.029967, 0.030241, 0.032216, 0.033657,
 0.036250, 0.039145, 0.040682, 0.042334, 0.043747, 0.044165, 0.044630, 0.046045, 0.048138, 0.050813, 0.050955, 0.051910, 0.053042, 0.054853, 0.056886,
0.058651, 0.059472, 0.063770,0.064567, 0.067415, 0.067802, 0.068995, 0.070742,0.073486, 0.074085 ,0.074452, 0.075224, 0.075853, 0.076192, 0.077002,
 0.078273, 0.079376, 0.083269, 0.085902, 0.087619, 0.089867, 0.092606, 0.095944, 0.096327, 0.097019, 0.098444, 0.098868, 0.098874, 0.102027, 0.103296,
 0.107682, 0.108392, 0.108719, 0.109184, 0.109623, 0.118844, 0.124023, 0.124244, 0.129600, 0.130892, 0.136721, 0.137456, 0.147343, 0.149027, 0.152818,
0.155706,0.157650, 0.161060, 0.162594, 0.162950, 0.165031, 0.165408, 0.166680, 0.167727, 0.172882, 0.173264, 0.174552,0.176073, 0.185649, 0.194492,
 0.196429, 0.200050, 0.208890, 0.209826, 0.213685, 0.219189, 0.221417, 0.222662, 0.230860, 0.234654, 0.235211, 0.241819, 0.247527, 0.251528, 0.253664,
 0.256740, 0.261723, 0.274585, 0.278340, 0.281521, 0.282332, 0.286166, 0.288103, 0.292959, 0.295201, 0.309456, 0.312158, 0.314132, 0.319906, 0.319924,
 0.322073, 0.325427, 0.328132, 0.333029, 0.334915, 0.342098, 0.345899, 0.345936, 0.350355, 0.355015, 0.355123, 0.356335, 0.364257, 0.371180, 0.375171,
0.377743, 0.383944, 0.388606, 0.390111, 0.395080, 0.398209, 0.409784, 0.410324, 0.424782 )


y= c(34843.40, 30362.66, 27991.80 ,28511.38, 28004.74, 27987.13, 22272.41, 23171.71, 23180.03, 20173.79, 19751.84, 20266.26, 20666.72, 18884.42, 17920.78, 15980.99, 14161.08, 13534.40, 12889.18, 12436.11,
12560.56, 12651.65, 12216.11, 11479.18, 10573.22, 10783.99, 10650.71, 10449.87, 10003.68,  9517.94,  9157.04,  9104.01,  8090.20,  8059.60,  7547.20,  7613.51,  7499.47,  7273.46,  6870.20,  6887.01,
6945.55,  6927.43,  6934.73,  6993.73,  6965.39,  6855.37,  6777.16,  6259.28,  5976.27,  5835.58,  5633.88,  5387.19,  5094.94,  5129.89,  5131.42,  5056.08,  5084.47,  5155.40,  4909.01,  4854.71,
4527.62,  4528.10,  4560.14,  4580.10,  4601.70,  3964.90,  3686.20,  3718.46,  3459.13,  3432.05,  3183.09,  3186.18,  2805.15,  2773.65,  2667.73,  2598.55,  2563.02,  2482.63,  2462.49,  2478.10,
2441.70,  2456.16,  2444.00,  2438.47,  2318.64,  2331.75,  2320.43,  2303.10,  2091.95,  1924.55, 1904.91,  1854.07,  1716.52,  1717.12,  1671.00,  1602.70,  1584.89,  1581.34,  1484.16,  1449.26,
1455.06,  1388.60,  1336.71,  1305.60,  1294.58,  1274.36,  1236.51,  1132.67,  1111.35,  1095.21,  1097.71,  1077.05,  1071.04,  1043.99,  1036.22,   950.26,   941.06,   936.37,   909.72,   916.45,
911.01, 898.94,   890.68,   870.99,   867.45,   837.39,   824.93,   830.61,   815.49,   799.77,   804.84,   804.88,   775.53,   751.95,   741.01,   735.86,   717.03,   704.57,   703.74,   690.63,
684.24,   650.30,   652.74,   612.95 )

Затем выполните подгонку с помощью функции nlsLM (пакет minpack.lm):

library(magicaxis)
library(minpack.lm)

sig.backg=3*10^(-3) 

mod <- nlsLM(y ~ a *( 1 + (x/b)^2 )^c+sig.backg,
             start = c(a = 0, b = 1, c = 0),
             trace = TRUE)

## plot data
magplot(x, y, main = "data", log = "xy", pch=16)
## plot fitted values
lines(x, fitted(mod), col = 2, lwd = 4 )

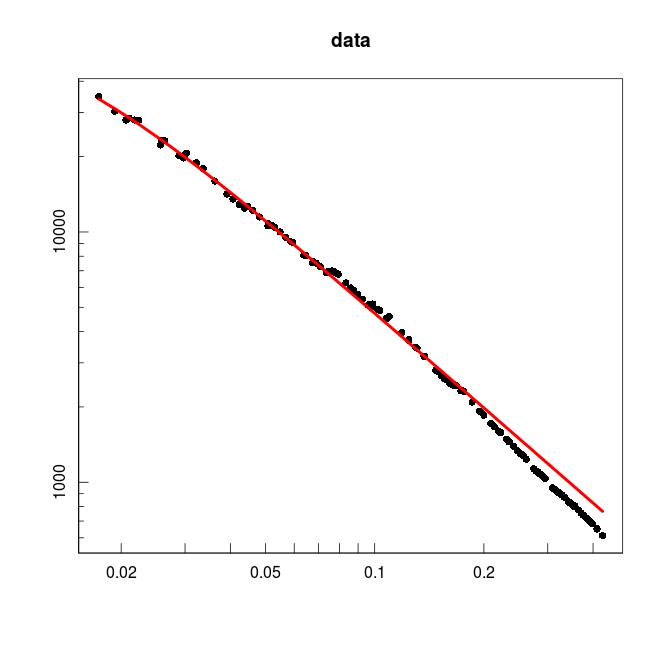
Это значение является остатком:

> print(mod)
Nonlinear regression model
  model: y ~ a * (1 + (x/b)^2)^c + sig.backg
   data: parent.frame()
         a          b          c 
68504.2013     0.0122    -0.6324 
 residual sum-of-squares: 12641435

Number of iterations to convergence: 34 
Achieved convergence tolerance: 0.0000000149

Остаток суммы квадратов слишком высок: 12641435 ...

Это так или что-то не так с настройкой? Это плохо?

Answer 1

Это имеет смысл, поскольку среднеквадратичное значение вашей переменной ответа равно 38110960. Вы можете масштабировать свои данные, если предпочитаете работать с меньшими числами.

Answer 2

Остаточная сумма квадратов не имеет большого значения, если не знать общую сумму квадратов (из которой можно рассчитать R^2). Его значение будет увеличиваться, если ваши данные имеют большие значения или если вы добавите больше точек данных, независимо от того, насколько хорошо вы подходите. Кроме того, вы можете захотеть взглянуть на график зависимости ваших остатков от подгоночных данных, и ваша модель должна объяснить эту модель, чтобы обеспечить нормальное распределение ошибок.